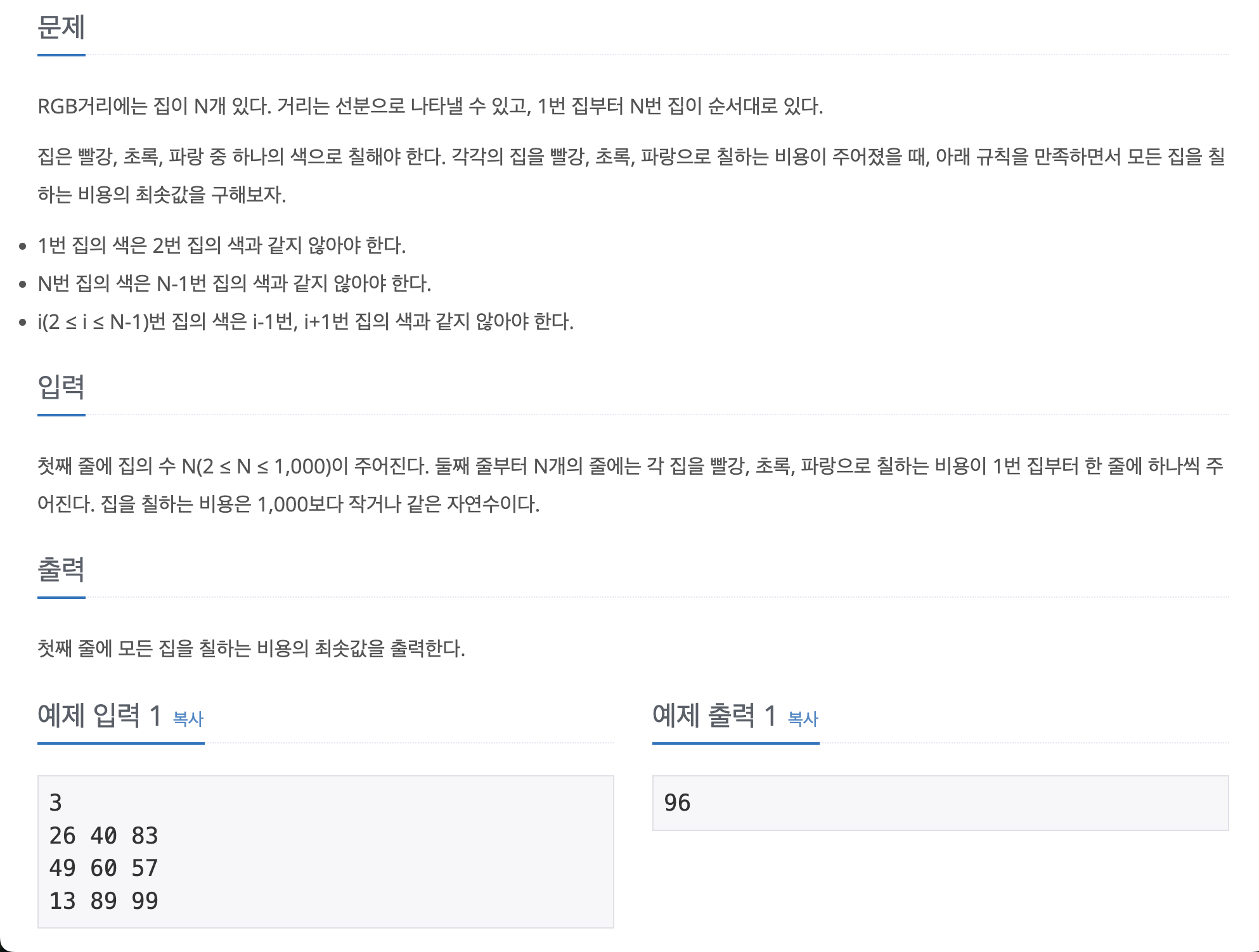
문제 출처 : https://www.acmicpc.net/problem/1149

---

문제 파악

직관적으로 그리디 전략

"매 집에서 가장 싼 색 고르자."

를 생각할 수 있다. 그러나

문제는 이 선택이 뒤에서 더 큰 비용을 강제로 만들 수 있다는 점이다.

예를 들어 앞에서 빨강이 싸서 칠했는데,
다음 집들에서 빨강이 너무 비싸거나 색 제한 때문에 선택지가 좁아져
전체 비용이 더 커질 수 있다.

즉,

• 그리디 = 지금만 보고 결정 → 미래 영향 고려 X
• 그래서 전체 최소가 보장되지 않는다.

---

그러나 이 문제는 DP를 활용해 풀어야 한다.

DP는 “가능한 모든 색 선택에 대한 최소 비용”을 동시에 관리한다.

핵심 아이디어:

i번 집을 R/G/B 중 어떤 색으로 칠했을 때의 최소 비용을 각각 저장한다.

즉,
i번 집을 R로 끝낸 경우의 최소
i번 집을 G로 끝낸 경우의 최소
i번 집을 B로 끝낸 경우의 최소
이 세 가지를 전부 들고 다음 집으로 간다.

그래서 앞에서 R이 싸다고 R만 선택하고 가두지 않는다.
모든 색에 대한 “최소 경로”를 끝까지 유지하니까
뒤에서 최적 선택을 할 수 있다.

해답 및 풀이

import sys
input = sys.stdin.readline

N = int(input())
costs = []

for i in range(N):
    cost_R, cost_G, cost_B = map(int,input().split())
    costs.append([cost_R,cost_G,cost_B])

# 이웃집과 색이 같으면 안된다.
# dp[i][c] = 1번 집부터 i번 집까지 칠했을 때, i번 집을 색 c로 칠하는 경우의 최소 비용
dp = []
for _ in range(N):
    dp.append([0,0,0])

dp[0][0] = costs[0][0]
dp[0][1] = costs[0][1]
dp[0][2] = costs[0][2]

for i in range(1,N):
    dp[i][0] = costs[i][0] + min(dp[i-1][1], dp[i-1][2])
    dp[i][1] = costs[i][1] + min(dp[i-1][0], dp[i-1][2])
    dp[i][2] = costs[i][2] + min(dp[i-1][0], dp[i-1][1])

    print(min(dp[N-1]))