백준 11659번: 구간 합 구하기 4 python

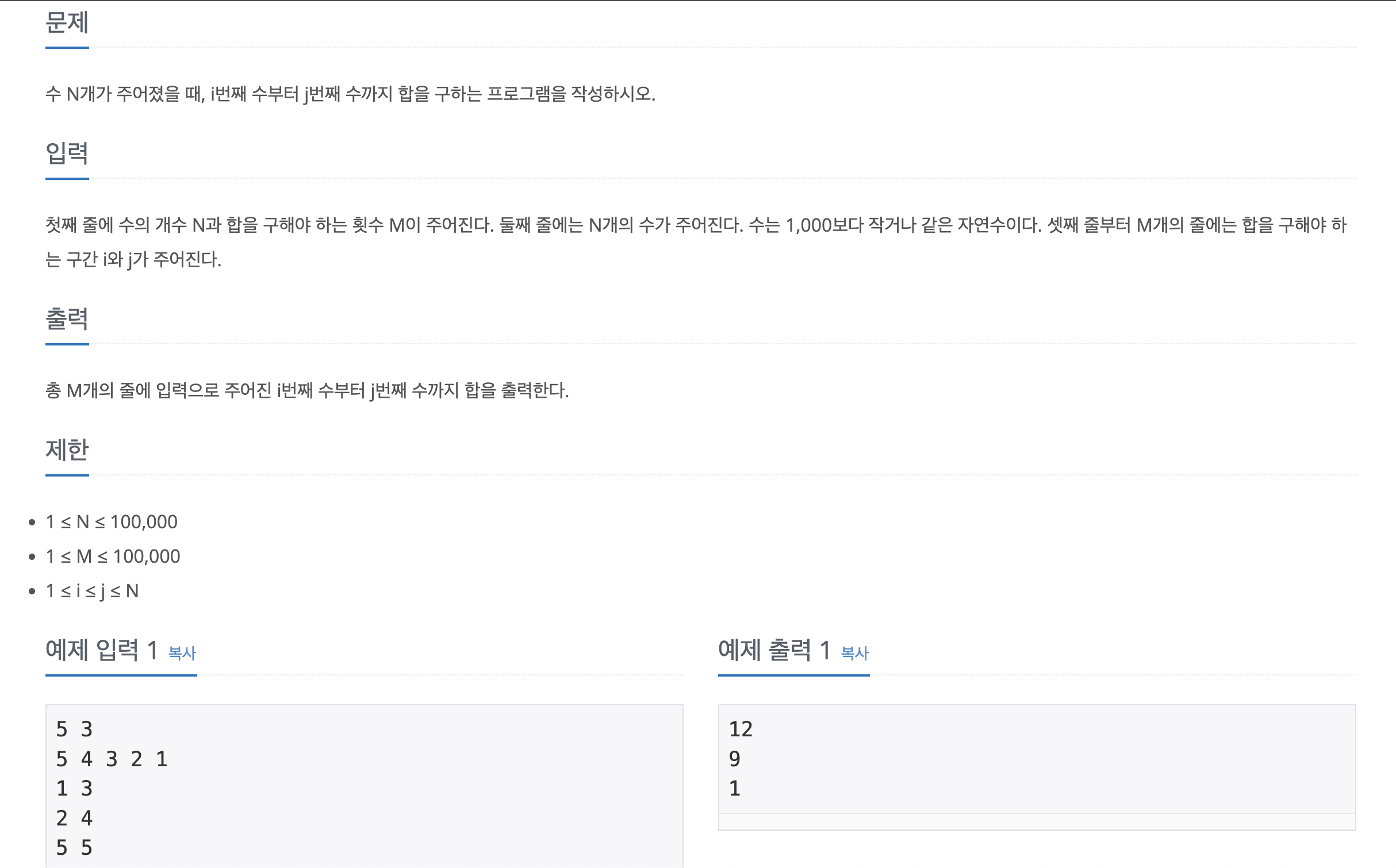
https://www.acmicpc.net/problem/11659

문제 접근

N과 M이 100,000 이하이고 시간도 1초로 제한되어 있다.
그냥 풀면 100% 시간 초과가 날 것 같다. 전처리가 필요하다.

이 경우 누적합을 미리 정의해놓고, 꺼내 쓰면 된다.

arr = [5, 4, 3, 2, 1] 에서 누적합을 구해보자.
S = [0, 5, 9, 12, 14, 15]로 누적합 리스트인 S를 구할 수 있다. (맨 처음 원소는 0으로 고정)
(Ex1) 0~2(인덱스)범위의 구간 합을 구해보자.
--> arr[0] + arr[1] + arr[2] = 5 + 4 + 3 = 12이다. 이렇게 하나씩 더할 필요없이 S[3] - S[0] = 12 - 0의 값을 계산해주어 0~2범위의 구간 합을 구할 수 있다.
(Ex2) 1~3범위의 구간 합을 구해보자.
--> arr[1] + arr[2] + arr[3]의 값을 구해주면 되는데, 위 예제처럼 리스트 S를 이용하여 풀면 S[4] - S[1] = 14 - 5 = 9로 해당 구간 합을 구할 수 있게된다.

-> 즉 i~j 범위 누적합은 S[j]-S[i-1]이다.

해답 및 풀이

import sys

N, M = map(int,sys.stdin.readline().split())
nums = list(map(int,sys.stdin.readline().split()))

sum_list = [0]
total = 0

for i in range(N):
    total += nums[i]
    sum_list.append(total) #sum_list에 누적합 저장


for _ in range(M):
    i, j = map(int, input().split())
    print(sum_list[j] - sum_list[i - 1]) #  i~j 범위 누적합은 S[j]-S[i-1]이다.
    
print(sum_list)

모르면 외우자
누적 합 !
i~j 범위 누적합은 S[j] - S[i-1] 이다.
( 단 S[0] = 0 처리를 해주어야 한다. )