백준 12865번: 평범한 배낭 python

https://www.acmicpc.net/problem/12865

문제 접근

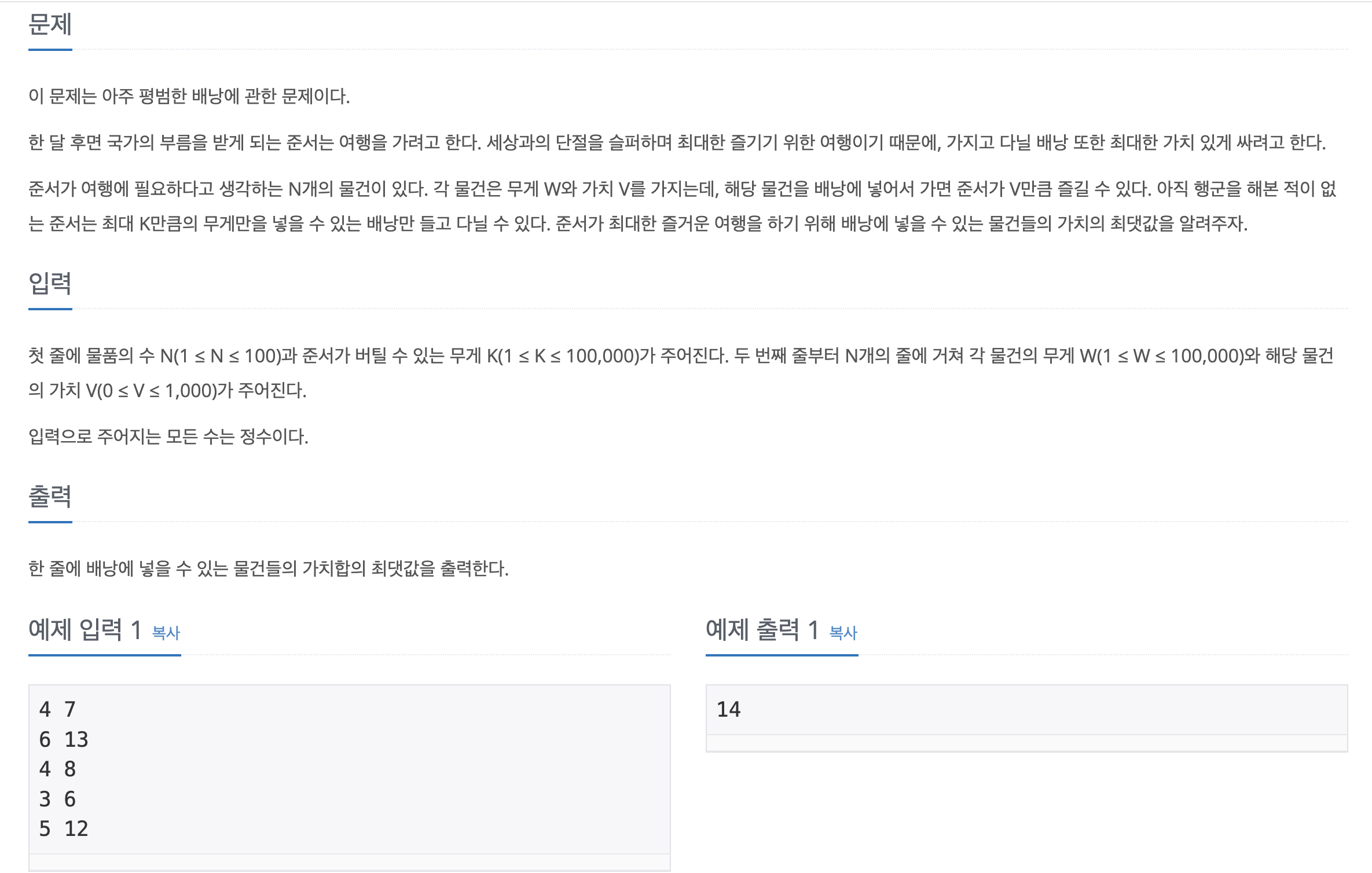
물건 N개, 무게 W, 가치 V, 최대 K만큼의 무게에 한해서 배낭에 넣을때 넣을 수 있는 물건들의 가치의 최댓값 출력하는 문제.

첫쨋줄에 N, K 를 입력받고 둘쨋줄 부터 W와 V를 입력받는다.

예제 입력 1에서
4 7 을 첫쨋줄에 입력받고 -> 물건 4개, 최대 7의 무게를 가질 수 있다는 의미

둘쨋쭐부터 무게 W, 가치 V 순으로 입력받음
6 13 -> 무게 6, 가치 13
4 8
3 6
5 12

일 경우 최대 가치의 값은 14이다.
=> 4 8 과 3 6을 택했을 때, 무게 7, 가치 14

dp 설계 :
dp[i][j] = i번째 물건까지 고려했을 때, 무게 j 나가는 것을 채웠을 때의 최대 가치

점화식 :

• i번째 물건을 넣지 않을 경우 :
  dp[i][j] = dp[i-1][j]
• i번째 물건을 넣을 수 있고 넣을 경우
  dp[i][j] = max(dp[i][j], dp[i-1]j-W[i] + V[i])

해답 및 풀이

import sys
input = sys.stdin.readline

# 입력 받기
N, K = map(int, input().split())  # N: 물건 수, K: 최대 배낭 무게
items = []

for _ in range(N):
    w, v = map(int, input().split())  # 각 물건의 무게 w, 가치 v
    items.append((w, v))

# DP 테이블 생성: (N+1) x (K+1) 이유는 아무것도 안넣을 때도 고려해야하므로, dp[0][j]는 항상 0, dp[i][0]도 무게 0이니 항상 0
dp = []
for _ in range(N + 1):
    row = [0] * (K + 1)
    dp.append(row)

# DP 채우기
for i in range(1, N + 1):  # i: 1번부터 N번 물건까지 고려
    weight, value = items[i - 1] # index 0 부터 고려해야하므로 i-1 처리
    for j in range(K + 1):  # j: 현재 배낭의 용량
        if j < weight:           
            dp[i][j] = dp[i - 1][j]
            #만약 현재 물건의 무게보다 배낭 용량이 작다면,
			#이 물건은 넣을 수 없으니
			#이전 결과 그대로 사용
        else:
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight] + value)
            # 현재 물건을 넣을 수 있다면:
            # 안 넣는 경우 vs 넣는 경우 중 큰 값을 선택

# 결과 출력
print(dp[N][K])