
난이도 : 골드 1
유형 : MST
출처 : https://www.acmicpc.net/problem/17472
문제 해석
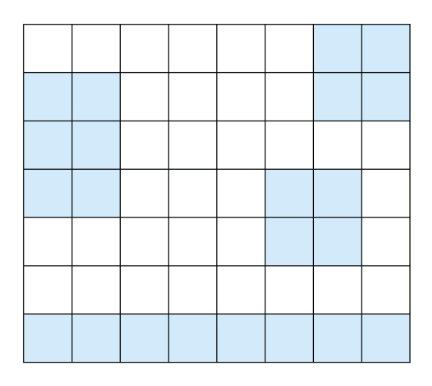
이렇게 어떤 나라의 지도가 있다. (N * M)
하늘색으로 색칠 된 곳이 땅, 아닌 곳이 바다라고 한다.
땅이 연결된 곳 한 덩이를 섬이라고 한다.
이 섬들에게 다리를 지어 모두 연결하려고 한단다.
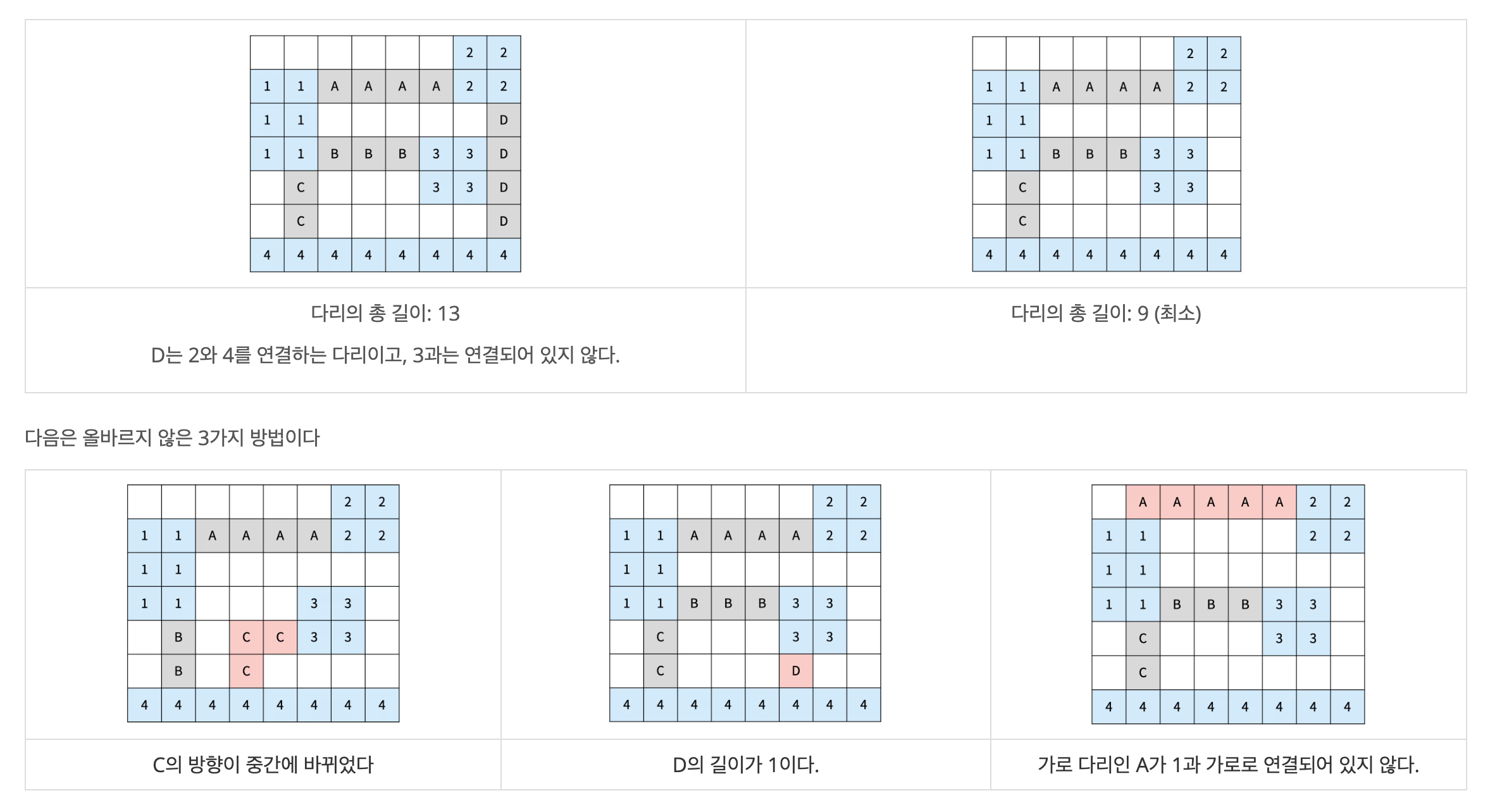
다리의 양 끝은 섬과 인접한 바다 위에 있어야 하고, 한 다리의 방향이 중간에 바뀌면 안된다. 또, 다리의 길이는 2 이상이어야 한다.
섬 A와 B를 연결하는 다리가 중간에 섬 C와 인접한 바다를 지나가는 경우에 섬 C는 A, B와 연결되어있는 것이 아니다.
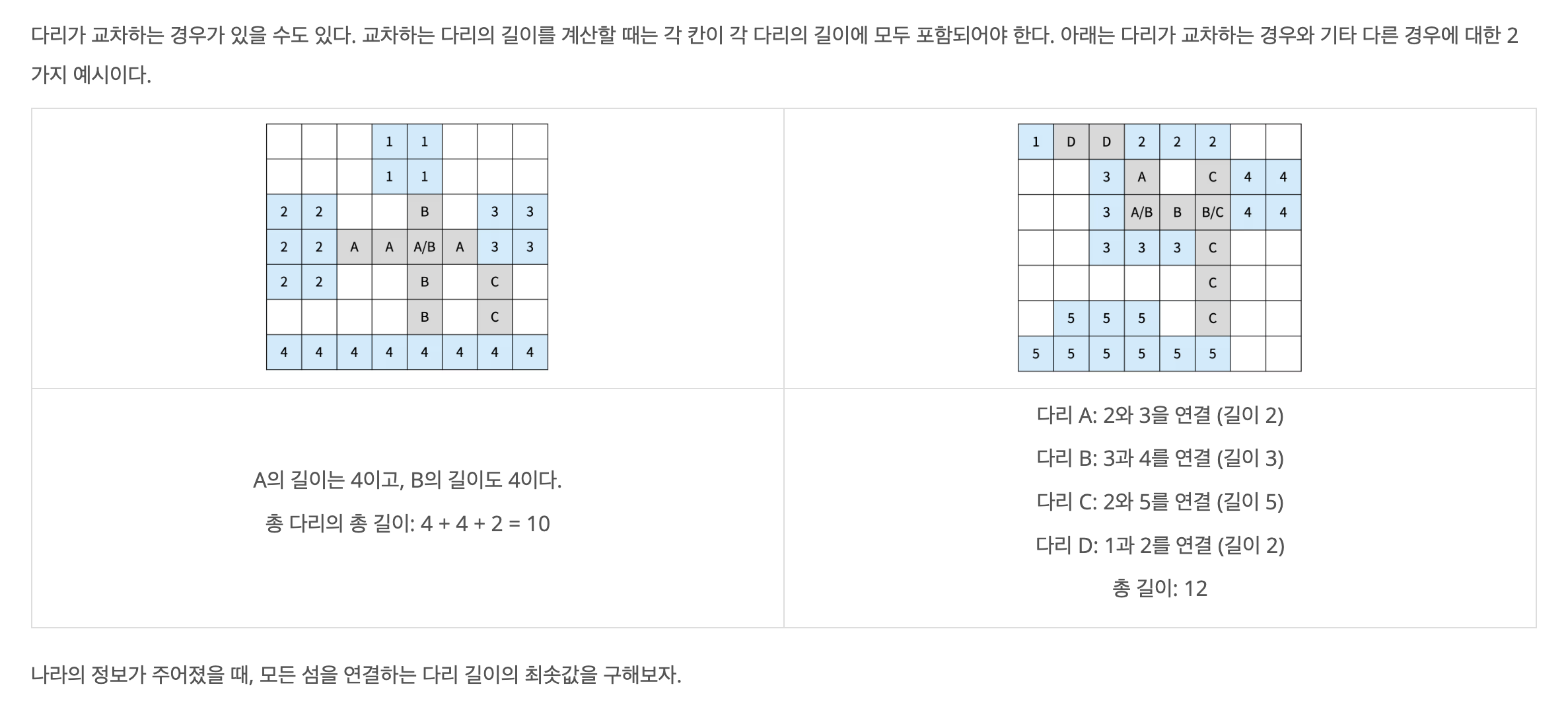
다리가 교차하는 경우가 있을 수도 있다. 교차하는 다리의 길이를 계산할 때는 각 칸이 각 다리의 길이에 모두 포함되어야 한다.
문제의 목표 : 지도 N*M 이 주어졌을 때 모든 섬을 연결하는 다리 길이의 최솟값을 출력.
모든 섬을 연결하는 것이 불가능하면 -1을 출력한다.
예제 1 을 보자
7 8
0 0 0 0 0 0 1 1
1 1 0 0 0 0 1 1
1 1 0 0 0 0 0 0
1 1 0 0 0 1 1 0
0 0 0 0 0 1 1 0
0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1이는 그림으로 표현하면 이렇게 생겼다.
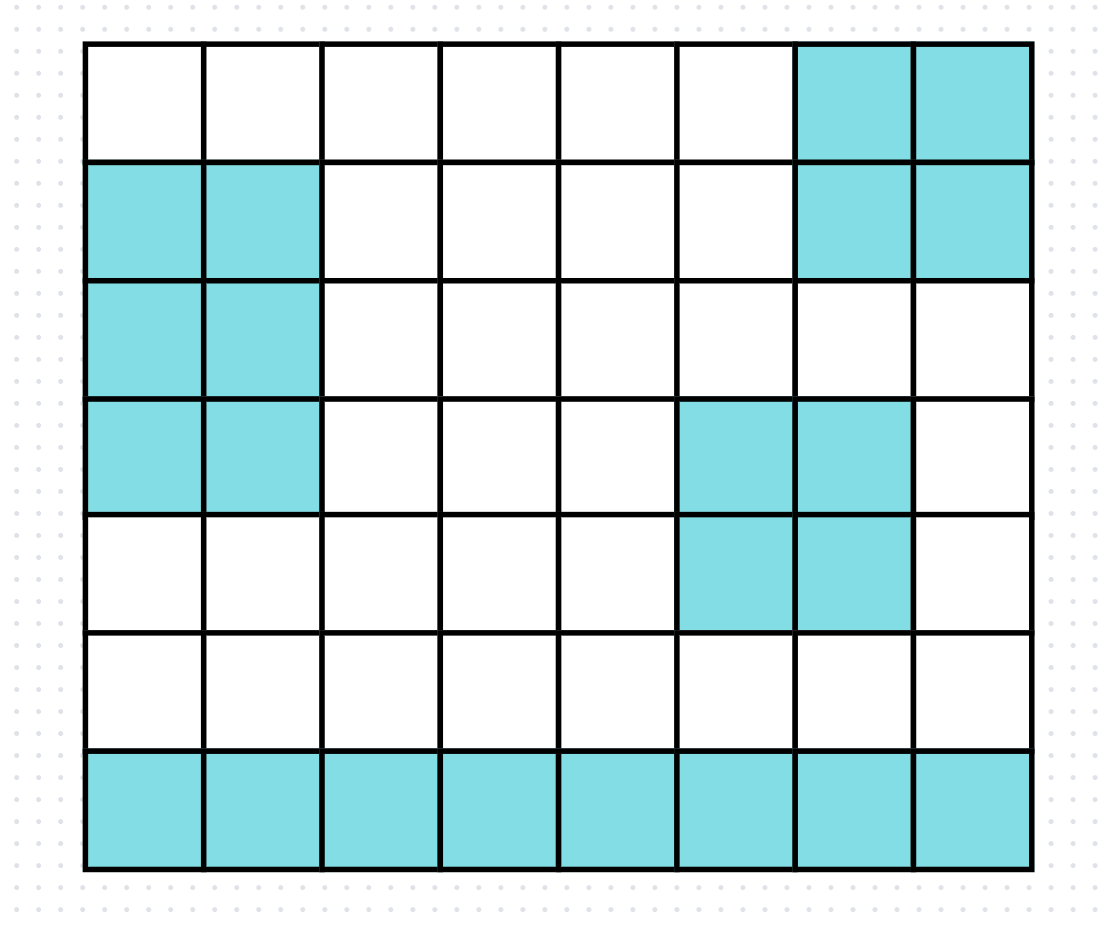
어떻게 하면 최소비용으로 다리를 놓을 수 있을까?
일단 가장 다리를 저렴하게 놓을 수 있는 비용은 2이다. 왜냐하면 다리 길이가 2 이상이라고 문제에서 주었다.
그렇기에 9시 방향 섬과 6시 방향 섬은 비용 2로 무조건 이어주어야 할 것 같고, 가운데쪽 네칸 짜리 섬은 비용 2로 지을 수 있는 다리가 없기에 그다음 비용인 3으로 9시방향 섬과 이어주어야 할 것 같다.
마지막 1시방향 섬은 3으로도 지을 수 없는 다리가 없기에 비용 4로 9시방향 섬과 이어주면, 총 비용 2 + 3 + 4 = 9로 모든 다리를 연결할 수 있게 된다.
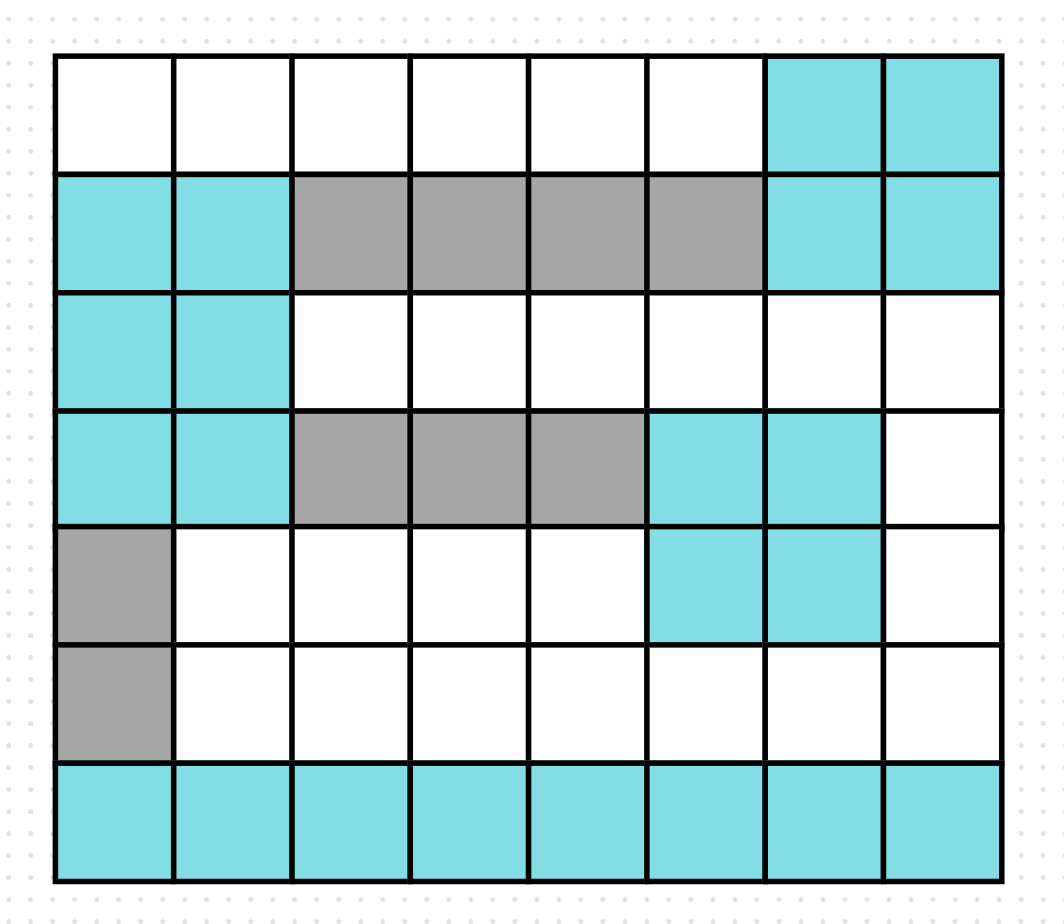
그렇다면 어떻게 이를 코드로 구현할까?
한 섬에서 다른 섬까지의 거리가 담겨져있는 배열이 필요할 것 같다.
그렇게 그 거리가 작은 순서대로 union() 해주면 mst_weight 를 구할 수 있을 것 같은데 어떻게 섬 간의 거리를 구할까?
전체 풀이 전략(Flow)
라벨링(섬 ID 붙이기)
격자에서 1로 연결된 덩이를 BFS/DFS로 묶어 섬 ID(1,2,…)를 붙인다.
이렇게 칸 단위 데이터를 섬 단위 그래프의 정점으로 압축한다.
경계 추출 → 레이캐스팅(다리 후보 수집)
각 섬의 경계 칸(사방 중 하나가 바다인 땅 칸)에서만 출발해 상/하/좌/우로 직선으로 쭉 전진.
처음 만난 다른 섬까지의 바다 칸 수가 ≥ 2이면 다리 후보(간선)로 저장.
같은 두 섬 사이에서는 최소 길이만 유지.
크루스칼(MST)
모든 다리 후보를 길이 오름차순으로 정렬 → Union-Find로 사이클 없이 선택.
선택된 간선 수가 섬 개수-1이 되면 총 길이 출력, 아니면 -1.
해답 및 풀이
import sys # 빠른 입력을 위해 sys 모듈 사용
from collections import deque # BFS/큐 구현을 위해 deque 사용
imput = sys.stdin.readline # (오타) input 단축 바인딩 의도 같음. 변수명이 'imput'라 실제로 쓰이지 않음
n, m = map(int, input().split()) # 격자 크기 입력: n행, m열
graph = [list(map(int, input().split())) for _ in range(n)] # n줄에 걸쳐 0/1 격자 입력 (0: 바다, 1: 땅)
visited = [[False] * m for _ in range(n)] # 라벨링 BFS용 방문 배열
dir = ((0, 1), (0, -1), (1, 0), (-1, 0)) # 4방향 (우,좌,하,상) — 변수명이 내장함수 dir와 겹침
edge = set() # (비용, 섬A, 섬B) 형태의 간선 후보들을 중복 없이 저장
def condition(ni, nj):
return ni < 0 or ni >= n or nj < 0 or nj >= m # 인덱스가 격자 밖인지 여부 반환(True면 범위 밖)
def marking(y, x, mark):
q = deque() # BFS 큐
q.append((y, x)) # 시작 좌표 추가
graph[y][x] = mark # 현재 땅을 섬 ID(mark)로 치환
visited[y][x] = True # 방문 처리
while q: # 연결된 땅(컴포넌트) 전체 라벨링
i, j = q.popleft()
for dy, dx in dir: # 4방향 이웃 확인
ni, nj = i + dy, j + dx
if condition(ni, nj) or not graph[ni][nj] or visited[ni][nj]:
continue # 범위 밖이거나 바다(0)이거나 이미 방문이면 스킵
graph[ni][nj] = mark # 같은 섬으로 라벨 지정
visited[ni][nj] = True # 방문 처리
q.append((ni, nj)) # 큐에 넣어 계속 확장
def getDist(y, x, now):
q = deque()
for idx in range(4):
q.append((y, x, 0, dir[idx])) # 한 출발점에서 4방향 '직선'으로 레이캐스팅 시작
while q:
i, j, cnt, nowDir = q.popleft() # cnt는 출발점에서 현재 칸까지 이동한 칸 수(바다 포함)
if graph[i][j] != 0 and graph[i][j] != now: # 현재 칸이 바다(0)가 아니고, 다른 섬을 만난 경우
if cnt > 2: # 다리 길이가 2 이상인지 확인(도착칸 포함이라 >2)
edge.add((cnt - 1, now, graph[i][j])) # 길이 = cnt-1 로 저장 (바다 칸 수), (중복 제거용 set)
continue # 이 방향 탐색은 종료
ni, nj = i + nowDir[0], j + nowDir[1] # 같은 방향으로 한 칸 더 전진
if condition(ni, nj) or graph[ni][nj] == now:
continue # 범위 밖이거나 자기 섬을 다시 만나면 이 방향 중단
q.append((ni, nj, cnt + 1, nowDir)) # 전진한 상태를 큐에 추가
mark = 1 # 섬 라벨 시작값(1부터)
for i in range(n):
for j in range(m):
if graph[i][j] and not visited[i][j]: # 아직 라벨링 안 된 땅(1)을 발견하면
marking(i, j, mark) # BFS로 해당 컴포넌트를 섬 ID=mark로 칠함
mark += 1 # 다음 섬을 위해 mark 증가
for i in range(n):
for j in range(m):
if graph[i][j] != 0: # 모든 땅 칸(=라벨된 섬 칸)에서
visited = [[False] * m for _ in range(n)] # (의미 없음) visited 초기화 — getDist에서는 사용 안 함
getDist(i, j, graph[i][j]) # 해당 칸을 출발점으로 4방향 직선 다리 후보 수집
edge = list(edge) # set → list 변환
edge.sort() # 비용(길이) 오름차순 정렬: (cost, a, b)
def findParent(parent, x):
if x != parent[x]: # 경로 압축: 루트를 향해 부모 갱신
parent[x] = findParent(parent, parent[x])
return parent[x] # 대표(루트) 반환
def unionParent(parent, a, b):
a = findParent(parent, a) # a의 루트
b = findParent(parent, b) # b의 루트
if a > b: # (단순) 루트 번호 비교로 병합(랭크 없이)
parent[b] = parent[a] # b 트리를 a 밑으로
else:
parent[a] = parent[b] # a 트리를 b 밑으로
parent = [i for i in range(mark)] # 섬 수만큼 부모 배열 준비(0..mark-1)
result = 0 # 선택된 간선(다리)들의 총 길이
num = 0 # 선택된 간선 개수
for cost, a, b in edge: # 짧은 다리부터 크루스칼 진행
if findParent(parent, a) != findParent(parent, b): # 서로 다른 컴포넌트면
num += 1 # 간선 수 +1
unionParent(parent, a, b) # 두 컴포넌트 합치기
result += cost # 총 비용 누적
if result == 0 or num != mark - 2: # MST 성립 체크: 간선 수가 (섬수-1)인지 확인
print(-1) # (참고) mark는 마지막에 +1 돼 있으니 (mark-2)가 K-1
else:
print(result) # 모든 섬 연결 성공 → 최소 총 길이 출력결국에 크루스칼 알고리즘을 적용하기 위해 섬들을 라벨링하고, 4방향을 BFS로 탐색하며 섬간의 거리를 구하는 과정을 떠올리고 구현하는 것이 굉장히 까다로웠다.
나중에 다시 이걸 본다면 getDist 함수 로직과 레이캐스팅이란 무엇인가에 대해 다시 공부해보면 도움이 될 것 같다.
