백준 1766번: 문제집 [python]

난이도 : 골드 2
유형 : 위상정렬, 우선순위 큐
https://www.acmicpc.net/problem/1766

문제접근

이 문제는 위상정렬 문제이므로 위상정렬에 대해 다시 떠올려본다.

위상정렬 알고리즘은 방향이 있고 cycle이 없는 DAG그래프에 대해 성립하고
진입차수가 0인 노드를 큐에 넣고 해당 노드의 간선들을 모두 제거하고 다시 진입차수가 0이된 노드들을 큐에 넣고 해당노드는 결과배열에 넣는 것을 반복하는 로직으로 구현되었었다.

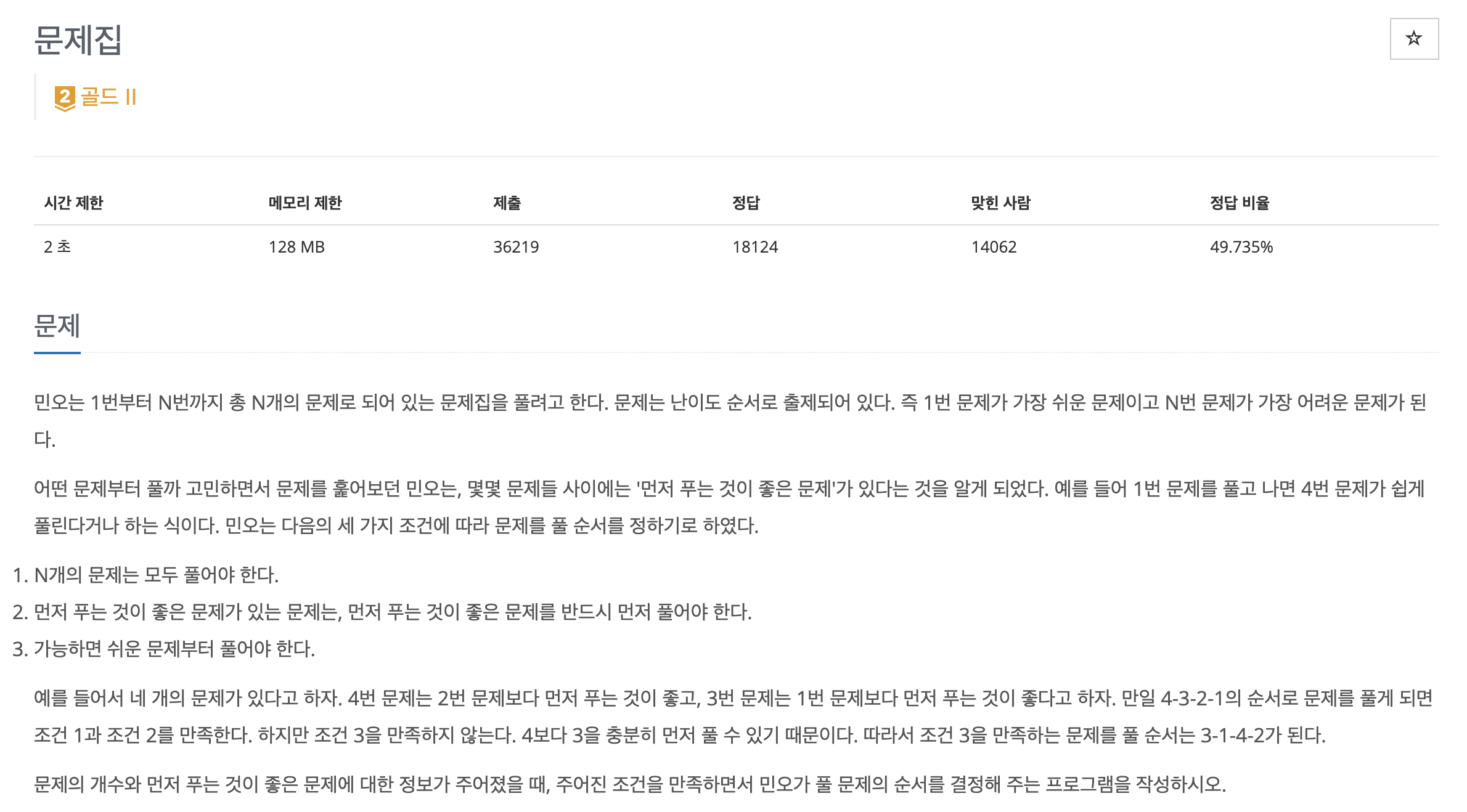
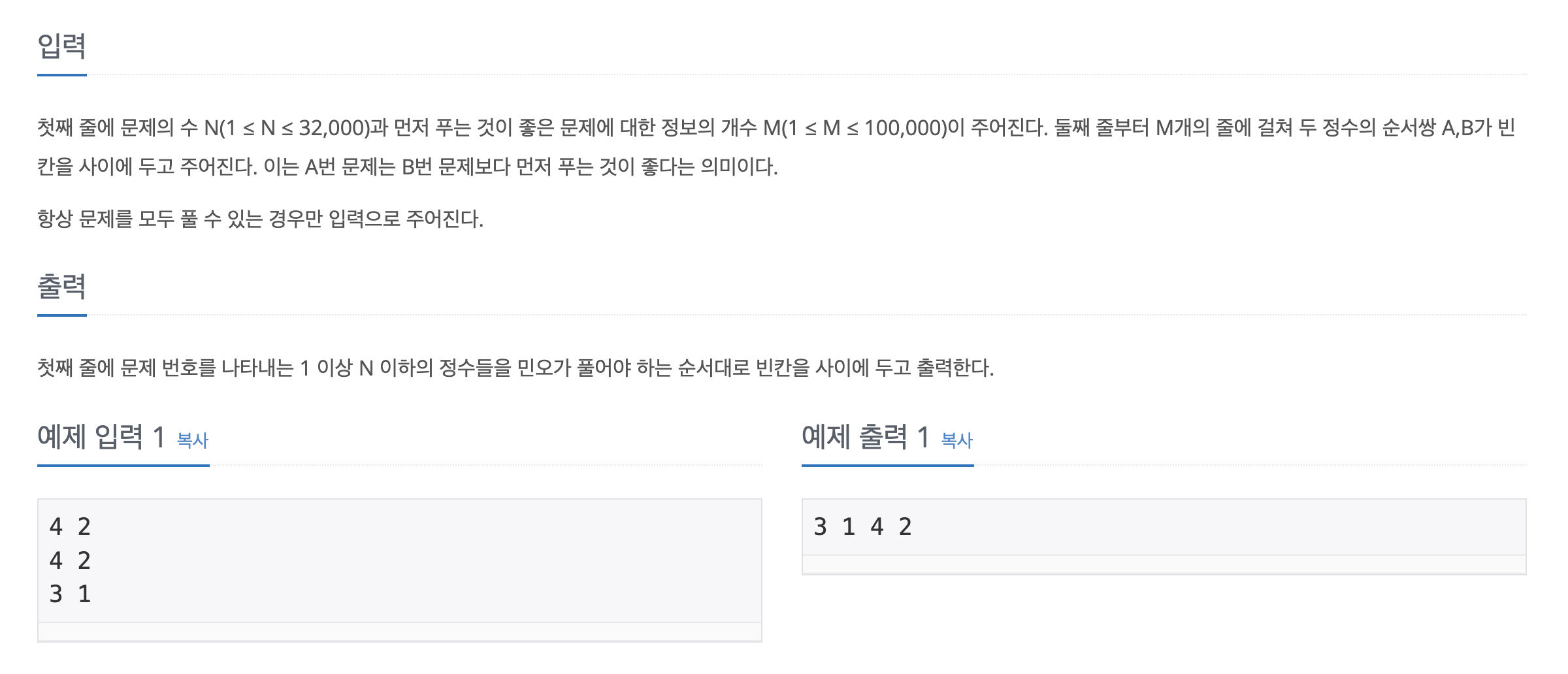
총 N개의 문제 (1번부터 N번)
M개의 정보가 주어짐.
A B → 문제 A를 먼저 풀어야 문제 B를 풀 수 있음
가능한 쉬운 문제부터 풀어야 함. 즉, 번호가 작은 문제부터 먼저 풀어야 함.

위상 정렬을 하되, 진입차수가 0인 노드가 여러 개일 경우 번호가 작은 것부터 먼저 선택해야 한다.
즉, 우선순위 큐(min-heap)을 사용해서 항상 가장 번호가 작은 문제부터 꺼내도록 구현하면 된다

#1. N, M 입력받기, 그래프 선언, 진입차수 배열 생성
#2. 간선 정보 입력받기
#3. 진입 차수가 0 인 노드들을 min-heap에 추가
#4. 힙 큐에서 빼내며 결과 리스트에 추가.
#4-1. 힙 큐에서 빼낸 노드에 간선을 삭제, 차수가 0이 된 노드가 있다면 heapq에 추가 ,반복

순으로 풀겠다.

해답 및 풀이

import heapq
import sys
input = sys.stdin.readline

#1. N, M  입력받기, 그래프 선언, 진입차수 배열 생성
N, M = map(int,input().split())

graph = []
for _ in range (N+1):
    row = []
    graph.append(row)

inDegree = [0] * (N + 1)

#2. 간선 정보 입력받기
for _ in range(M):
    a, b = map(int,input().split())
    graph[a].append(b)
    inDegree[b] += 1 

print(graph)
print(inDegree)

#3. 진입 차수가 0 인 노드들을 min-heap에 추가
heap = []

for i in range(N+1):
    if inDegree[i] == 0:
        heapq.heappush(heap, i)

#4. 힙 큐에서 빼내며 결과 리스트에 추가.
result = []

while heap:
    now = heapq.heappop(heap)
    result.append(now)
#4-1. 힙 큐에서 빼낸 노드에 간선을 삭제, 차수가 0이 된 노드가 있다면 heapq에 추가 ,반복
    for next in graph[now]:
        inDegree[next] -= 1

        if inDegree[next] == 0:
            heapq.heappush(heap, next)

print(*result)