백준 1929번 소수 구하기 python

https://www.acmicpc.net/problem/1929

해당 문제는 에라토스테네스의 체 문제이다.

에라토스테네스의 체

Sieve of Eratosthenes

고대 그리스의 수학자 에라토스테네스가 만들어 낸 소수를 찾는 방법. 이 방법은 마치 체로 치듯이 수를 걸러낸다고 하여 '에라토스테네스의 체'라고 부른다.

임의의 자연수 n에 대해 그 이하의 소수를 찾는 가장 간단하고 빠른 방법이다.

에라토스테네스의 체는 '특정 범위 내의 소수' 를 판정하는 데에만 효율적.

예를 들어 144까지의 숫자 중 소수를 찾는다고 하자.

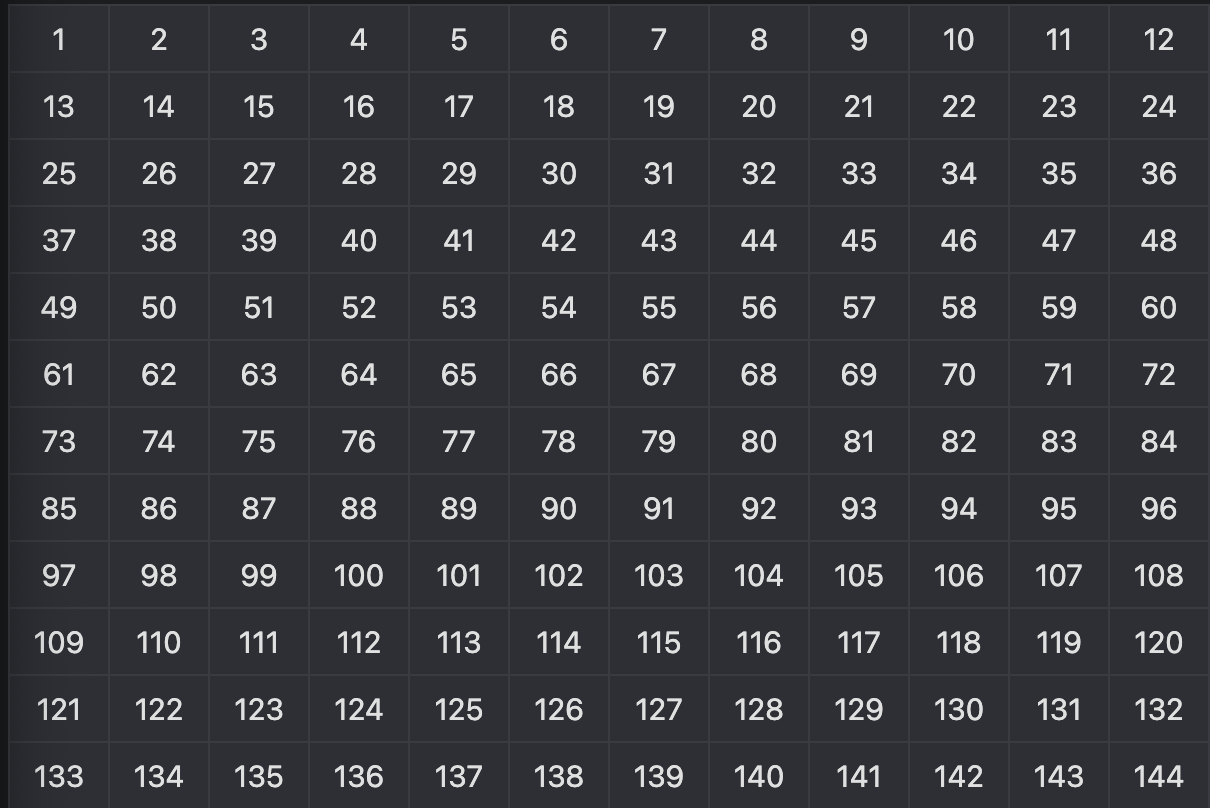
1. 소수도, 합성수도 아닌 유일한 자연수 1 제거
2. 2를 제외한 2의 배수를 제거.
3. 3을 제외한 3의 배수를 제거.
4. 4의 배수는 (2) 때 이미 지워졌으니 5의 배수 제거
5. 6도 (2)때 이미 지워졌으니 7의 배수 제거
   6, 같은이유로 나아가 11의 배수 제거

tip : 1~n의 소수를 알고 싶다면 루트 n이하의 수의 배수만 지우면 됨.

소스코드

m,n = map(int,input().split())

for i in range(m,n+1):
	if i == 1:
    	continue
    for j in range(2, int(i**0.5)+1):
    	if i % j == 0:
        break
    else:
    	print(i)

예시로 2,10 이 입력되었을 때를 보자.

1. i=2

int(2**0.5) = 1.414 인데 int를 씌우면 소수점을 버리는 내림연산을 함. 고로 1이 됨
range(2,1+1) = range(2,2) 인데 이는 2이상 2미만 이므로 빈 시퀀스라 내부 반복문이 실행되지 않으므로 else 블록이 실행됨

print(2)

2. i=3

마찬가지로 range(2,2) 가 나와
print(3)

3. i=4

int(4**0.5) = 2
range(2,2+1) = range(2,3) 이 되며
j 값이 2가 됨

내부 루프가 실행되고
j=2:
4%2 == 0이므로 조건이 만족하므로 break가 바로 발생하여 포문이 즉시 종료됨.
else 블록이 실행되지 않았으므로 출력이 없음.

이런식으로 쭉쭉 가서

i = 10 일 때를 보면

int(10**0.5) = 3.162... 이므로 = 3
range(2,4) 가 되므로 j는 2,3이 나온다.

j = 2 일때,
10 % 2 == 0 이므로 바로 break

이런식으로 포문이 돌아가며 총 출력은
2
3
5
7
이 나오며 2와 10사이에 소수들이 출력된다.