백준 2630번: 색종이 만들기 [python]

tomkitcount·2025년 6월 10일

백준 알고리즘

알고리즘

목록 보기

74/304

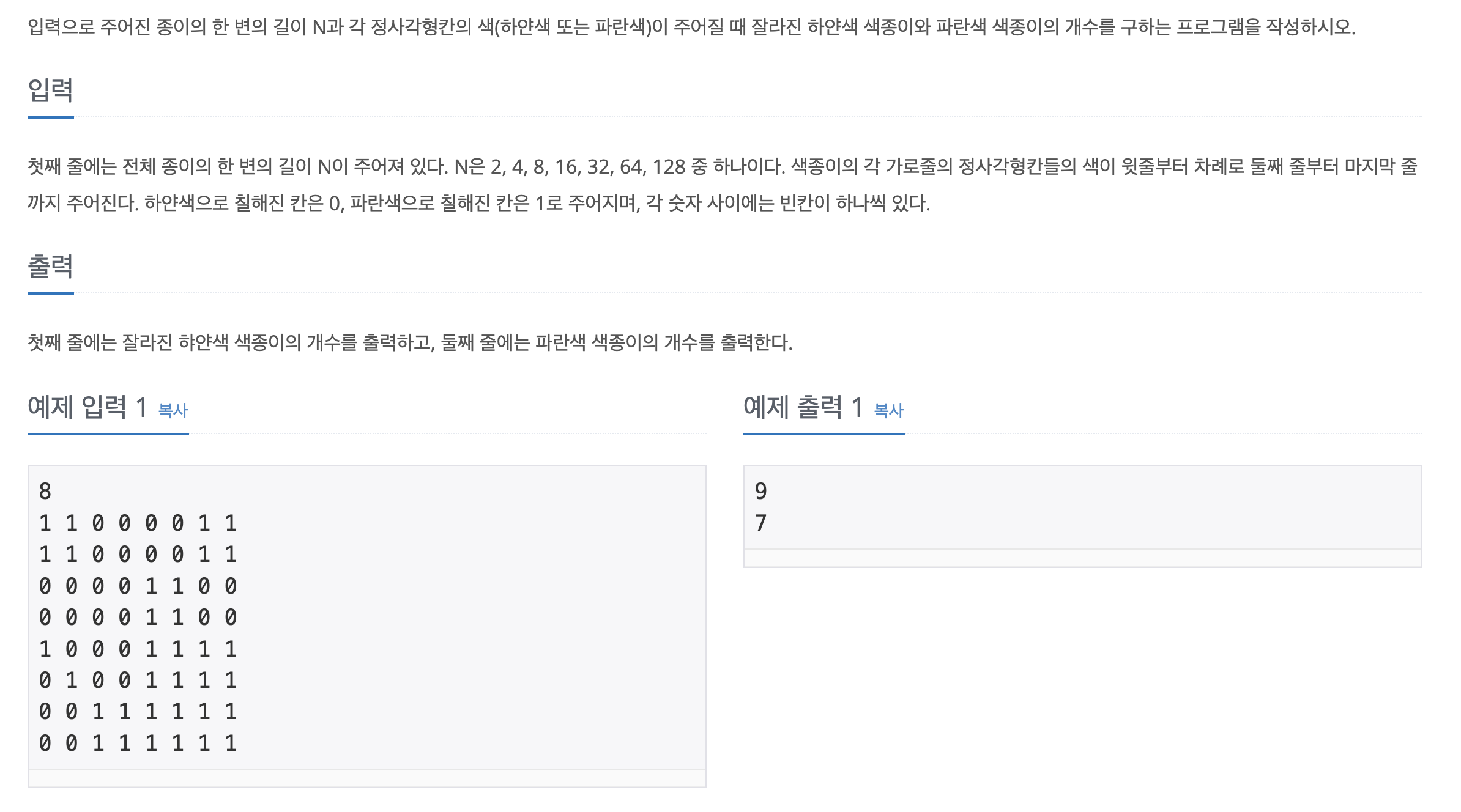
https://www.acmicpc.net/problem/2630

백준 분할정복 첫문제

분할정복이란?

큰 문제를 작은 문제로 나눠서(분할), 각 문제를 재귀적으로 해결한 다음, 그 결과를 합쳐서 전체 문제를 해결하는 알고리즘 전략.

분할 정복의 3단계 구조

Divide (분할)

→ 문제를 더 작은 하위 문제들로 나눈다.
→ 일반적으로 문제의 입력 크기를 절반으로 나누는 식이 많음.

Conquer (정복)

→ 하위 문제를 재귀적으로 해결한다.
→ 하위 문제 크기가 충분히 작아지면 재귀 호출을 멈추고 직접 해결 (기저 조건)

Combine (결합)

→ 하위 문제의 해를 조합하여 원래 문제의 해를 만든다.

문제로 돌아와서.

문제 접근

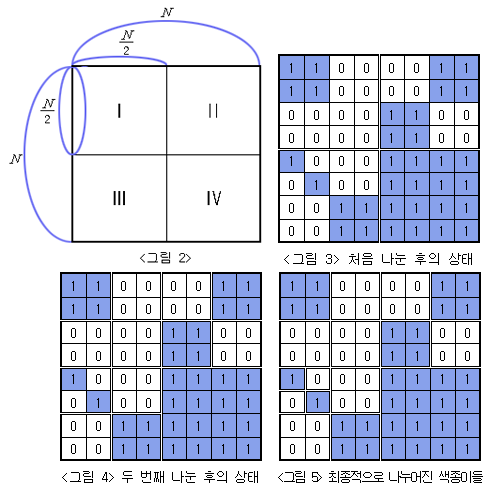
전체 종이가 모두 같은 색으로 되어있지 않으면 → 4등분해서 각각 재귀 처리하기

import sys
input = sys.stdin.readline

N = int(input()) 
lst = []
for _ in range(N):
  lst.append(list(map(int, input().split()))) # N*N 크기 2차원 배열, 색종이 정보 저장

def conquer(n, lst): # n 은 lst의 한 변의 길이, 즉 이중 리스트의 크기
  # lst 안에 1이 하나도 없는 경우 = 다 0 인 경우
  if not any(1 in i for i in lst):
    lst_cnt.append(0)
    return # 0을 결과 리스트에 추가하고 재귀 종료
  # lst 안에 0이 하나도 없는 경우 = 다 1 인 경우
  elif not any(0 in i for i in lst):
    lst_cnt.append(1)
    return # 1을 결과 리스트에 추가하고 재귀 종료
  else: # 0 , 1 섞인 경우, 색이 섞여 있으므로 4등분 필요
    lst_0 = []
    lst_1 = []
    for i in lst:
      lst_0.append(i[:n//2]) # 각 행의 왼쪽 절반 (열 기준)
      lst_1.append(i[n//2:]) # 각 행의 오른쪽 절반 (열 기준)
    conquer(n//2, lst_0[:n//2])  # 왼쪽 위
    conquer(n//2, lst_0[n//2:])  # 왼쪽 아래
    conquer(n//2, lst_1[n//2:])  # 오른쪽 아래
    conquer(n//2, lst_1[:n//2]) # 오른쪽 위
    return


lst_cnt = []
conquer(N, lst)
print(lst_cnt.count(0))
print(lst_cnt.count(1)) # 최종적으로 하얀색(0)과 파란색(1) 색종이의 개수를 각각 출력

any 문법

if not any(1 in i for i in lst):
lst는 2차원 리스트 (즉, 리스트 안에 리스트들)

1 in i for i in lst 는 각 i가 행(row)일 때, 해당 행 안에 1이 있는지를 확인

이걸 any()로 감싸면, "하나라도 1이 있는 행이 있다면 True 반환"

슬라이싱 문법

i[:n//2]     # i의 앞쪽 절반
i[n//2:]     # i의 뒤쪽 절반

i = [1, 2, 3, 4]
n = 4

i[:2]   # [1, 2]
i[2:]   # [3, 4]

lst_0.append(i[:n//2])  # 각 행의 왼쪽 절반 (열 기준)
lst_1.append(i[n//2:])  # 각 행의 오른쪽 절반 (열 기준)


conquer(n//2, lst_0[:n//2])   # 왼쪽 위   (왼쪽 열 + 위쪽 행)
conquer(n//2, lst_0[n//2:])   # 왼쪽 아래 (왼쪽 열 + 아래쪽 행)
conquer(n//2, lst_1[n//2:])   # 오른쪽 아래 (오른쪽 열 + 아래쪽 행)
conquer(n//2, lst_1[:n//2])   # 오른쪽 위   (오른쪽 열 + 위쪽 행)

lst_0[:n//2] lst_0[n//2:] 가 어떻게 위아래로 나뉘는가?

예시: 4x4 종이

lst = [
  [1, 1, 0, 0],  # 0행
  [1, 1, 0, 0],  # 1행
  [0, 0, 1, 1],  # 2행
  [0, 0, 1, 1],  # 3행
]
n = 4

좌우 나누기

lst_0 = []
lst_1 = []
for i in lst:
    lst_0.append(i[:n//2])  # i[:2] → [0번째, 1번째 열] = 왼쪽 절반
    lst_1.append(i[n//2:])  # i[2:] → [2번째, 3번째 열] = 오른쪽 절반

#결과
lst_0 = [ [1, 1],
          [1, 1],
          [0, 0],
          [0, 0] ]  # 4x2 리스트, 왼쪽 절반

lst_1 = [ [0, 0],
          [0, 0],
          [1, 1],
          [1, 1] ]  # 4x2 리스트, 오른쪽 절반

위아래 나누기

lst_0[:n//2]     # = lst_0[:2]
lst_0[n//2:]     # = lst_0[2:]

#결과
lst_0[:2]  → [ [1, 1],     ← 위쪽
               [1, 1] ]

lst_0[2:]  → [ [0, 0],     ← 아래쪽
               [0, 0] ]