ER 모델

ER 모델 Entity Relationship Model은 개념적 모델링의 추상화 결과에 사용되는 대표적인 모델입니다.

ER 모델은 현실에 존재하는 개체들을 개체 Entity로 정의하고, 개체 간의 관계 Relationship를 표현함으로써 모델링합니다. 이때 각 개체들의 특성을 속성 Attribute으로 표현하여 개체를 식별합니다.

ER 모델은 ERD Entity Relationship Diagram이라는 다이어그램을 통해 시각화하여 표현합니다. 지난 포스트에서 개념적 모델링을 설명드리면서 보여드렸던 그림이 완벽하지는 않지만 ER 다이어그램이라고 생각하시면 됩니다.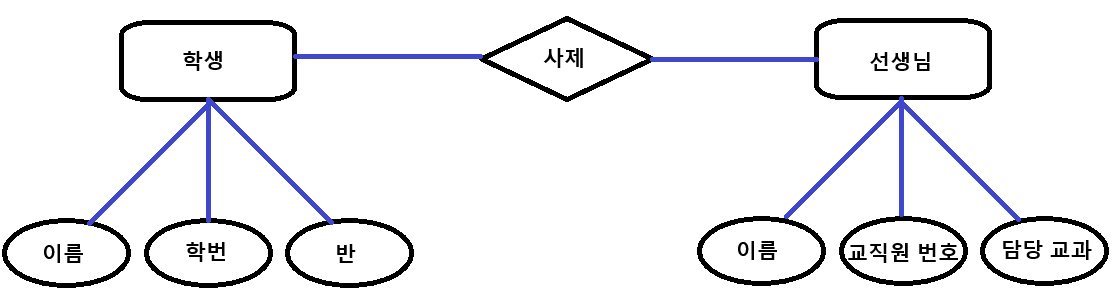

아래 ERD에서 설명할 예정이지만 마름모가 관계, 사각형이 개체, 타원이 속성으로 표기됩니다. 이들을 선으로 이어서 관계를 표현하는 것이 ERD 입니다.

그러면 우선 ER 모델을 구성하는 개체, 속성, 관계에 대해 알아보고 그 다음에 이들을 어떻게 ERD로 표현하는지 알아보도록 하겠습니다.

개체 Entity

개체 Entity는 사물, 동식물, 사람, 장소, 개념과 같이 현실 세계에서 독립적으로 존재하는 객체를 의미합니다. 데이터베이스에 저장하고자 하는 대상이 바로 개체입니다.

개체의 공통적인 속성 구조들을 추상화하여 분류한 것을 개체 타입, 특정 개체 타입에 속하는 실재 존재하고 있는 개체들의 집합을 개체 집합이라고 부릅니다.

강한 개체와 약한 개체

개체는 다시 강한 개체와 약한 개체로 나뉘어집니다.

강한 객체는 일반적으로 '개체'라고 표현할 때 가리키는 개체로 다른 개체의 참조 없이 독립적으로 존재할 수 있는 개체입니다. (관계가 없다가 아님!)

약한 객체는 독립적으로 존재하지 못하고 상위 개체 타입을 가져야하는 개체입니다.

학생의 학부모 개체가 존재한다고 하면 학부모 개체는 학생의 개체가 존재해야지만 존재할 수 있기 때문에 학생 개체는 강한 개체 학부모 개체는 약한 개체가 됩니다.

속성 Attribute

속성 Attribute는 개체가 가지고 있는 특성을 의미합니다. 예를 들어 학생이라는 개체는 [학번, 이름, 주소, 학과]와 같은 속성으로 정의할 수 있습니다.

속성은 다시 속성값의 형태에 따라 더 세분화된 속성 유형으로 구분합니다.

• 단순 속성, 복합 속성
  단순 속성은 더 이상 분해될 수 없는 속성을 의미하고 복합 속성은 더 세부적이고 독립적인 개념으로 분해할 수 있는 속성을 의미합니다.
  학과와 같은 속성의 경우 더 이상 분해될 수 없지만 주소의 경우에는 시군구, 동읍면 등으로 한 번 더 분해될 여지가 있는 복합 속성이라고 할 수 있습니다.

• 단일값 속성, 다중값 속성
  단일값 속성은 속성값으로 단 하나의 값만을 갖는 속성을 의미하고 다중값 속성은 여러 값을 가질 수 있는 속성을 의미합니다.
  학번의 경우 한 학생이 여러 학번을 부여받을 수 없고, 학과의 경우 복수 전공 등을 통해 여러 값을 가질 수 있기 때문에 다중값 속성이 될 수 있습니다.

• 저장 속성, 유도 속성
  저장 속성은 다른 속성에 영향을 받지 않고 독립적으로 저장되는 속성을 의미하고 유도 속성은 다른 저장 속성으로부터 유도(계산 등)된 속성을 의미합니다.
  입학년도와 졸업년도 속성이 존재한다면 입학년도는 독립적으로 입학한 년도에 저장되는 속성이고, 졸업년도는 입학년도로부터 4년 후의 날짜가 계산되어 저장되는 유도 속성이라고 할 수 있습니다.

관계 Relationship

관계 Relationship은 개체와 개체 사이의 연관성을 표현하는 것입니다. 선생님 개체와 학생 객체는 '가르친다-배운다'라는 관계 개념으로 연관됩니다.

이때 '가르친다-배운다'와 같은 정의될 수 있는 관계는 관계 타입이라고 부릅니다.

관계 타입의 유형

관계 타입은 각 개체가 관계를 맺은 차수(몇 개의 개체와 연관), 관계 대응수에 따라 더 세부적인 유형으로 나뉘어 집니다.

차수에 따른 유형

차수 Degree는 하나의 관계에 몇 개의 개체 타입이 관계되어 있는지를 의미합니다.

• 1진 관계
  1진 관계는 한 개체가 자기 자신과 관계를 맺는 관계입니다.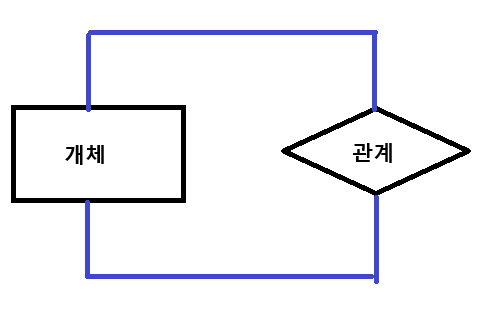예를들어 한 학급에서 모둠을 나눈다면 모둠장 학생은 모둠원 학생을 관리하게 됩니다. 이때 모둠장과 모둠원 모두 학생이라는 개체에서 선출되므로 학생 개체가 학생 개체와 관계를 맺는 1진 관계가 됩니다.

• 2진 관계
  2진 관계는 두 개체가 관계를 맺는 경우입니다.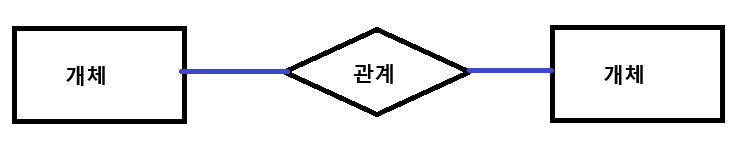계속 예시를 들었던 학생-선생 관계가 일반적인 2진 관계라고 할 수 있습니다.

• 3진 관계
  3진 관계는 세 개의 개체가 관계를 맺는 경우를 의미합니다.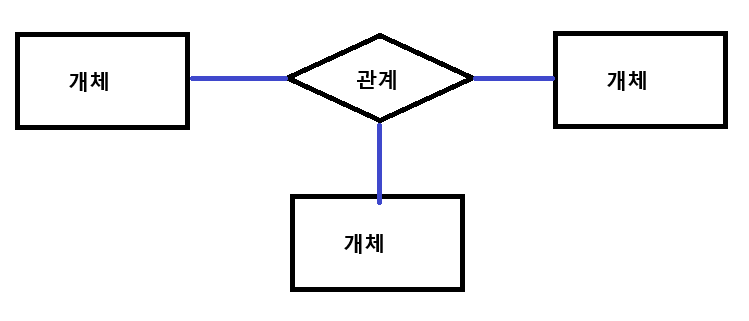

관계 대응수에 따른 유형

관계 대응수 Cardinality는 두 개체 타입 관계에 참여하게 되는 실제 개별 개체 수를 의미합니다.

• 1:1 관계
  좌측 개체와 우측 개체의 개별 개체가 1:1로 연관되는 관계를 1:1관계라고 합니다.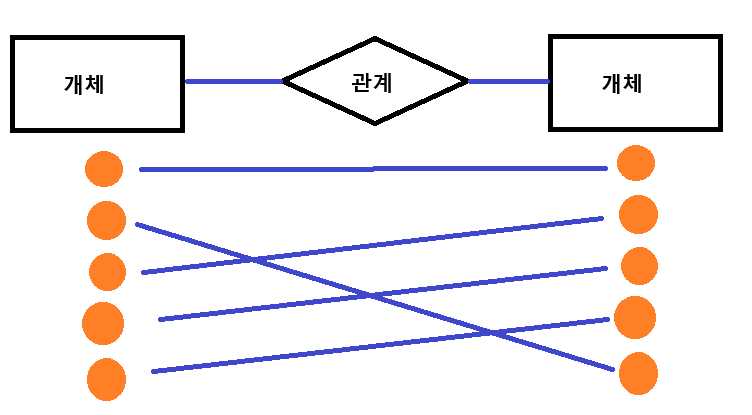

• 1:N or N:1 관계
  1:N or N:1 관계는 한 개체의 개별 개체가 다른 개체의 개별 개체 여러 개과 관계를 맺는 경우입니다. 현실에서 가장 많이 볼 수 있는 형태의 관계이기도 합니다.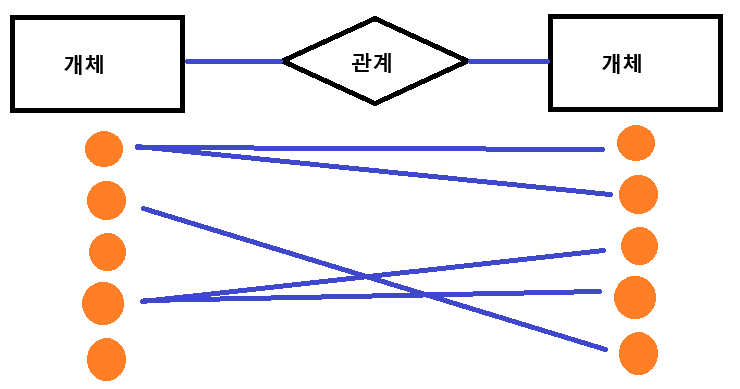

• M:N 관계
  M:N 관계 (다대다 관계)는 개별 객체들이 다른 개체와 복합적인 관계를 갖는 경우입니다.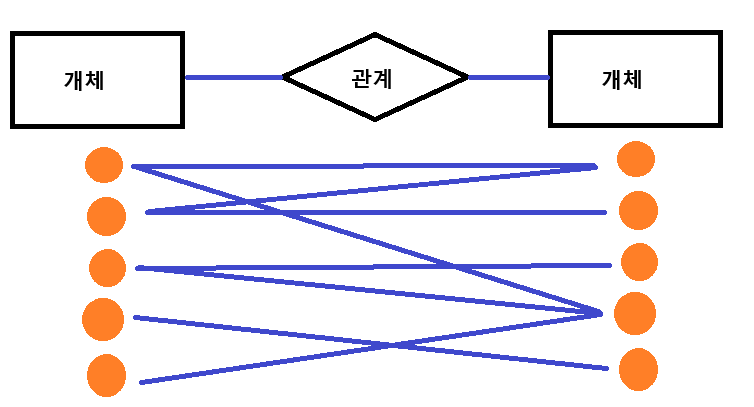

---

관계 대응수 최솟값, 최댓값

관계 대응수를 표현할 때 최솟값과 최댓값은 (최솟값, 최댓값)의 형태로 나타냅니다. 말 그대로 관계에 참여하는 개별 개체 수가 최솟값 만큼은 있어야하고, 최댓값만큼은 넘지말아야한다는 것을 의미합니다.

최솟값과 최댓값은 0 이상의 자연수를 가지고, 최댓값을 따로 지정하지 않는 경우 *을 사용해서 표기합니다. 만약 (0, *)이라고 표기하면 최솟값이 0이고 최댓값은 따로 지정하지 않는 임의의 값을 사용한다는 것을 표기하게 됩니다.

---

ERD 표기

이제 ER 모델에서 사용되는 개념들에 대해 알아보았으니 이들을 어떻게 다이어그램으로 표현하는 지에 대해서 알아보도록 하겠습니다.

개체 표기

• 개체
  개체(일반 or 강한 개체)는 다음과 같이 사각형으로 표기합니다.

• 약한 개체
  약한 개체는 사각형을 이중으로 표현합니다.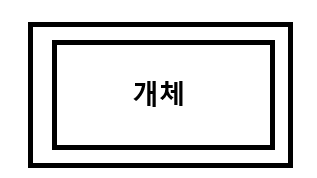

속성

• 속성
  일반 속성은 다음과 같이 타원으로 표기합니다.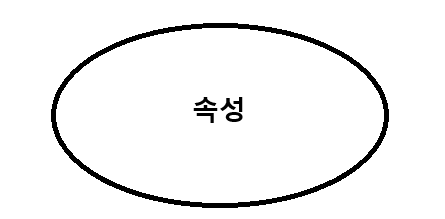

• 키 속성
  키 속성은 개체를 유일하게 식별 가능한 속성을 의미하며 속성 이름에 밑줄을 그어 표시합니다.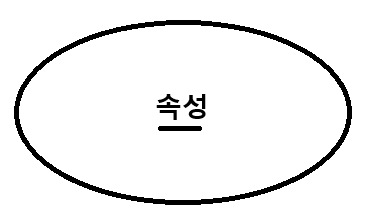

• 약한 개체 식별자
  약한 개체는 키 속성을 가질 수 없고 식별자만을 갖습니다. 즉, 약간 개체를 유일하게 식별 가능하게 하는 속성입니다.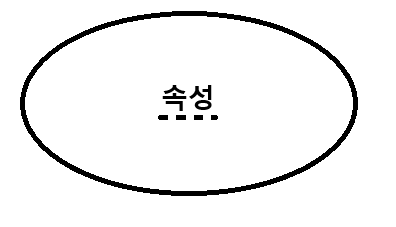

• 다중값 속성
  다중값 속성은 이중으로 표현합니다.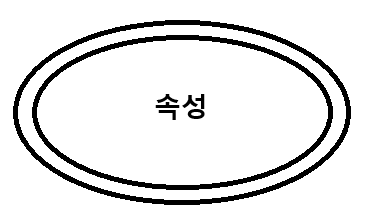

• 유도 속성
  유도 속성은 타원을 점선으로 표현합니다.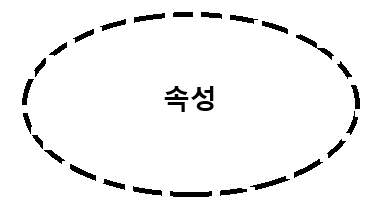

• 복합 속성
  복합 속성은 다음과 같이 큰 타원 아래 작은 타원 속성들을 명시해 표현합니다.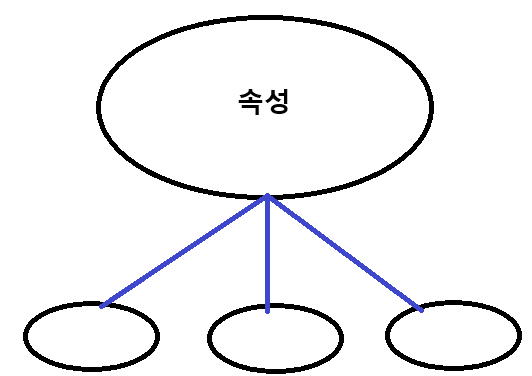

관계

관계는 마름모로 표현합니다.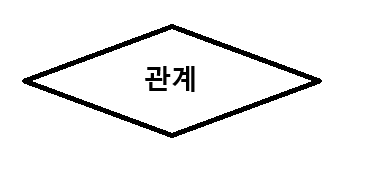

관계 대응수의 표기는 개체-관계 연결 실선 위에 표기합니다. 관계에 따라 1:1, 1:N. N:1, M:N을 표기합니다.

관계 대응수의 최솟값, 최댓값 표기는 관계 표기 아래쪽에 적습니다. 1: N 관계(혹은 N:1)에서 다수가 되는 쪽에 N을 적어주지만 최솟값, 최댓값의 표기는 1이 되는 개체의 실선 아래에 적어줍니다.

ISA 관계

공통 속성을 갖는 상위 개체와 공통 속성과 고유 속성을 갖는 하위 개체가 있다면 상하 관계를 갖는 ISA 관계라고 표현합니다. 이는 다음과 같이 역삼각형 모양으로 표현합니다.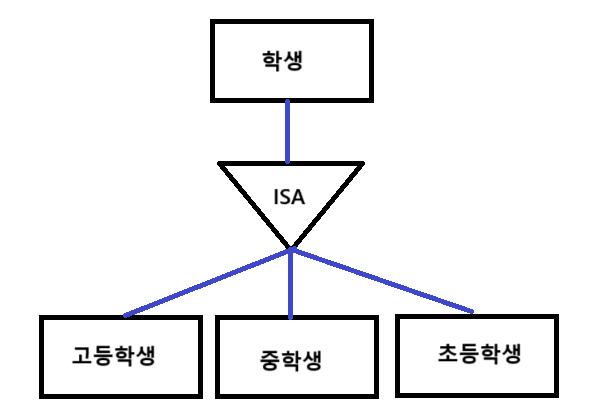

참여 제약 조건

참여 제약 조건은 개체 집합 내의 개별 개체들이 관계에 참여하는지 아닌지 여부에 따라 전체 참여, 부분 참여로 구분합니다.

전체 참여는 두 줄 실선, 부분 참여는 한 줄 실선으로 표현합니다.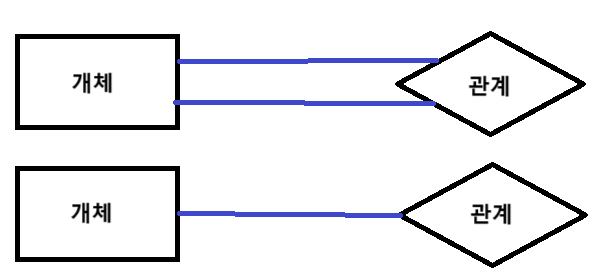

역할

일반적으로 관계를 통해서 개체의 역할을 파악할 수 있습니다. 그러나 만약 관계 이름만으로 개체의 역할이 명확하지 않다면 관계 실선에 역할을 명시해줍니다.