이번에 소개할 알고리즘은 그래프 탐색 그 중에서도 깊이 우선 탐색 DFS와 너비 우선 탐색 BFS입니다.
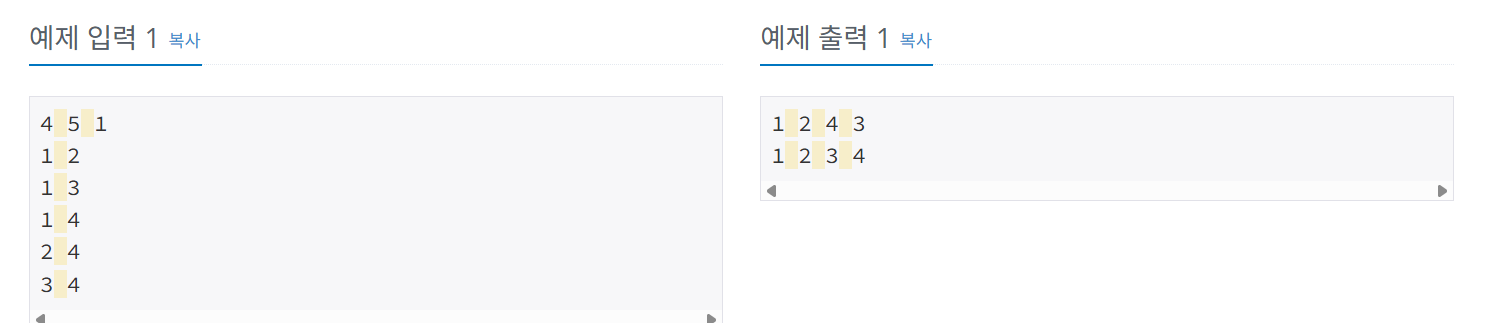
이번에는 알고리즘 문제 사이트인 백준에서 가져온 한 문제를 가지고 설명해볼까 합니다.
문제 - 1260번 DFS와 BFS
https://www.acmicpc.net/problem/1260
예전에 포스트로 작성한 적이 있긴한데요. 해당 포스트가 오래되었기도 하고 C로 작성되어있어서 Java로 재작성하는 동시에 설명을 최신화 하고자 다시 작성하게 되었습니다.
다음과 같은 선수 지식이 필요합니다.
구현 준비
아래 문단들에서 DFS, BFS 구현에 집중하기 위해 미리 다음과 같은 코드를 준비합니다.
public class Main {
private static int[][] graph;
public static void solution() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
graph = new int[n + 1][n + 1];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine(), " ");
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
graph[start][end] = 1;
graph[end][start] = 1;
}
sb.append(dfs(n, m, v)).append("\n");
sb.append(bfs(n, m, v)).append("\n");
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
public static String dfs(int n, int m, int v) {}
public static String bfs(int n, int m, int v) {}
public static void main(String[] args) throws IOException {
solution();
}
}private static int[][] graph: 간선 정보를 저장하는인접 행렬입니다..
문제에서 주어진 간선 정보를 토대로 그래프를 그리면 다음과 같습니다.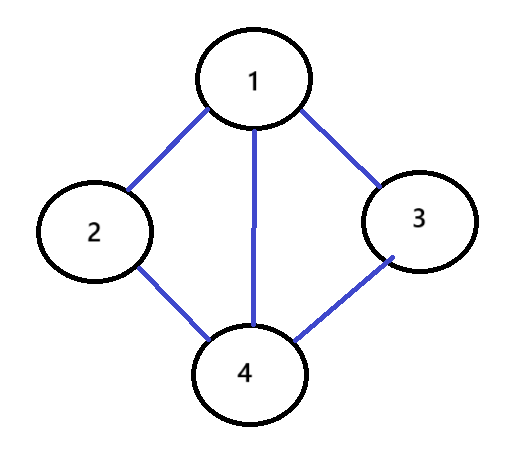
그리고 이 간선을 인접 행렬으로 나타내면 다음과 같습니다.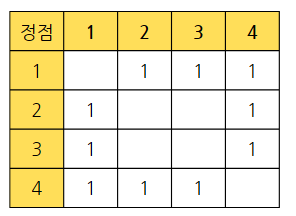
바로 이 행렬을 graph 2차원 배열에 저장하게 됩니다.
graph = new int[n + 1][n + 1]; //정점 번호와 일치시키기 위해 n+1
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine(), " ");
int start = Integer.parseInt(st.nextToken()); //시작 정점
int end = Integer.parseInt(st.nextToken()); //도착 정점
graph[start][end] = 1; //시작-끝 순서 저장
graph[end][start] = 1; //끝-시작 순서도 저장
}이렇게 인접 행렬을 미리 준비해놓고 잠시 뒤에 구현할 dfs, bfs에서 활용합니다.
깊이 우선 탐색 DFS
재귀를 이용한 방법이 있긴 하지만 여기서는 Stack을 이용합니다.
깊이 우선 탐색 DFS, Depth First Search는 한 정점(시작점)에서 한 방향으로 끝까지 탐색한 후 더 이상 이동할 수 없는 정점에 도달하면 방문한 정점들을 되돌아가서 다른 경로를 탐색하는 방법입니다.
자세한 설명은 예전 포스트에서 그림과 함께 확인해주세요.
DFS는 탐색한 정점의 정보를 담기 위해 Stack을 사용합니다. 방문한 정점을 Stack에 push하고 연결된 정점이 없으면 스택에 저장된 정점들을 하나씩 pop해가며 연결된 정점을 확인합니다.
이렇게 pop을 해가면서 스택이 비어있는 상태가 되면 그때가 바로 그래프의 모든 정점을 방문한 상태가 됩니다.
DFS를 정리하면 다음과 같습니다.
- 스택 사용
- 방문한 정점은 push하고 연결된 정점이 더 이상 없으면 pop하면서 이동가능한 정점 탐색
- 스택이 비어있으면 탐색 종료
이 세 가지 정보를 기반으로 DFS를 구현해보겠습니다.
public static String dfs(int n, int m, int v) {
boolean[] visited = new boolean[n + 1]; //방문 정보를 기록할 배열
Stack<Integer> stack = new Stack<>(); //정점 정보를 담을 스택
String result = "";
stack.push(v); //시작 정점이 v로 주어졌기 때문에 스택에 v를 push하고 시작
while (!stack.isEmpty()) { //스택이 빌 때 까지 탐색 반복
int curr = stack.pop(); //현재 탐색 정점을 스택에서 꺼내옴
if (visited[curr]) {
continue; //방문한 적이 있는 정점은 방문 기록 & 스택 push 하지 않음
}
visited[curr] = true; //첫 방문 정점은 방문 기록을 true로 만듦
result += curr + " ";
for (int i = n; i >= 1; i--) { //각 정점을 모두 점검하며 현재 정점과 연결되어있는지 확인
if (graph[curr][i] == 1 && !visited[i]) { //연결되어있고 방문한 적이 없으면 스택에 push
stack.push(i);
}
}
}
return result;
}너비 우선 탐색 BFS
너비 우선 탐색 BFS, Breadth First Search는 한 정점에 인접한 모든 정점들을 한 번씩 방문하고 방문했던 인접 정점의 인접 정점들을 다시 모두 방문해보는 방식입니다.
역시 그림과 함께하는 설명은 이전 포스트를 참조해주세요.
BFS는 Queue를 사용합니다. 방문한 정점을 Queue에 inQueue하고 큐의 정점을 deQueue 하면서 deQueue한 정점에 대해 인접 정점이 있는 지 확인하며 inQueue/deQueue 과정을 반복합니다.
마찬가지로 Queue가 비게 된다면 그래프 탐색이 완료되는 것 입니다.
BFS를 정리하면 다음과 같습니다.
- Queue를 사용
- 한 정점의 인접 정점들을 inQueue
- 하나씩 deQueue하며 해당 정점의 인접 정점들에 대한 inQueue/deQueue 과정을 반복
- 큐가 비면 탐색 종료
이 네 가지 정보들을 기반으로 BFS를 구현해보겠습니다.
public static String bfs(int n, int m, int v) {
boolean[] visited = new boolean[n + 1]; //방문 정보를 기록할 배열
Queue<Integer> queue = new LinkedList<>(); //정점 정보를 담을 큐
String result = "";
queue.offer(v); //시작 정점이 v로 주어졌기 때문에 큐에 v를 인큐하고 시작
visited[v] = true;
while (!queue.isEmpty()) { //큐가 빌 때 까지 탐색 반복
int curr = queue.poll(); //현재 탐색 정점을 큐에서 디큐
result += curr + " ";
for (int i = 1; i <= n; i++) { //모든 정점 한 번씩 순회
if (graph[curr][i] == 1 && !visited[i]) { //연결되어있고 방문한 적 없으면
queue.offer(i); //큐에 해당 정점 인큐
visited[i] = true;
}
}
}
return result;
}전체 코드
전체 코드는 다음과 같습니다.
import java.util.*;
import java.io.*;
public class Main {
private static int[][] graph;
public static void solution() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
graph = new int[n + 1][n + 1];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine(), " ");
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
graph[start][end] = 1;
graph[end][start] = 1;
}
sb.append(dfs(n, m, v)).append("\n");
sb.append(bfs(n, m, v)).append("\n");
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
public static String dfs(int n, int m, int v) {
boolean[] visited = new boolean[n + 1];
Stack<Integer> stack = new Stack<>();
String result = "";
stack.push(v);
while (!stack.isEmpty()) {
int curr = stack.pop();
if (visited[curr]) {
continue;
}
visited[curr] = true;
result += curr + " ";
for (int i = n; i >= 1; i--) {
if (graph[curr][i] == 1 && !visited[i]) {
stack.push(i);
}
}
}
return result;
}
public static String bfs(int n, int m, int v) {
boolean[] visited = new boolean[n + 1];
Queue<Integer> queue = new LinkedList<>();
String result = "";
queue.offer(v);
visited[v] = true;
while (!queue.isEmpty()) {
int curr = queue.poll();
result += curr + " ";
for (int i = 1; i <= n; i++) {
if (graph[curr][i] == 1 && !visited[i]) {
queue.offer(i);
visited[i] = true;
}
}
}
return result;
}
public static void main(String[] args) throws IOException {
solution();
}
}