유클리드 호제법

유클리드 호제법(Euclidean Algorithm)은 두 정수의 최대공약수를 구하는 수학 알고리즘입니다. 두 정수의 최대공약수는 두 정수에서 큰 값을 작은 값으로 나누었을 때, 나머지가 0으로 나누어 떨어지는 값이 최대공약수입니다. 하지만, 보통 한 번의 계산으로는 나누어 떨어지지 않죠. 그래서 큰 값을 다시, 이전에 나온 나머지값으로 나누어 계산합니다. 이 과정을 반복하면 두 정수의 최대공약수를 구할 수 있습니다.

예) 30, 12
30/12 = 2 ... 6
30/5 = 6 ...0
따라서, 두 수의 최대공약수는 6

또는
30의 약수: 1, 2, 3, 5, 6, 10, 15, 30
12의 약수: 1, 2, 3, 4, 6, 12
따라서 두 수의 최대공약수는 6

최대공약수 구하는 과정을 보니 어디를 재귀적으로 처리해야할지 감이 잡히시나요?

유클리드 호제법 구현 (with 최대공약수 구하기)

코드 자체는 간단합니다. 무려 네 줄만에 종료되는 알고리즘 구현입니다. 특히 주목해야할 부분은 두 수를 나눈 나머지가 0이 아닌 경우에 재귀호출을 하게 되는데, 이때 인수 전달과정에 주목해야합니다.

export const euclideanAlgorithm = (num1, num2) => {
    //첫 작동을 제외하고 num1은 큰 수, num2는 두 수를 나눈 나머지입니다.
    
    //나머지가 0이면 현재 몫이자 최대공약수인 num1 반환
    if (num2 === 0) {
        return num1;
    }
    //나머지가 0이 아니면
    else {
        //다시 재귀 호출
        //이때 인수로 num1에는 현재 나머지, num2로는 다시 나눈 나머지를 전달
        return euclideanAlgorithm(num2, num1 % num2);
    }
};

---

서비스: 최소공배수 구하기

재귀 알고리즘의 대표주자인 유클리드 호제법을 통해서 최대공약수를 구해보았습니다. 여기서 서비스로 최소공배수를 구하는 방법도 소개해드리겠습니다. 최소공배수는 다음과 같이 구합니다.

두 자연수 곱 / 최대공약수

두 자연수의 최대공약수로 두 자연수의 곱을 나눠버리면 간단하게 최대공약수를 구할 수 있게 됩니다.

//GCD: Greatest Common Divisor, 최대공약수
const getGCD = (num1, num2) => {
  if (num2 === 0) {
    return num1;
  }
  else {
    return getGCD(num2, num1 % num2);
  }
};

//LCM: Least Common Multiple, 최소공배수
const getLCM = (num1, num2) => {
  return (num1 * num2) / getGCD(num1, num2);
};

위에서 예시를 든 30과 12의 경우 최대공약수는 5, 최소공배수는 60인데요. 위 코드에 숫자를 대입해서 실제로 결과를 확인해보겠습니다.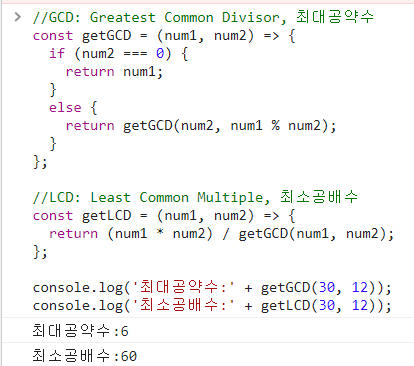

정정
이미지에서 최소공배수 구하는 함수명이 getLCD로 오타가 있습니다. getLCM이 맞습니다.

---

이렇게 이번에는 재귀 알고리즘의 예시로 유클리드 호제법을 소개하면서 최대공약수를 구하는 방식을 알아보았습니다. 거기에 더해 최대공약수를 이용해서 최소공배수를 구하는 방법까지 소개드렸습니다.