트리 Tree
트리(Tree), 나무와 스펠링이 같습니다. 보통 우리가 생각하는 나무는 어떻게 생겼죠? 아래는 넒고 위로 갈수록 좁아지는 형태를 갖고있습니다.
이처럼 트리도 위에서 아래로 갈수록 자료가 많아지는 구조를 가지고 있습니다.
가만보면 여태까지 배운 리스트나 큐, 스택, 데크를 보면 뭔가 통 느낌이 났는데 이건 통이라고 하기 애매한 부분이 있는 것 같다고 생각이 듭니다. 왜냐하면 트리는 계층 관계를 표현하는 자료구조이기 때문입니다.
트리는 사전에 개념들을 익히고 넘어가야하기 때문에 이번 포스트에서는 트리의 소개와 개념들에 대해 알아보자 합니다.
트리의 이해
트리는 비선형, 1:1이 아닌 1:다수의 구조를 가진 자료입니다. 또 자료 사이에 층이 있는 계층적 자료구조입니다. 무슨 이야긴지 모르겠다면 조직도를 보면 이해가 되실겁니다.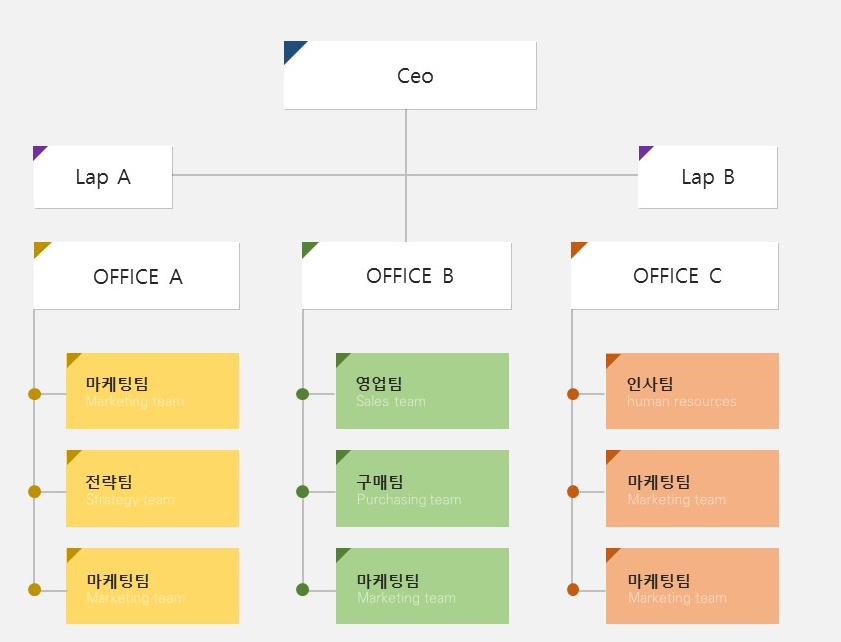
제일 위에 CEO가 있고 그아래 여러 사무실이, 사무실 밑에 또 n개의 세부팀까지 연결되어있습니다. 이런식으로 구성되있는 것을 트리 구조 라고합니다. 하나의 ceo아래 5개의 자료가있고 하위 오피스에 3개의 자료가 있습니다. 이렇게 1:다수의 균등하지 않은 비선형 구조입니다.
자 그럼 트리가 어떻게 생겼는지 보고 구성을 살펴보겠습니다.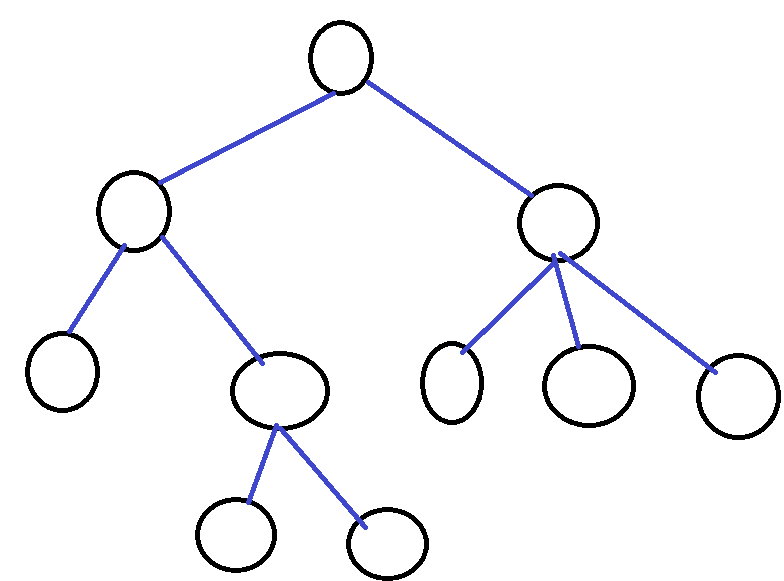
트리의 구성
트리에서 제일 먼저 눈에 띄는 것이 있는데. 동그라미와 선들 입니다. 동그라미는 구조에 저장된 자료입니다. 이 자료들을 노드라고 하고, 이 노드들을 잇고 있는 선을 간선이라고 합니다.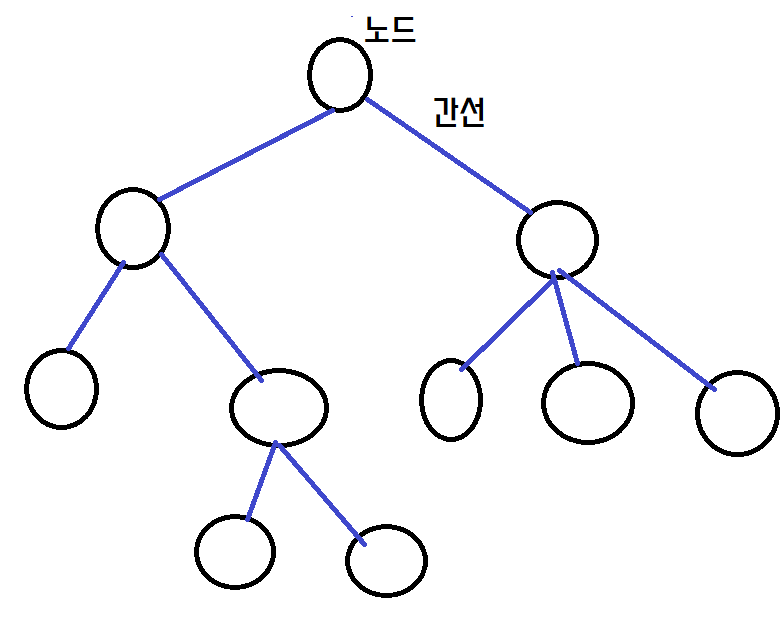
맨 위의 노드는 루트(root)라고 합니다. 이 루트 노드가 트리의 시작입니다. 또한 레벨0이라고 하며, 이는 노드가 한 칸 씩 내려갈수록 레벨이 1증가합니다. 트리가 완성됐을때 레벨의 수를 가장 높은 레벨로 보고 그 숫자를 트리의 높이 라고합니다. 다시 말해 트리의 높이 == 트리의 레벨입니다.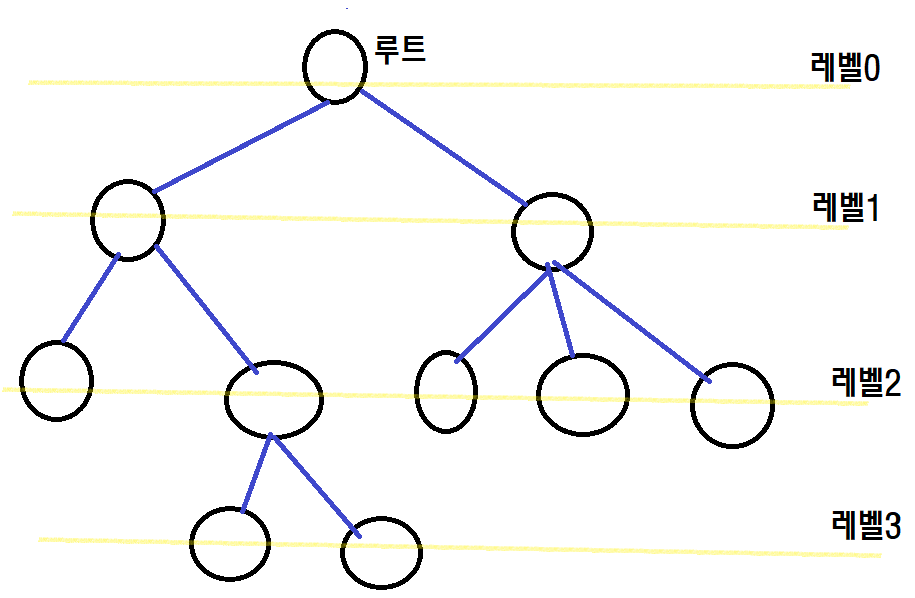 
연결되어있는 노드에서 상위에 있는 노드를 부모 노드, 그 하위에 있는 노드를 자식 노드라고 합니다. 이때 자식 노드에서 같은 부모를 갖고 있는 노드 끼리는 형제 노드 라고 합니다.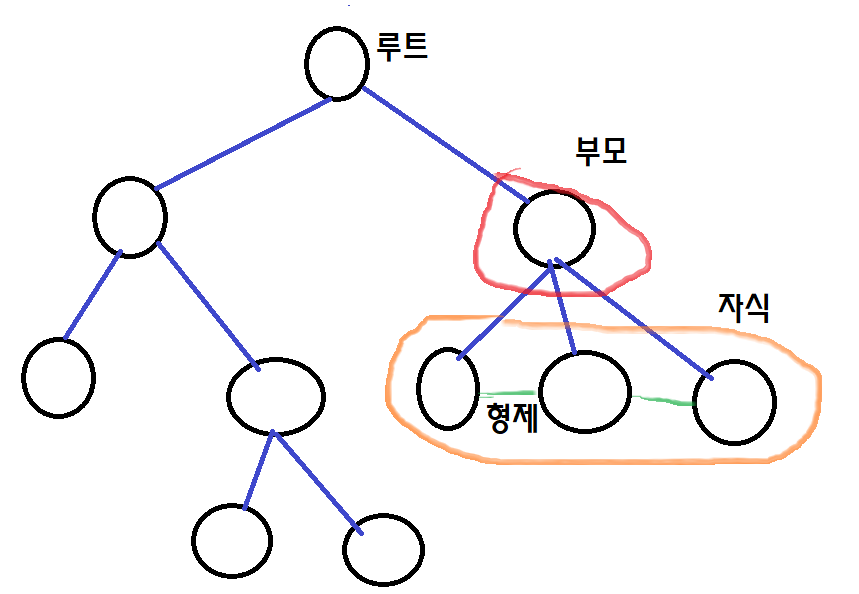
어떤 한 노드에서 루트 노드 까지 가는 경로에 있는 노드들을 조상 노드라고 합니다.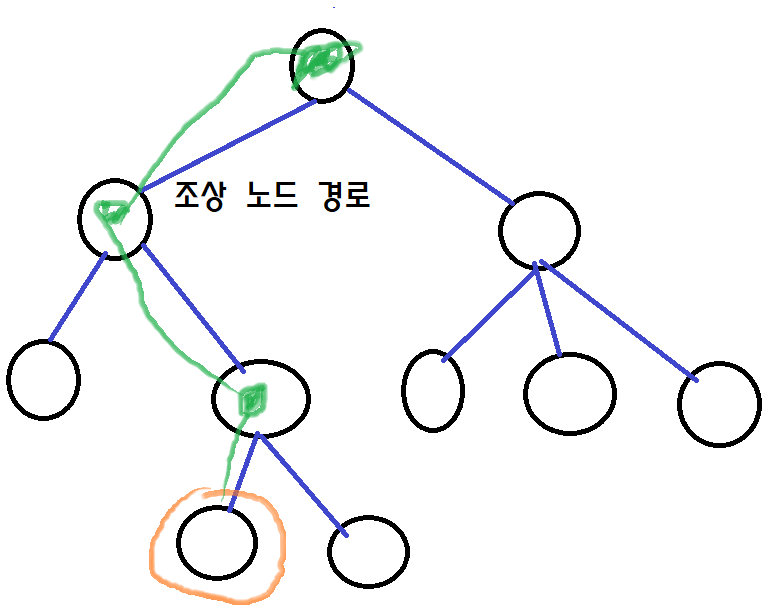
한 노드의 하위 노드들은 따로 빠져나와서 다른 트리를 구성할 수 있습니다. 이처럼 구성할 수 있는 트리는 자식 노드 수 만큼이 되며 이 트리들을 서브 트리라고 합니다.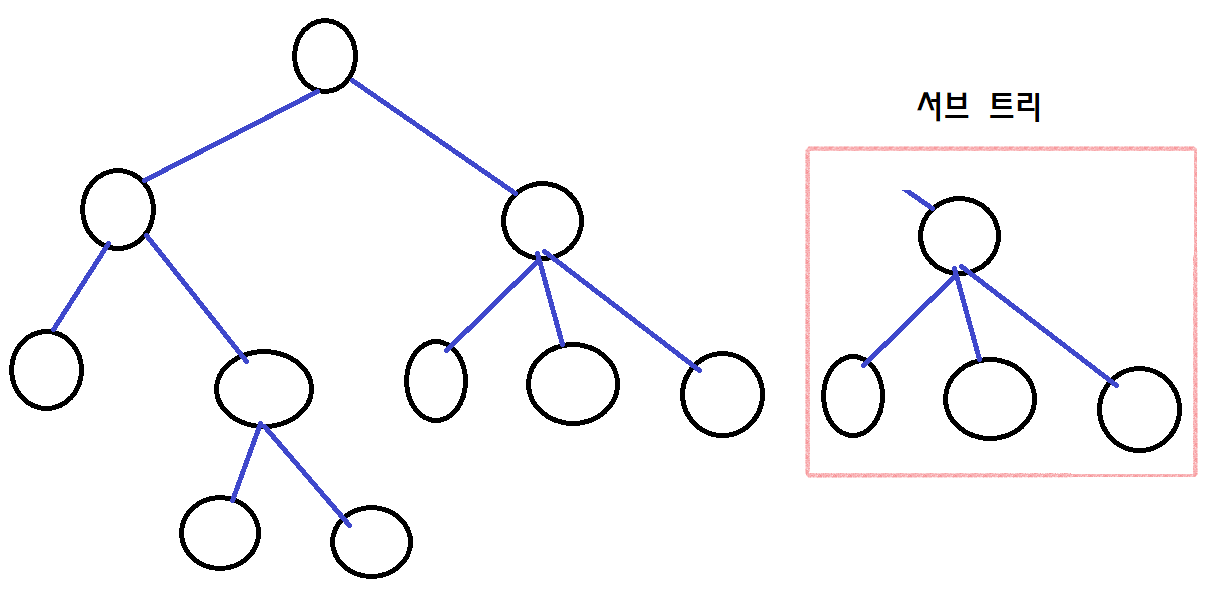
한 노드에서 서브 트리가 생기는 갯수를, 좀 더 쉽게 말해 한 노드의 자식 노드 수를 차수(degree)라고 합니다. 예를 들어 위 트리의 루트 노드는 자식이 두개 이므로 차수는 2가 되고, 서브 트리의 자식 노드 수는 3이므로 차수는 3이 됩니다.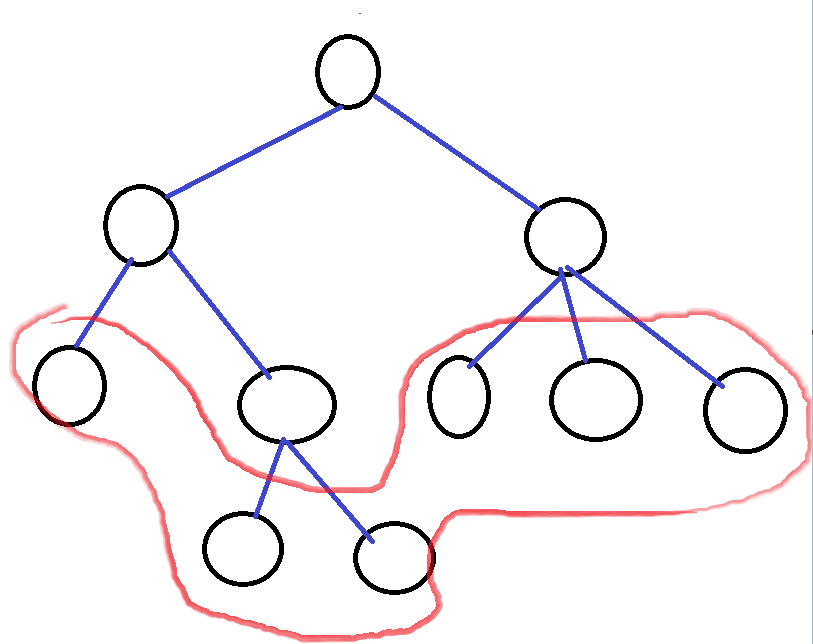
빨간펜으로 표시된 자식 노드가 없는(= 차수가 0인) 노드들은 단말 노드, 리프(leaf) 노드 라고 합니다. 이 외에 차수가 1 이상인 노드들은 내부 노드 라고 합니다.
트리에 이처럼 노드마다 다양한 차수를 가지고 있는데 이 중에서 제일 큰 차수가 트리의 차수가 됩니다. 위 그림에서 최고 차수는 3이므로 이 트리의 차수는 3이됩니다.
마지막으로 노드의 높이라는 개념이 있습니다. 노드의 높이는 루트 노드에서 해당 노드까지 간선의 갯수를 의미합니다.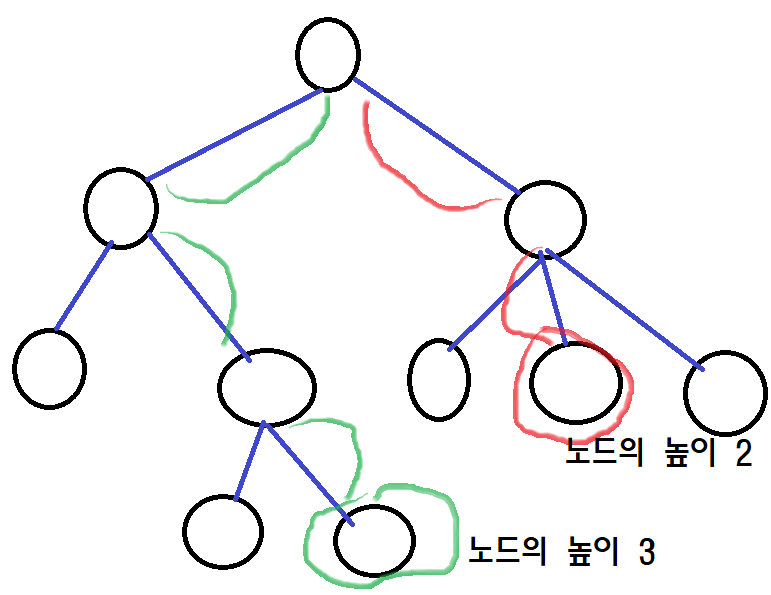
추가적으로 트리 여러개의 집합을 포레스트(Forest)라고 합니다.
