99클럽 코테 스터디 6일차 TIL Range sum of bst

Range sum of bst

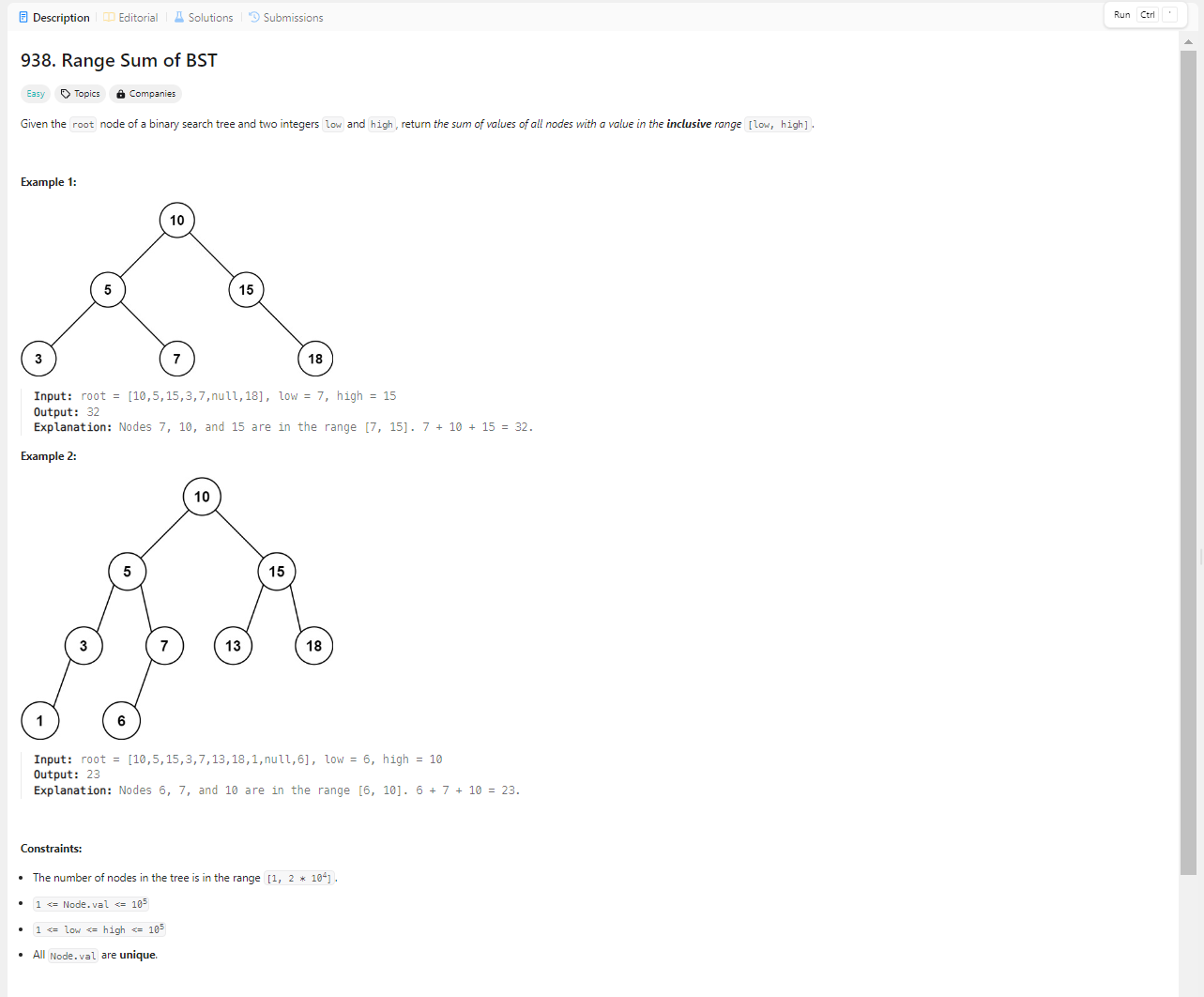
• 문제 풀이

  1. binary search tree인것 확인
  2. node가 null일때 return 0을 한다.
  3. 현재 노드의 값이 주어진 범위안에 있는지 확인
  4. 범위 보다 작으면 트리 자식 노드의 오른쪽 값을 기준으로 rangeSumBST 재귀함수 호출
  5. 범위 보다 크면 트리 자식 노드의 왼쪽 값을 기준으로 rangeSumBST 재귀함수 호출
  6. 범위 안에 해당하면 해당 트리 노드의 현재 값을 더한 후 자식 노드의 왼쪽 오른쪽 둘다 rangeSumBST 재귀함수를 호출한다.

• 풀이 소스

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rangeSumBST(TreeNode root, int low, int high) {
        if(root == null){
            return 0;
        }
        if(root.val < low){
            return rangeSumBST(root.right, low, high);
        }
        if(root.val > high){
            return rangeSumBST(root.left, low, high);
        }
        return root.val + rangeSumBST(root.right, low, high) + rangeSumBST(root.left, low, high);
        
    }
}

• 오늘의 회고

  • 문제 시도 및 해결

    • binary search tree의 단어가 생소했다.
    • 문제 예제를 봐도 무슨 소리인지 이해 못했다.
    • binary search tree에 대해 검색해 봤다.
    • 이진 탐색 트리에 대해 알 수 있었으며 재귀함수를 사용하라는 힌트를 얻었다.
    • 트리 현재 값과 자식들의 값에 대해 범위 조건을 따져 재귀함수로 return값을 가져올 수 있었다.
    • 마지막 노드에 도달했을때 null값 체크도 해야했다.

  • 학습 내용

    • binary search tree(이진 탐색 트리)에 대해 공부할 수 있었다.

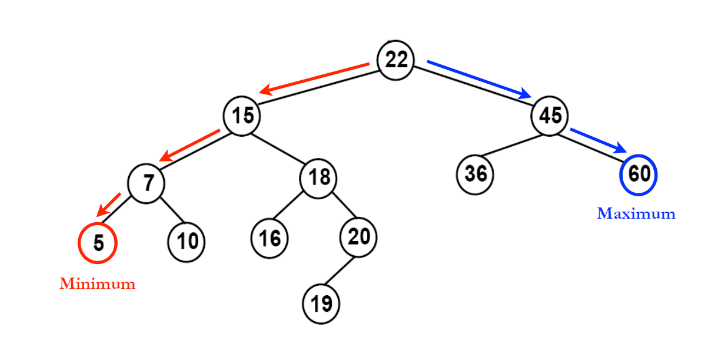
  • binary search tree(이진 트리 기반의 탐색을 위한 자료구조)

    1. 모든 원소의 키는 유일한 키를 가진다.
    2. 왼쪽 서브 트리 키들은 루트 키보다 작다.
    3. 오른쪽 서브 트리의 키들은 루트의 키보다 크다.
    4. 왼쪽, 오른쪽 서브 트리 모두 이진 탐색 트리이다.

  • binary search tree 그림

    

  • 다음 배울것

    • 부족한 자바 문법
    • 스프링 공부
    • 알고리즘
    • 코테 문제 풀이