EECS498-007 Lecture 21 | Reinforcement Learning

shyoon·2025년 3월 8일

EECS498-007 딥러닝 머신러닝 컴퓨터비전

EECS 498-007

목록 보기

13/13

✍ 해당 시리즈 포스팅은 미시간 대학의 EECS 498-007 강의 내용을 정리한 글입니다.

Reinforcement Learning

오늘은 이전의 학습 paradigm과는 다른 머신 러닝 모델의 세 번째 학습 paradigm인 reinforcement learning(강화 학습)에 대해 다룬다.

강화 학습은 세상과 상호 작용할 수 있는 어떤 agent를 구축하는 것이다. 이는 특정 환경에서 액션을 취할 수 있고, 이에 대한 보상을 얻게 된다. 이러한 보상을 최대화하는 것이 학습의 목표가 된다.

다음과 같이 agent와 environment(환경)가 주어지게 되는데, 우리는 환경에 대한 제어권은 가지지 못하고, agent를 제어하여 환경과 상호작용 하도록 한다.

먼저 환경은 agent에게 일부 state인 $s_t$ 를 제공하는데, 이는 세계의 현재 상태를 캡슐화한다. 우리가 로봇을 만들고 있다면 이러한 state는 로봇이 현재 보고 있는 이미지 등이 될 수 있다.

Agent는 이런 state를 받아서, 현실 세계에서 무엇을 하고 있는지, 또는 주변에 무엇이 있는 지에 대한 어느 정도의 이해를 얻고 작업을 수행하여 환경과 다시 통신한다.

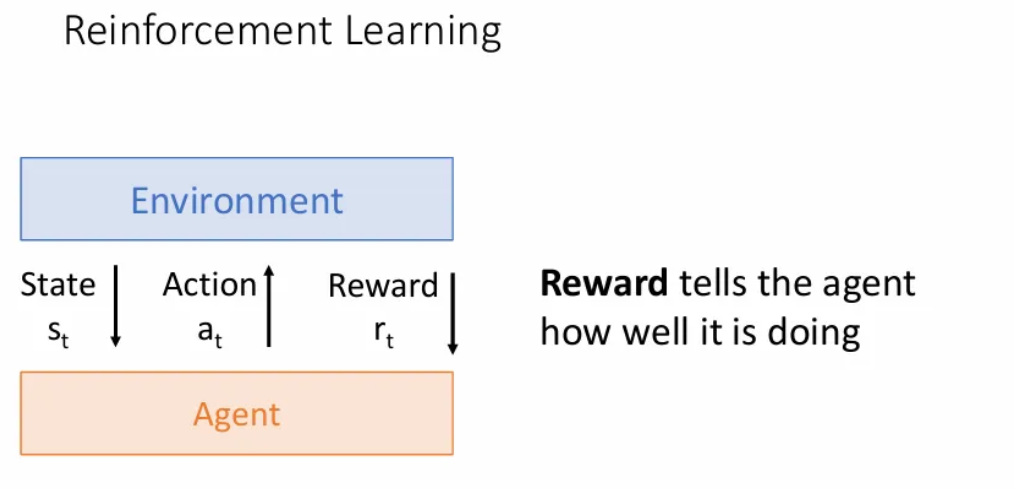
그리고 환경은 이러한 행동에 대한 보상을 보낸다. 이는 해당 시점에서 agent가 얼마나 좋은 action을 취했는 지에 대한 지표가 된다.

보상의 형태는 예를 들면, 물건을 배달하는 agent의 경우 해당 시점에서 얼마나 돈을 벌었는 지 등이 될 수 있다.

그리고 이러한 과정을 단일 time step이 아닌, 시간이 지남에 따라 전개되고, 환경과 agent는 장기적인 상호작용을 하게 된다.

Agent의 action으로 인해 환경이 변화했고, 이러한 새로운 state $s_{t+1}$ 을 다시 agent에게 보내는 과정을 반복하게 된다.

Example

강화학습으로 접근 가능한 대표적인 예시로는 cart-pole problem을 들 수 있는데, 1차원 트랙에서 카트를 앞 뒤로 움직일 수 있는 일종의 막대를 조종하는 문제이다.

State: 카트의 각도, 카트의 $x$ 좌표, 속도 등이 될 수 있다.
Action: 이동하는 카트에 적용하는 수평 힘
Reward: 막대가 균형을 이루면 1, 막대가 떨어지면 0으로 설정

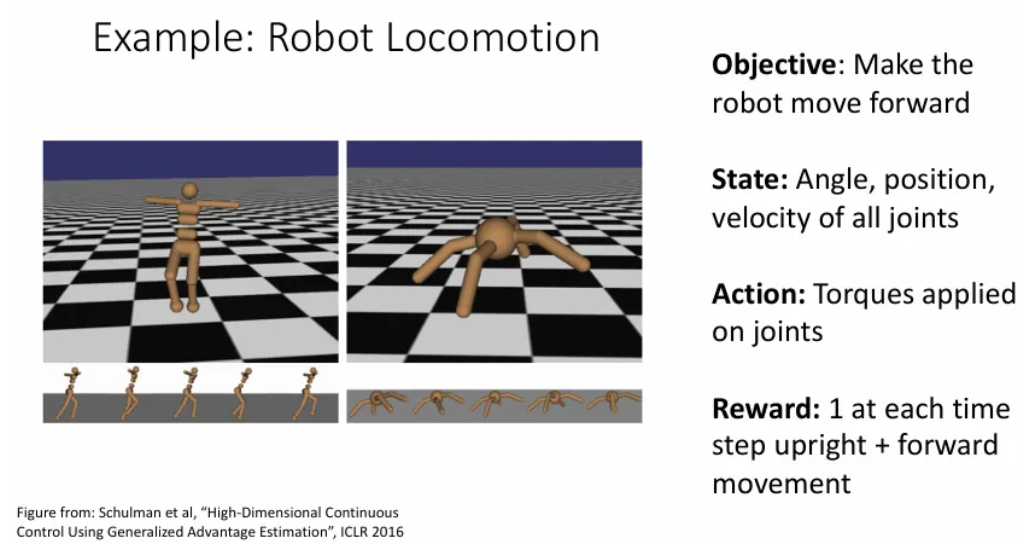
두 번째 예시는 Robot Locomotion으로 로봇이 앞으로 나아가게끔 하고자 하는 목표이다.

State: 각도, 위치, 모든 관절의 속도 등이 될 수 있다.
Action: 관절에 적용하는 돌림힘
Reward: 로봇이 잘 서있고, 앞으로 나아갈 때 마다 1을 보상

세 번째 예시는 Atari game에서 높은 점수를 기록하게끔 하는 목표이다.

State: 게임 스크린의 raw pixels
Action: 상하좌우로 움직이는 game controls
Reward: 각 step마다 게임의 점수가 오르는지/줄어드는지

이 경우엔 우리에게 주어지는 state는 일부 정보만을 포함하게 되는데, 예를 들면 갤러그같은 게임에서는 다음 미사일이 어디서 나오는지에 대한 정보는 미리 알 수 없고, 현재 화면에서의 상황만 주어질 수 있다.

이번엔 agent와 agent가 경쟁하는 대화형 게임(e.g. 바둑)에서도 적용될 수 있는데, 우리의 agent가 상대 agent를 이기도록 목표를 세운다.

State: 모든 바둑돌의 위치
Action: 어디에 다음 바둑돌을 내려놓지 결정
Reward: 마지막 턴에서 이기면 1, 지면 0

Reinforcement Learning vs Supervised Learning

강화 학습을 지도 학습과 비교하면 마치 환경(environment)은 dataset처럼 생각할 수 있고, agent는 모델처럼 비슷하게 생각할 수 있다.

처음에 환경으로부터 state를 얻는 과정은 dataset에서 input $x$ 를 입력 받는 것과 같다.
그리고 agent가 이에 대한 action을 취하는 것이 지도 학습 모델이 예측 $y$ 를 출력하는 것과 유사하다.
마지막으로 결과에 대한 보상을 주는 것은 지도 학습에서 loss를 출력하는 것과 유사하다.

하지만 두 방법은 근본적인 차이가 있다.

Stochasticity (확률성)

강화 학습 설정에서는 모든 것에 noise가 있을 수 있으므로 우리가 얻는 state는 noisy하거나 해당 장면에 대한 정보가 불완전할 수 있다.
Agent가 얻는 보상 또한 노이즈가 있거나 불완전할 수 있다.
우리가 얻는 $t_1$ 에서 $t_2$ 로의 환경의 transition 또한 noisy할 수 있다. 이는 알려지지 않은 non-deterministic한 함수일 수도 있다는 것을 의미한다.

예를 들면 강화 학습에서는 정확히 같은 작업을 수행하더라도 다른 time step에서는 다른 보상을 받을 수 있고, agent는 이를 다루는 법을 학습해야 한다.

Credit assignment

위 바둑 게임에서 본 것 처럼, agent가 각 time step에서 얻는 보상이 해당 step에서 수행한 작업을 정확히 반영하지 않을 수 있다.
Time step t+1 시점에서 얻는 보상이 아주 오래전에 취한 행동의 결과일 수도 있다.

예를 들면 커피를 배달하는 로봇이 커피 배달을 마친 시점에서 보상을 얻지만, 이는 그 전까지의 일련의 모든 과정의 상호작용으로 얻게되는 것이다.
반면 지도 학습에서는 바로바로 손실이 발생하고, 이는 순간 예측이 얼마나 좋았는 지를 알려준다.

Nondifferentiable (미분불가)

강화 학습의 큰 문제 중 하나로, 모든 것이 미분 불가능하다. 즉, action에 대한 reward의 변화량을 구할 수가 없다.
강화 학습에서는 이러한 미분 불가능한 상황을 처리해야 한다.

Nonstationary (비정상성)

Agent가 보는 state는 agent가 이전 time step에서 수행한 작업에 따라 달라지게 된다.
결국 이에 따라서 agent는 이전과는 다른 새로운 환경에 빠지게 되고, agent는 이러한 변화에 적응하기 위해 계속해서 새로운 정보를 받아서 학습해야 한다. 즉, 데이터의 분포가 계속해서 바뀐다고 생각하면 될 듯.

예시로, 커피를 배달하는 로봇이 정해진 장소의 특정 사람에게 커피를 주는 작업에 능숙해졌는데, 이를 잘 수행함에 따라 사람들이 로봇에게 길 건너 커피숍에서 커피를 가져오라고 요청할 수 있다.

이러한 nonstationary problem은 GAN에서도 나타난다.

Markov Decision Process (MDP)

Decision process에 마르코프 성질을 적용한 모델로 이는 현재 상태만 알아도 다음의 state와 보상을 알 수 있다는 것이다.

총 5가지 요소로 정의된다.

S: 환경의 가능한 모든 상태 집합
A: Agent가 취할 수 있는 모든 action 집합
R: Agent가 state에서 특정 action을 취했을 때 받을 수 있는 보상의 분포
P: 특정 state에서 특정 action을 취했을 때, 다음 state로 이동할 확률
$\gamma$ : 지금 당장 보상을 받는 것과 미래에 보상을 받는 것을 각각 얼마나 선호할 지 조정. 일종의 인플이션 계수 같은 것. gamma가 0이면 직후 보상에만 관심을 갖고, 1이면 미래 시점의 보상도 현재만큼 중요하게 생각함

이 때 agent는 $\pi$ 라는 policy를 실행하면 현재 state에 따른 action을 선택할 확률 분포를 얻는다.

목표는 마지막에 쌓인 보상을 최대화하는 $\pi^*$ 를 찾는 것

t=0 시점에서 환경은 초기 state인 $s_0$ 을 초기 state에 대한 일부 사전 분포에서 샘플링한다.
t=0 부터 해서 학습이 끝나는 시점까지 아래 과정을 반복한다.
- Agent는 $s_t$ 에 따른 조건부 policy $\pi$ 에서 action $a_t$ 를 선택
- 환경은 $R(r|s_t, a_t)$ 를 따르는 보상 $r_t$ 를 샘플링
- 환경은 $P(s|s_t, a_t)$ 를 따르는 다음 state $s_{t+1}$ 을 샘플링
- Agent는 reward $r_t$ 와 다음 state $s_{t+1}$ 을 받음

Markov decision process의 간단한 예시는 위 grid world이다.

목표를 가능한 적은 움직임으로 terminal states 중 하나에 도달하고자 할 때, A, S, R은 다음과 같다.

Actions: {위, 아래, 오른쪽, 왼쪽}
States: {(0,0), (0,1), (0,2), (0,3), (1,0), (1,1), (1,2), (1,3), (2,0), (2,1), (2,2), (2,3)}
Reward: 이동을 한 번 할 때마다 -1

왼쪽의 경우엔 좋지 못한 policy가 되고, 오른쪽의 경우가 최적의 policy가 될 수 있다.

이렇듯 강화학습의 목표는 보상을 최대화하는 최적의 policy인 $\pi^*$ 를 찾는 것인데, 초기 state, transition probabilities, rewards 등에서 너무 랜덤성이 강하다는 문제가 있다.

따라서 보상들의 합의 기댓값을 최대화하는 policy $\pi^*$ 를 찾는 방법을 사용하게 된다.

Value Function and Q Function

Policy $\pi$ 를 따르면 sample trajectory(궤적?) 이 생긴다.

Value Function

Value function( $V^{\pi}(s)$ )은 $s$ 에서 시작해서 policy $\pi$ 를 따를 때 얻을 수 있는 미래 보상의 총 합에 대한 기댓값으로, 각 states에서 우리가 얼마나 잘 하고 있는 가에 대한 지표가 된다. 따라서 이 함수는 policy $\pi$ 에 의존적이게 된다.
이러한 V가 높다면 해당 state에서 policy $\pi$ 로 작업할 때 미래에 많은 보상을 얻을 수 있다.

Q Function

하지만 이렇게 직관적인 value function에 비해서, Q function은 학습 알고리즘에 훨씬 더 수학적으로 편리하다.
Action-value function인 $Q$ 는 특정 state $s$ 에서 특정 action $a$ 를 선택하고, 그 뒤로 policy $\pi$ 까지 따를 때 얻을 수 있는 미래 보상의 기댓값을 의미한다.

Value function은 해당 state에서 시작하여 policy와 V를 실행할 때 얻을 수 있는 보상의 기댓값을 통해, 현재 state가 얼마나 좋은지를 알려주고,

Q function은 state-action pair로 시작하여 policy를 따를 때 남은 경로 동안 해당 정책을 따른다고 가정할 때 얻을 수 있는 보상의 기댓값을 통해 initial state-action pair가 얼마나 좋은지 알려준다고 보면 될 것 같다.

Bellman Equation

이러한 함수들의 최적을 구하기 위한 방정식이 bellman equation이다.

만약 $Q^*(s,a)$ 가 최적의 policy $\pi$ 에서의 Q function이라고 할 때, 이는 state $s$ 에서 action $a$ 를 취할 때 최대의 기대 보상을 준다.

여기서 $Q^*$ 는 $\pi^*$ 를 encoding하고, $\pi^*$ 는 모든 state에 대해서 취할 수 있는 모든 최상의 가능한 행동이 무엇인지 알려준다. 이를 통해 나머지 시간 동안 보상을 최대화할 수 있다.

이러한 Q function의 경우에는 state와 action을 모두 취하도록 정의되고, Value function과는 달리 더이상 policy function에 대해 생각할 필요가 없기 때문에 많이 쓰인다.

이제 Bellman equation의 직관은 state $s$ 에서 action $a$ 를 취하면 이 둘에만 의존하는 즉각의 reward인 $r$ 을 얻는데, 그 time step 이후 다음 state인 $s'$ 로 이동하고, $s'$ 에 도착한 뒤부터 얻을 수 있는 최대 보상이 $max_{a'}{Q^*(s', a')}$ 가 된다는 것이다.

첫 번째 state에서 최적의 action을 취한 후에 그 다음 action은 또 다시 $\pi^*$ 에 따라 이루어진다. 그리고 $\pi^*$ 는 $Q^*$ 로 인코딩되므로 이는 좋은 재귀 관계가 되고, 최적의 $Q^*$ 를 바로 다음 time step에서 얻는 보상에 따라 정의할 수 있다는 것이다.

어쨌든 이러한 Bellman Equation을 만족하는 $Q(s,a)$ 를 찾는다면, 그것이 바로 optimal $Q^*$ 이 된다는 것이고, 이러한 $Q$ 를 찾고자 해야한다.

랜덤 Q function에서 시작하여 다음 모든 time step에서 bellman equation으로 Q function을 업데이트하는 규칙을 사용한다.

즉, 다음 $Q$ 를 업데이트 할 땐 즉시 보상인 $r$ 과, 다음 step에서 최대 보상을 내는 action으로 $Q$ 를 업데이트하게 되고, 결국 $Q$ 가 $Q^*$ 에 수렴하도록 만든다.

하지만 이런 bellman 방정식을 통해 최적의 $Q^*$ 로 수렴하기 위해서는 모든 (state, action) 쌍에 대한 Q를 계산해야하고, 이러한 쌍이 무한한 경우 곤란하다.

따라서 bellman 방정식을 loss로 하는 neural network를 통해 $Q(s,a)$ 를 근사하는 방법으로 발전하게 된다.

Deep Q-Learning

이제 bellman 방정식과 매개변수가 $\theta$ 인 신경망을 학습시켜서 최적의 $Q^*$ 에 근사하도록 한다.

해당 신경망에서는 네트워크가 잘 동작한다면 네트워크의 출력이 bellman 방정식을 만족할 것이므로 state와 action을 입력하여 얻은 $Q(s, a; \theta)$ 와, bellman 방정식을 통해 $y_{s,a,\theta}$ 를 얻고, $Q(s, a; \theta)$ 와 $y_{s,a,\theta}$ 의 차이의 제곱을 loss로 설정하여 학습이 진행된다.

하지만 위 방법 역시 $Q(s,a)$ 에 대한 target이 현재 weight $\theta$ 에 의존한다는 nonstationary(비정상성) 문제를 갖게 되고, 학습을 위한 데이터 batch를 어떻게 샘플링하는가에 대한 문제도 발생한다.

Policy Gradients

Q learning과 다르게, policy gradients는 최적의 policy자체를 학습하는 방식이다. 이는 state $s$ 에서 어떤 action $a$ 를 취할지를 확률로 알려준다고 보면 된다.

목적 함수는 해당 policy $\pi_\theta$ 가 주어졌을 때 future rewards의 기댓값이 되고, $\theta$ 는 해당 목적 함수를 최대화하는 방향으로 gradient ascent를 통해 업데이트 된다.

물론 해당 식이 미분 불가하기 때문에 문제가 발생하고, 이를 해결하기 위해서는 수학적 trick이 필요하다.

확률 분포 $p_\theta$ 에 따라 샘플링 된 $x$ 의 입력에 대한 $f$ 기댓값을 작성하고, $\theta$ 에 대한 변화량을 계산하는 방법이다.

여기서 $x$ 는 trajectory(궤적)이 되고, $p_\theta(x)$ 는 policy $\pi_\theta$ 에 따라 $x$ 가 나올 확률이며, $f(x)$ 는 그 경로에서 받은 총 보상이 된다.

일단 먼저 기댓값의 적분 정의를 확장한다. 하지만 $\theta$ 확률 밀도 함수 $p_\theta(x)$ 의 미분을 직접 수행하기엔 어려울 수 있다.

그리고 위의 log derivative trick에 따라 $\frac {\partial}{\partial \theta} p_{\theta}(x)$ 는 $p_\theta(x)\frac {\partial}{\partial \theta}logp_\theta(x)$ 로 변환되고, 이제 확률 밀도 함수에 대한 미분을 계산하지 않아도 된다.

값을 대체하면 $\frac {\partial J}{\partial \theta}$ 는 위와 같이 바뀔 수 있고, 이제 이 식은 확률 분포 $p_\theta(x)$ 에 대한 기댓값으로 표현되므로, 실제로 샘플링을 통해 근사할 수 있다.

그렇다면, 이제 목표는 주어진 state $s$ 에서 어떤 action $a$ 를 선택할 확률 분포를 출력하는 network $\pi_\theta$ 를 학습하는 것이 목표가 된다.

Policy $\pi_\theta$ 를 따를 때 발생하는 state 및 action의 시퀀스를 $x$ 로 정의할 때, 이는 확률적으로 결정되므로 $x$ ~ $p_\theta(x)$ 로 표현될 수 있다. 즉, policy $\pi_\theta$ 를 따를 때 나오는 데이터의 확률 분포를 $p_\theta(x)$ 라고 한다.

이제 Markov decision process의 정의를 사용하여 trajectory $x$ 를 관찰할 확률이 무엇인지 쓸 수 있고, 또한 이에 대한 log 확률도 볼 수 있다.

하지만 빨간색으로 표시된, 현재 state $s_t$ 와 action $a_t$ 를 취했을 때 다음 상태 $s_{t+1}$ 이 나올 확률인 transition probabilities는 우리가 직접 계산할 수 없다.

반면 파란색 부분은 우리 모델이 취하는 action probabilities는 계산 가능하다.

이제 이 로그 확률을 $\theta$ 에 대한 미분을 취하면 빨간 term은 $\theta$ 와 관련이 없으니 사라지게 되고, 이제 policy probabilities인 $\pi_\theta(a_t | s_t)$ 의 미분만 포함되고, 이는 계산 가능하다.

이제 이 값을 아까 유도했던 기댓값의 괄호 안에 그대로 대체하게 되면 위와 같이 표현될 수 있다.

그리고 이렇게 얻은 최종 기댓값은 policy $\pi_\theta$ 에 따라 샘플링한 trajectory $x$ 에 대한 기댓값을 취하는 것을 의미한다. 따라서 우리는 환경에서 해당 policy를 실행하고 trajectory $x$ 를 수집해서 이를 얻을 수 구할 수 있다.

그리고 $f(x)$ 는 trajectory $x$ 를 관찰할 때 얻어지는 보상이므로 이도 관찰 가능하다.

마지막 term은 model weights $\theta$ 에 따른 예측된 action scores의 gradient가 되고, 이를 통해 backpropagation이 가능하게 된다.

따라서 policy gradients를 적용하는 순서는 다음과 같다.

random weights $\theta$ 초기화
환경에서 policy $\pi_\theta$ 를 일정 time step동안 실행하여 데이터 수집( $x$ , $f(x)$ )
모든 데이터를 수집한 후 위에서 구한 기댓값에 대입하여 gradient 계산
Gradient ascent를 적용
Step 2로 돌아가서 과정 반복

그리고 이에 대한 직관은, 만약 보상 $f(x)$ 가 높다면 우리가 취하고 있는 action이 좋다는 것이므로 probability를 늘려야 하고, 반대로 $f(x)$ 가 낮다면 우리가 취하는 action의 확률을 낮춰야 한다.

하지만 이러한 policy gradients 방법은 데이터를 최대한 많이 수집해야 한다.

Other Approaches

Q learning과 Policy gradients 외에도 다양한 방법들이 있다.

Actor-Critic
- Actions를 예측하는 actor와 이러한 action을 취함으로써 얻을 수 있는 미래 보상을 예측하는 critic을 학습 (Q Learning과 유사)
Model-Based
- 환경의 state transition function을 명시적으로 학습하여 환경 모델을 구축하고 planning을 통해 최적의 행동을 결정
Imitation Learning
- 지도 학습 방식으로, experts의 행동 데이터를 수집해서 그 행동을 모방하도록 학습
Inverse Reinforcement Learning
- 환경에서 experts의 데이터를 수집하고, reward function을 역으로 추론
- 이후 강화 학습을 통해 최적의 policy를 학습
Adversarial Learning
- Action이 가짜인지 진짜인지(expert로 부터 나온 action인지 아닌지)를 판별하는 discriminator를 속이도록 학습

Case Study

이러한 강화 학습을 통해 바둑이나 체스 등에서 매우 강력한 모델들을 학습하였고, 해당 모델들은 모두 인간 챔피언들을 능가하였다.

Stochastic Computation Graphs

또한 미분 불가한 요소들로 신경망을 학습시키는 방법도 있다.

예시로, 회색 CNN 네트워크를 통해 나머지 세 가지 CNN 모델 중 어느 것을 사용하여 분류를 수행하여야 하는지 알려준다. 결과로 초록색 네트워크가 선택되었고, 이 초록색 네트워크를 통해 분류를 수행하고 그 loss를 보상으로써 활용하는 방법이다.

Stochastic Computation Graphs: Attention

이번엔 이미지 캡셔닝에서 attention을 활용할 때, 기존의 soft attention과 달리 각 timestep마다 정확히 하나의 spatial location의 feature를 선택해서 policy gradsients로 학습시키는 hard attention 방법도 있다.