데이터 군집화 - K-Means

shyoon·2023년 6월 30일

머신러닝

목록 보기

6/11

✍K-Means 군집화란?

중심기반 분리형 군집화의 한 방법으로 데이터를 K개의 겹치지 않는 군집으로 분리하는 알고리즘

각 군집은 하나의 중심(centroid)를 가짐
각 개체는 가장 가까운 중심에 할당되며, 같은 중심에 할당된 개체들이 모여 하나의 군집 생성
사전에 군집 수 K를 정해주어야 함 $X = C_1 \cup C_2 \cup ... \cup C_k, \ \ C_i\cap C_j = \phi, \ \ i \ne j \\\ \\\ \\\ argmin_C \ \sum_{i=1}^K \sum_{x_j\in C_i} \vert\vert x_j - c_j \vert\vert^2$

알고리즘 순서

K개의 초기 군집 중심 설정
모든 개체를 가장 가까운 군집 중심에 할당하여 군집 구성
할당된 개체들을 이용하여 군집 중심을 업데이트
종료 조건: 모든 군집 중심들의 위치가 변하지 않고, 모든 개체의 군집 할당 결과에 변화가 없을 때

※ 초기 군집 중심은 실행할 때마다 달라서 분석 결과가 상이할 수 있다.

(예시 그림)

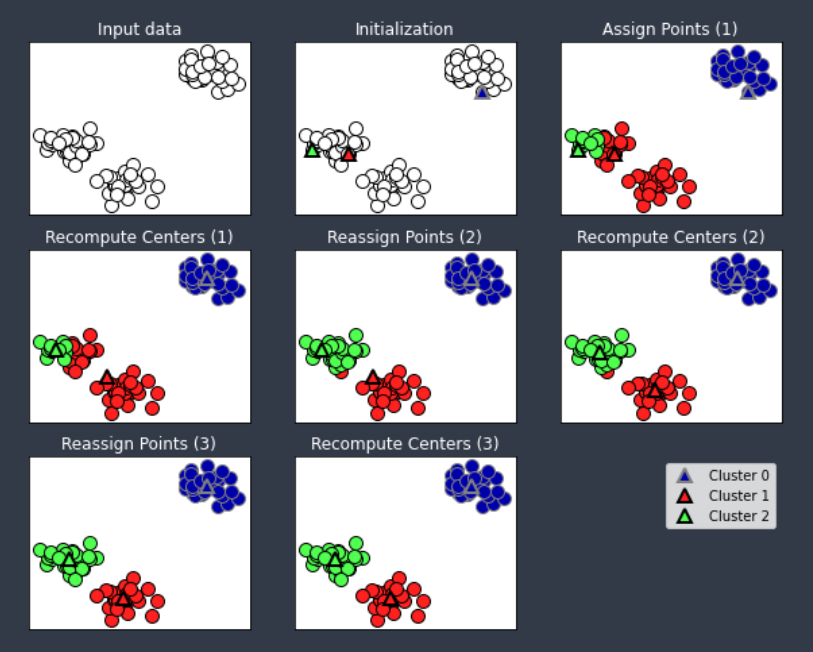
위 그림은 mglearn에서 제공하는 사전에 K를 3으로 설정하고 K-Means를 실행한 예시 그림이다. 초기 군집 중심은 랜덤으로 배치된다. iter이 돌 때마다 군집 중심과 군집 개체들은 업데이트 되고 있고, 둘 다 변하지 않는 시점에서 종료되는 것을 확인할 수 있다.

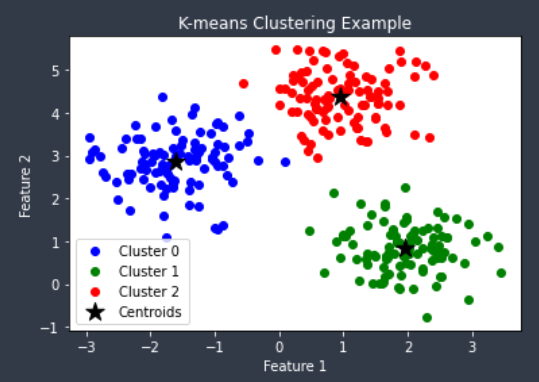
아래는 예시 코드와 결과이다.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

# make_blobs를 사용하여 원형 군집 데이터 생성
X, y = make_blobs(n_samples=300, centers=3, cluster_std=0.6, random_state=0)

# K-means 알고리즘으로 군집화
kmeans = KMeans(n_clusters=3, random_state=0)
kmeans.fit(X)

# 군집 중심 확인
centroids = kmeans.cluster_centers_

# 군집화 결과 시각화
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k']
for label in set(kmeans.labels_):
    color = colors[label % len(colors)]
    cluster_points = X[kmeans.labels_ == label]
    plt.scatter(cluster_points[:, 0], cluster_points[:, 1], c=color, label=f'Cluster {label}')

plt.scatter(centroids[:, 0], centroids[:, 1], marker='*', c='k', s=200, label='Centroids')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('K-means Clustering Example')
plt.legend()
plt.show()