신경망 학습

데이터 주도 학습

머신러닝과 딥러닝의 중요한 차이점(엄밀히 따지면 딥러닝이 기계학습에 포함되지만, 보통 딥러닝과 딥러닝이 아닌 머신러닝을 머신러닝으로 구분하여 표현한다.)은, 사람이 얼마나 개입을 하느냐 이다.

머신러닝 에서는 이미지에서 feature을 추출하여 벡터로 변환하고, 변환된 벡터를 가지고 기계가 자동으로 학습한다. 하지만, 이러한 feature 추출부터 벡터화 까지는 인간이 담당해야 한다.
반면, 딥러닝 의 신경망은 이미지를 '있는 그대로' 학습하여 feature도 기계가 스스로 학습하여 'end-to-end machine learning' 이라고도 표현한다.

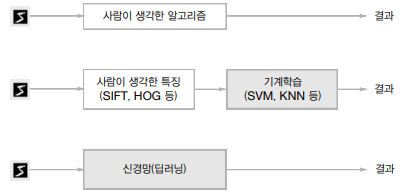
맨 위는 사람이 손글씨 숫자를 분류할 때, 가운데는 머신러닝 기법으로 숫자를 분류할 때, 맨 아래는 딥러닝 기법으로 숫자를 분류할 때의 과정을 간단히 요약한 것이다. 회색 블록은 사람이 개입하지 않음을 뜻한다.

손실 함수

신경망에서는 최적의 매개변수 값 탐색을 위해 손실함수 라는 지표를 사용한다. 이는 현재의 신경망이 훈련 데이터를 얼마나 잘 처리하지 '못'하느냐를 나타내어 클수록 나쁜 성능을 나타낸다.

오차제곱합

Sum of Squares of error 로 줄여서 SSE라고 많이 부른다. 이름 그대로 각 오차들을 제곱하여 더한 값이다.

import numpy as np
	
def sum_squares_error(y, t):
  return 0.5 * np.sum((y-t)**2)

y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

sum_squares_error(np.array(y), np.array(t))

출력 결과

위 코드의 경우는 실제로 정답이 2번 인덱스이고, 예측에서도 2번일 확률이 0.6으로 가장 큰 경우이다. SSE를 계산했더니 위와 같은 값이 나왔다.

y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]

sum_squares_error(np.array(y), np.array(t))

실행 결과

하지만 위처럼 정답일 확률이 0.1로 줄어들면, 그만큼 SSE값은 커짐을 확인할 수 있다.

교차 엔트로피 오차

위 식에서 $t_k$는 정답인 인덱스만 0이다. 따라서, 실질적으로 정답일 때의 추정의 자연로그 $logy_k$를 계산하는 식이 된다($k$번째 인덱스가 정답일 경우)

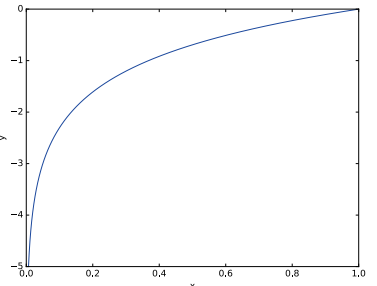
위는 자연로그 $y = logx$의 그래프이다. x값(위에서 $y_k$)이 1에 가까울 수록 0에 가까운 값을 가진다. 즉, 정답 인덱스의 출력 확률이 높을 수록 작은 값을 가진다.

def cross_entropy_error(y, t):
  delta = 1e-7
  return -np.sum(t * np.log(y + delta))
  
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
cross_entropy_error(np.array(y), np.array(t))

y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
cross_entropy_error(np.array(y), np.array(t))

방금 전 실습과 마찬가지로 위는 정답 예측 확률이 높은 경우, 아래는 낮은 경우의 교차 엔트로피 오차 값이다. 정답 확률이 높은 경우가 더 작은 값을 갖는 것을 확인할 수 있다.

미니배치 학습

위에서 살펴본 경우는 하나의 데이터에 대한 손실 함수이다. 따라서 $N$개의 데이터를 훈련데이터로 입력하였을 경우의 교차 엔트로피 오차는 아래와 같다.

단순히 위의 교차 엔트로피 오차 식을 $N$개로 확장한 것이지만, 추가적으로 $1/N$로 나누어 정규화하여 '평균 손실 함수'를 구한다. 따라서 훈련 데이터가 1000개든 10000개든 통일된 지표를 얻을 수 있다.

하지만, 훈련 데이터가 많아진다면 손실함수 합을 구하는 시간이 오래 걸리게 된다. 그래서 미니배치 학습 기법을 이용한다. 예를 들면 지난 포스팅에서 살펴봤던 MNIST 데이터 셋의 60000장의 훈련 데이터 중 100장만을 무작위로 뽑아 학습하는 것이다.

import sys, os
sys.path.append('/content/drive/MyDrive/dnn_study')
import numpy as np
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = \
  load_mnist(normalize=True, one_hot_label=True)

print(x_train.shape)
print(t_train.shape)

출력 결과

train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]

다음과 같이 np.random.choice() 함수를 이용하여 랜덤으로 원하는 개수만큼 뽑아낼 수 있다. 예시에서는 전체 0부터 59999까지의 인덱스 중 10개의 인덱스를 랜덤으로 뽑고 있다.

(배치용) 교차 엔트로피 오차 구현

def cross_entropy_error(y, t):
  if y.ndim == 1:
    t = t.reshape(1, t.size)
    y = y.reshape(1, y.size)

  batch_size = y.shape[0]
  return -np.sum(t * np.log(y + 1e-7)) / batch_size

$y$가 1차원 데이터라면, reshape 함수로 데이터의 형상을 바꿔주고, 배치 크기로 나눠 정규화하고 이미지 1장 당 평균의 교차 엔트로피 오차를 계산한다.

만약, 정답 레이블이 원-핫 인코딩이 아닌, '2'나 '7'등의 숫자 레이블로 주어진 경우의 교차 엔트로피는 아래와 같이 구현 가능하다.

def cross_entropy_error(y,t):
  if y.ndim == 1:
    t = t.reshape(1, t.size)
    y = y.reshape(1, y.size)

  batch_size = y.shape[0]
  return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

위 구현의 핵심은 t가 0인 원소는 교차 엔트로피 오차도 0이므로 무시해도 좋다는 것이다.

손실함수를 정의하는 이유?

왜 '정확도' 라는 지표를 놔두고 굳이 손실 함수의 값을 이용할까?

신경망 학습에서는 최적의 매개변수를 탐색할 때 손실 함수의 값을 가능한 한 작게 만드는 매개변수 값을 찾는다. 이 때 매개변수의 미분을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복한다.

가중치 매개변수의 손실 함수의 미분이란 '가중치 매개변수의 값을 아주 조금 변화시켰을 때, 손실 함수가 어떻게 변하나' 라는 의미이다. 만약 미분 값이 음수(기울기 음수)이면 매개변수를 양의 방향으로 움직이면 손실 함수가 줄어든다는 의미이다. 아래의 그림을 예로 들어보자.

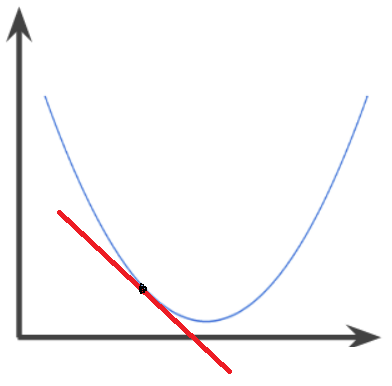
위 그래프를 손실 함수 그래프라고 했을 때, 점이 찍힌 시점에서의 기울기는 음수이다. 이 때 점을 $x$축의 오른쪽(양의 방향)으로 움직이면 손실 함수 값($y$)는 감소한다.

반대로, 미분값이 양수라면 음의 방향으로 움직여야 손실 함수를 줄일 수 있다.

그리고 미분 값이 0이 된다면 어느 쪽으로 움직여도 손실 함수는 줄어들지 않고, 갱신을 멈춘다.

여기서 만약, 손실 함수가 아닌 정확도를 지표로 삼게 된다면 매개변수의 미분이 대부분에서 0이 돼버린다. 만약 100장의 데이터를 입력했을 때 32장을 올바로 인식한다고 하면, 정확도는 32%이다. 여기서, 가중치를 조금만 바꾼다면 정확도는 그대로 32%일 것이고, 일정 변화량을 넘기면 정확도는 31%나, 33%로 훅 뛸 것이다. 가중치를 미세하게 조정한 결과 100장 중 32장 맞히던 걸 32.1231..장을 맞힌다고 할 순 없다. 때문에 미세한 가중치 변화로 인한 성능 변화를 충분히 설명할 수 없다.

이러한 이유로 미세한 가중치 변화에 맞추어 변화량을 디테일하게 알려주는 손실 함수를 이용하는 것이다.

수치 미분

미분

미분은 한 순간의 변화량을 표시한 것이다.

좌변은 $f(x)$의 $x$에 대한 미분을 나타낸다. 이는 $x$의 작은 변화가 함수 $f(x)$를 얼마나 변화시키느냐를 의미한다. $h$는 시간의 작은 변화로, 0에 한없이 가깝게 하여 그만큼 아주 작은 변화량을 의미한다.

def numerical_diff(f, x):
  h = 1e-4 # 0.0001
  return (f(x+h) - f(x-h)) / (2*h)

미분 함수는 다음과 같이 구현 가능하다. 이 때, h를 $1e-50$ 같은 너무 작은 수로 설정하여 소수점 8자리 이하가 되면 반올림 오차로 인해 파이썬은 이를 $0.0$으로 인식하여 문제가 발생하기 때문에 적절히 작은 값인 $1e-4$로 설정해 주었다.

사실, 이렇게 $h$를 무한히 0으로 좁히는 것은 불가능하기 때문에, 엄밀히 따지자면 수치 미분에는 오차가 존재한다.

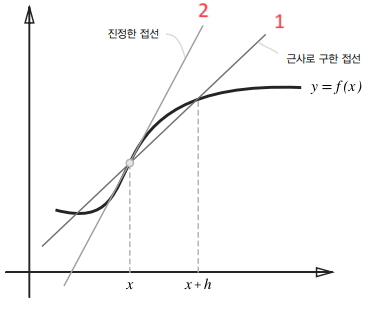
위 그림처럼 실제 접선은 2번이지만, 우리가 근사로 구한 접선은 1번이다.
이러한 오차를 줄이기 위해 $(x+h)$와 $(x-h)$일때의 함수 $f$의 차분을 구하는 중심 차분 방법을 쓰기도 한다. 아래와 같이 구현 가능하다.

def numerical_diff(f, x):
  h = 1e-4 # 0.0001
  return (f(x+h) - f(x-h)) / (2*h)

수치 미분 예시

이차 함수 $y = 0.01x^2 + 0.1x$ 의 그래프를 그려보자.

def function_1(x):
  return 0.01*x**2 + 0.1*x

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x,y)
plt.show()

출력 결과

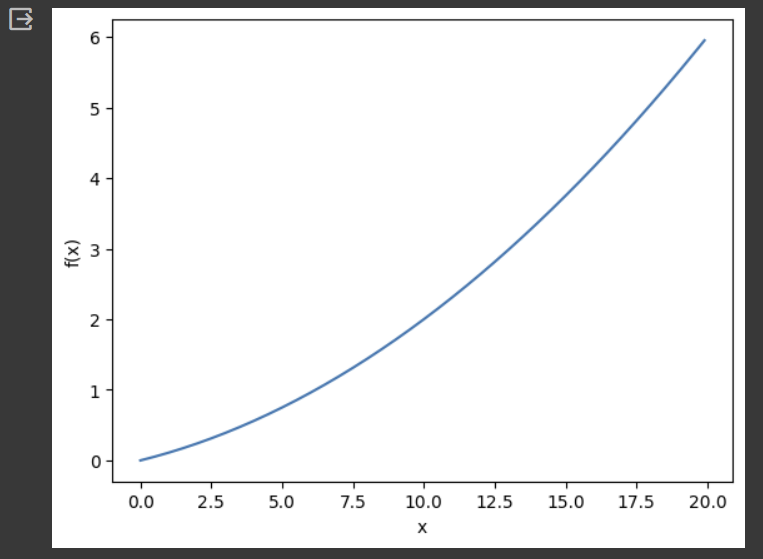
위 그래프에서 $x=5, x=10$일 때의 기울기를 구해보자.

print(numerical_diff(function_1, 5))
print(numerical_diff(function_1, 10))

출력 결과

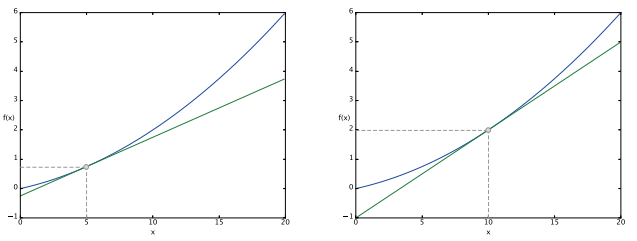
각각 $x=5$에서의 접선과 $x=10$에서의 접선의 기울기가 출력 됨을 확인할 수 있다.

편미분

변수 $x$가 여러개라면 각 변수에 대한 편미분을 계산한다. 아래는 변수 2개인 식이다.

def function_2(x):
  return x[0]**2 + x[1]**2

위 식을 그래프로 그려보면 아래와 같다.

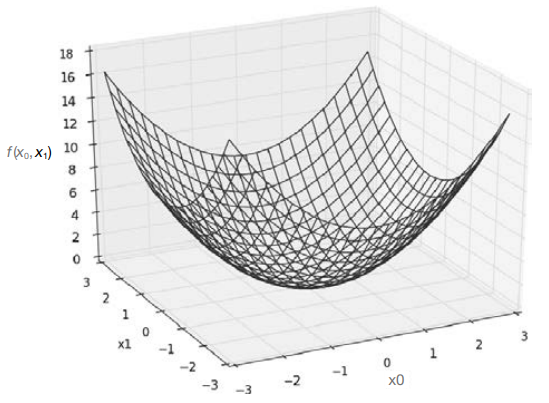
$x_0, x_1$ 각각에 대한 편미분을 구할 수 있고, 수식으로는 $\partial f \over \partial{x_0}$, $\partial f \over \partial{x_1}$, 로 쓴다.

기울기

$x_0, x_1 ... x_n$ 각각의 편미분을 동시에 계산하여 모든 변수의 편미분을 벡터로 정리한 것을 기울기라고 한다. 아래와 같이 구현 가능하다.

def numerical_gradient(f, x):
  h = 1e-4
  grad = np.zeros_like(x)

  for idx in range(x.size):
    tmp_val = x[idx]

    x[idx] = tmp_val + h
    fxh1 = f(x)

    x[idx] = tmp_val - h
    fxh2 = f(x)

    grad[idx] = (fxh1 - fxh2) / (2*h)
    x[idx] = tmp_val

  return grad

numerical_gradient(function_2, np.array([3.0, 4.0]))

실행 결과

파라미터 $x$에는 각 변수들 값이 넘파이 배열로 입력된다. 그 후 for문에서 각 변수의 편미분 값을 구하고 최종적으로 이 값들을 넘파이 배열로 return한다. 예시 코드는 $x_1$이 3, $x_2$가 4인 경우의 $f(x_0, x_1) = x_0^2 + x_1^2$ 에서의 기울기가 된다.

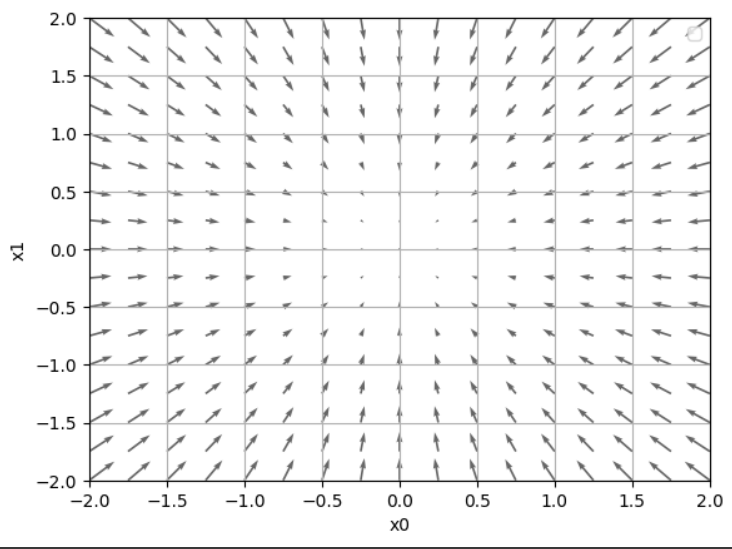
바로 위에 있던 3차원 그림을 위에서 바라본 것이라고 생각해보자. 화살표 길이가 길 수록 경사가 가파르고, 길이가 짧을수록 경사가 완만하다.

경사 하강법

신경망 학습 시 손실 함수를 최소로 만드는 최적 매개변수를 찾는 데 위의 기울기 개념이 매우 중요하게 쓰인다. 경사 하강법은 현 위치에서 기울어진 방향으로 일정 거리만큼 이동하기를 반복하여 함수 값을 점차 줄이는 방법이다. $x$ 변수가 두 개인 함수에서 수식은 아래와 같다.

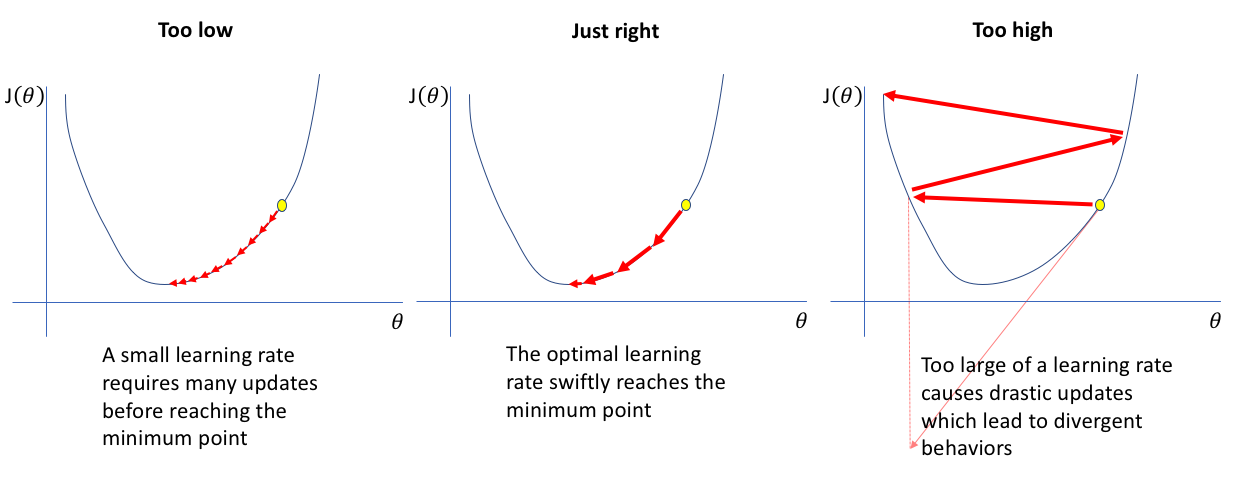
$\eta$는 학습률(learning rate)를 의미하며, 한 번의 학습으로 얼만큼 매개변수를 갱신할 지를 결정한다.

$\eta$값이 너무 작으면 왼쪽 그림처럼 수렴 속도가 너무 느려지고, 반대로 너무 크면 무작위로 튀어 수렴하지 못하게 될 가능성이 크다. 따라서 중앙처럼 적절한 $\eta$ 값을 설정 해주어야 한다.

def gradient_descent(f, init_x, lr=0.01, step_num=100):
  x = init_x

  for i in range(step_num):
    grad = numerical_gradient(f, x)
    x -= lr * grad

  return x

def function_2(x):
  return x[0]**2 + x[1]**2

init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)

출력 결과

위 코드는 간단히 경사 하강법을 구현한 것이다. init_x는 초기 좌표로 $(-3, 4)$, 학습률($\eta$)는 0.01, 얼마나 반복할지의 step_num은 100으로 설정하였다. 그 결과 $(0, 0)$ 에 가까운 결과가 나왔다.

신경망에서의 기울기

신경망 학습에서도 마찬가지로 우리는 기울기를 구한다. 여기서 말하는 기울기는 가중치 매개변수에 대한 손실 함수의 기울기이다. 예를 들어 형상이 2X3, 가중치가 $W$, 손실 함수가 $L$인 신경망의 경우 경사는 $\partial L \over \partial W$ 로 나타낼 수 있고, 수식으로는 아래와 같다.

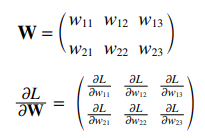
$\partial L \over \partial W$의 각 원소는 각각의 원소에 대한 편미분 값들이다. 간단한 신경망을 예로 들어 실제로 기울기를 구하는 코드를 구현해 보자.

import sys, os
sys.path.append('/content/drive/MyDrive/dnn_study')
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient

class simpleNet:
  def __init__(self):
    self.W = np.random.randn(2,3)

  def predict(self, x):
    return np.dot(x, self.W)

  def loss(self, x, t):
    z = self.predict(x)
    y = softmax(z)
    loss = cross_entropy_error(y, t)
    return loss

simpleNet이라는 클래스를 생성 후, 메서드(함수)를 정의하였다. 여기서 common 파일은 https://github.com/zmfkzj/deeplearning-for-scratch 에서 다운받을 수 있다. 결국 모두 앞에서 구현했던 여러 함수들의 집합체이다.

• predict(self, $x$)

  입력 받은 $x$ 와 가중치를 곱한 결과를 출력해주어 예측을 수행하는 메서드

• loss(self, $x$, $t$)

  predict의 결과를 소프트맥스함수로 활성화 후, 정답 레이블과 교차 엔트로피 에러를 계산하여 출력한다.

net = simpleNet()
print(net.W)

실행 결과

가중치 매개변수를 정규분포로 random하게 초기화 한다.

x = np.array([0.6, 0.9])
p = net.predict(x)
print(p)
print(np.argmax(p))

실행 결과

$x$에 0.6, 0.9를 입력하여 결과를 예측하였을 때 각 인덱스를 정답으로 출력할 확률과 이에 따른 정답으로 선택된 인덱스이다.

t = np.array([0, 0, 1])
net.loss(x, t)

출력 결과

실제 정답 레이블로 원-핫 인코딩 된 넘파이 배열과 loss 계산 결과이다.

이제 이 loss 함수 자체를 $f(W)$ 로 설정하여 기울기를 구해보자.

def f(W):
  return net.loss(x, t)
  
dW = numerical_gradient(f, net.W)
print(dW)

각 원소는 각각의 원소에 대한 편미분 값들이다. 예를 들어, $\partial L \over \partial W$의 $\partial L \over \partial w_{11}$ 은 대략 0.07인데, 이는 $w_{11}$을 $h$만큼 늘리면 손실 함수의 값은 0.07$h$ 만큼 증가한다는 것을 의미한다. 따라서 다음 과정에서 $w_{11}$은 음의 방향으로 갱신돼야 할 것이다. 그리고, 갱신되는 양에는 $w_{11}$ 보단 $w_{23}$이 크게 기여한다는 사실도 알 수 있다.

이제 기울기까지 구하는 법을 알았으니 매개변수를 갱신해 보자.

학습 알고리즘 구현

앞서 살펴본 신경망 학습의 절차는 다음과 같다.

1. 미니배치

   훈련 데이터 중 일부를 무작위로 가져온 미니배치의 손실 함수를 줄이는 것을목표로 삼는다.

2. 기울기 산출

   미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구한다. 기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시한다.

3. 매개변수 갱신

   가중치 매개변수를 기울기 방향으로 아주 조금씩 갱신한다.

4. 반복

   1~3 단계를 반복한다.

2층 신경망 클래스 구현

import sys, os
sys.path.append('/content/drive/MyDrive/dnn_study')
from common.functions import *
from common.gradient import numerical_gradient

class TwoLayerNet:
  def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
    # 가중치 초기화
    self.params = {}
    self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
    self.params['b1'] = np.zeros(hidden_size)
    self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
    self.params['b2'] = np.zeros(output_size)

  def predict(self, x):
    W1, W2 = self.params['W1'], self.params['W2']
    b1, b2 = self.params['b1'], self.params['b2']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    y = softmax(a2)
    
    return y

  def loss(self, x, t):
    y = self.predict(x)
    
    return cross_entropy_error(y, t)

  def accuracy(self, x, t):
    y = self.predict(x)
    y = np.argmax(y, axis=1)
    t = np.argmax(t, axis=1)

    accuracy = np.sum(y == t) / float(x.shape[0])
    return accuracy

  def numerical_gradient(self, x, t):
    loss_W = lambda W: self.loss(x, t)

    grads = {}
    grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
    grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
    grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
    grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

    return grads

천천히 메서드와 변수를 정리해보자.

TwoLayerNet 클래스가 사용하는 변수

• params

  신경망의 매개변수를 보관하는 딕셔너리 변수
  params['W1']은 1번째 층의 가중치, params['b1']은 1번째 층의 편향
  params['W2']은 1번째 층의 가중치, params['b2']은 1번째 층의 편향

• grads

  기울기 보관하는 딕셔너리 변수
  grads['W1']은 1번째 층의 가중치의 기울기, grads['b1']은 1번째 층의 편향의 기울기
  grads['W2']은 2번째 층의 가중치의 기울기, grads['b2']은 2번째 층의 편향의 기울기

TwoLayerNet 클래스의 메서드

• __init__(self, input_size, hidden_size, output_size)

  초기화 수행

• predict(self, $x$)

  예측(추론) 수행. 인수 $x$는 이미지 데이터

• loss(self, $x$, $t$)

  손실 함수의 값을 구함.
  인수 $x$는 이미지 데이터, $t$는 정답 레이블

• accuracy(self, $x$, $t$)

  정확도를 구함 (전체 중 몇 장의 이미지를 맞혔는지)

• numerical_gradient(self, $x$, $t$)

  가중치 매개변수의 기울기를 구함

미니배치 학습 구현

신경망 학습으로는 앞에서 설명한 미니배치 학습을 활용한다. 훈련 데이터 중 일부를 무작위로 꺼내고, 그 미니배치에 대해서 경사법으로 매개변수를 갱신하는 방법이다.

import numpy as np
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

train_loss_list = []

iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

for i in range(iters_num):
  # 미니배치 획득
  batch_mask = np.random.choice(train_size, batch_size)
  x_batch = x_train[batch_mask]
  t_batch = t_train[batch_mask]

  # 기울기 계산
  grad = network.numerical_gradient(x_batch, t_batch)

  # 매개변수 갱신
  for key in ('W1', 'b1', 'W2', 'b2'):
    network.params[key] -= learning_rate * grad[key]

  # 학습 경과 기록
  loss = network.loss(x_batch, t_batch)
  train_loss_list.append(loss)

위 코드에서는 미니배치 크기를 100으로, iters_num(반복 횟수)를 10000로 설정했다. 즉, 60000장의 훈련 데이터에서 임의로 100장의 데이터를 추려내고, SGD(확률적 경사 하강법)을 수행하여 매개변수를 갱신하는 과정을 10000번 수행한다.

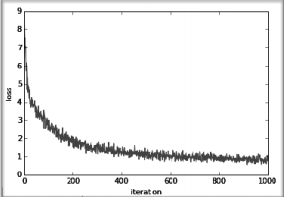
아래는 위와 같이 10000번 반복의 SGD를 수행한 결과 loss값 변화 추이이다.

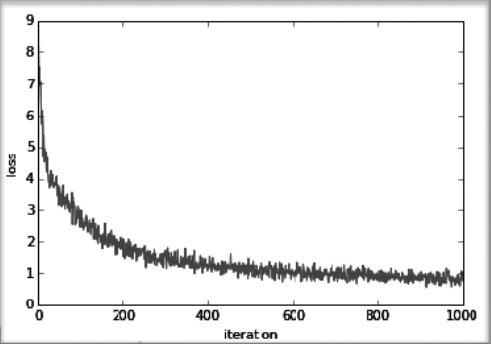
시험 데이터로 평가하기

위 그래프와 같이 훈련 데이터의 손실 함수 값이 줄어들어 신경망 학습이 잘 이루어지고 있다고 할 수 있지만, 한가지 추가로 생각해야할 점이 있다. 바로 우리의 학습 모델이 다른 데이터셋에서도 비슷한 결과를 내는지 이다.

신경망 학습에서 훈련 데이터에서만 좋은 성능을 내고 다른 데이터 셋에서는 낮은 성능을 내는 경우가 있다. 훈련 데이터에 포함된 이미지만 제대로 구분하고, 그렇지 않은 이미지는 식별하지 못하는 것이다. 이를 overfitting(과적합) 이라고 한다.

따라서 훈련 데이터에 포함되지 않은 데이터를 사용하여 평가하는 과정을 걸쳐야 한다. 아래 구현 코드에서는 학습 도중 주기적으로 훈련 데이터와 시험 데이터를 대상으로 정확도를 기록한다.

import numpy as np
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

# 하이퍼 파라미터
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
  # 미니배치 획득
  batch_mask = np.random.choice(train_size, batch_size)
  x_batch = x_train[batch_mask]
  t_batch = t_train[batch_mask]

  # 기울기 계산
  grad = network.numerical_gradient(x_batch, t_batch)

  # 매개변수 갱신
  for key in ('W1', 'b1', 'W2', 'b2'):
    network.params[key] -= learning_rate * grad[key]

  # 학습 경과 기록
  loss = network.loss(x_batch, t_batch)
  train_loss_list.append(loss)

  # 1에폭 당 정확도 계산
  if i % iter_per_epoch == 0:
    train_acc = network.accuracy(x_train, t_train)
    test_acc = network.accuracy(x_test, t_test)
    train_acc_list.append(train_acc)
    test_acc_list.append(test_acc)
    print("train acc, test acc |"
            + str(train_acc) + ", " + str(test_acc))

앞의 코드에서 1 에폭 당 훈련 데이터, 시험 데이터의 정확도를 출력해주는 코드만 추가한 것이다. 여기서 1 에폭(epoch)이란, 학습에서 훈련 데이터를 모두 소진했을 때의 횟수에 해당한다. 예를 들어, 10000개의 훈련데이터를 100개의 미니배치로 학습할 경우 SGD를 100회 반복하면 1 에폭이 된다.

앞의 코드를 실행한 경우 훈련 데이터와 시험 데이터에 대한 정확도 추이를 그려보면 아래와 같이 나온다.

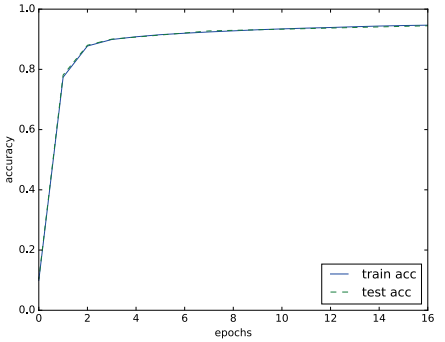
훈련이 진행될 수록 훈련 정확도와 시험 정확도가 유사하게 높아지는 것을 확인할 수 있다. 만약 과적합이 일어났다면, 점선(시험 정확도)이 실선(훈련 정확도)보다 아래에 위치하게 될 것이다.