오차 역전파법

활성화 함수 계층 구현

ReLU 계층

ReLU는 자주 쓰이는 활성화 함수로 수식은 아래와 같다.

$x$에 대한 $y$의 미분은 아래와 같다.

수식은 간단하다. 순전파 때의 입력인 $x$가 0보다 크면 역전파는 상류의 값을 그대로 흘린다. 이러한 역전파의 흐름을 보면 말 그대로 아래 그림과 같다.

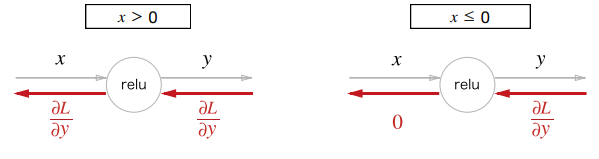
간단하게 ReLU 클래스를 구현해보자.

class Relu:
  def __init__(self):
    self.mask = None

  def forward(self, x): # 순전파
    self.mask = (x <= 0) # mask는 True/False로 구성된 넘파이 배열
    out = x.copy()
    out[self.mask] = 0 # 순전파의 입력인 x의 원소 값이 0 이하인 인덱스는 True, 그 외는 False

    return out

  def backward(self, dout): # 역전파
    dout[self.mask] = 0 # 입력값이 0 이하인 셀만 0으로 변환
    dx = dout

    return dx

import numpy as np

x = np.array([[1.0, -0.5], [-2.0, 3.0]])
x_relu = Relu()
x_relu.forward(x)

출력 결과

Sigmoid 계층

다음은 시그모이드(Sigmoid) 함수 계층이다. 수식은 아래와 같다.

수식을 계산 그래프로 그려보면 아래와 같이 표현할 수 있다.

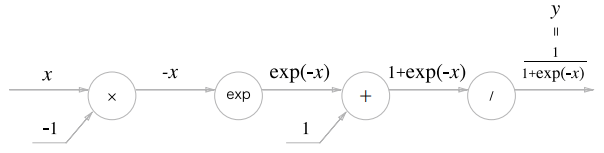
지금까지는 $+$와 $-$ 노드의 역전파 결과만 살펴보았었다. 하지만 그림을 보면 $exp$ 노드와 $/$ 노드가 추가되었는데, 이들은 각각 순전파 때 $y = exp(x)$, $y = {1 \over x}$ 계산을 수행한다.

이제 역전파를 살펴보자.

1. 먼저, $/$ 노드부터 진행해보자. $y = {1 \over x}$ 를 미분하면 아래와 같다.

따라서, 상류에서 들어온 값에 $-y^2$을 곱해서 하류로 흘려보내면 된다.
계산 그래프로 표현하면 아래와 같다.

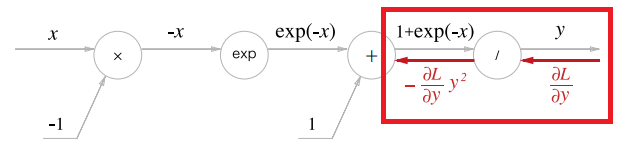
상류에서 흘러들어온 $\partial L \over \partial y$에 $-y^2$을 곱해서 흘러보내는 걸 확인할 수 있다.

2. 다음으로 + 노드는 이전 포스팅에서 다뤘던 그대로, 여과 없이 그대로 하류로 흘려보낸다.

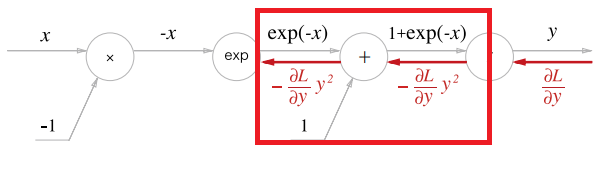
3. $exp(x)$ 연산의 미분은 그대로 $exp(x)$이다. 따라서, 역전파는 순전파 때의 출력을 그대로 하류로 흘려보낸다. 지금같은 경우는 $exp(-x)$를 흘려보내게 되겠다.

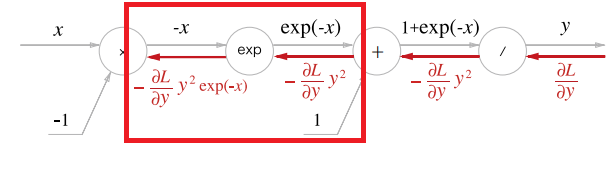
4. 마지막으로, X 노드는 순전파 때의 값을 서로 바꿔 곱하기에, 예시에서는 1을 곱하여 흘려보낸다.
   

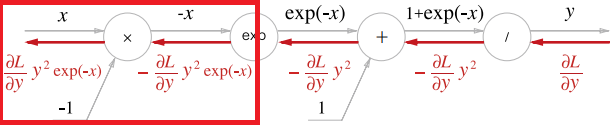
위와 같은 과정을 거쳐 결국 우리는 Sigmoid라는 노드 자체를 만들 수 있다. 상류에서 흘러들어오는 값에 $y^2exp(-x)$를 곱하여 흘려보내는 것과 같다.

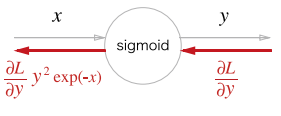
위에서 정리한 ${\partial L \over \partial y} y^2exp(-x) 를$ 더 간단하게 출력($y$)만으로도 표현이 가능하다.

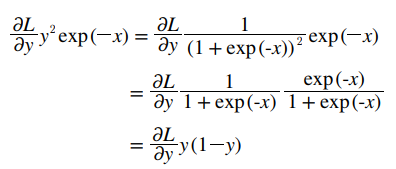
이러한 점을 이용하여, 시그모이드 클래스를 구현해보자.

class Sigmoid:
  def __init__(self):
    self.out = None

  def forward(self, x):
    out = 1 / (1 + np.exp(-x))
    self.otut = out

    return out

  def backward(self, dout):
    dx = dout * (1.0 - self.out) * self.out

    return dx

Affine 계층

신경망의 순전파 때 수행하는 행렬의 곱을 어파인(Affine) 변환 이라고 한다. 지금까지의 계산 그래프는 노드 사이에 '스칼라 값'이 흘렀는 데, 이에 반해 '행렬'이 흐르고 있다고 생각하자.

$X$와 $W$의 행렬 곱을 미분하여 역전파 관점에서 보았을 때, 각 식은 다음과 같다.

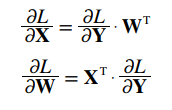
$Y = X \cdot W + B$ 라는 행렬 연산의 역전파 그래프를 그려보자. 여기서 $X$는 (1,2), $W$는 (2,3) 형상이다.

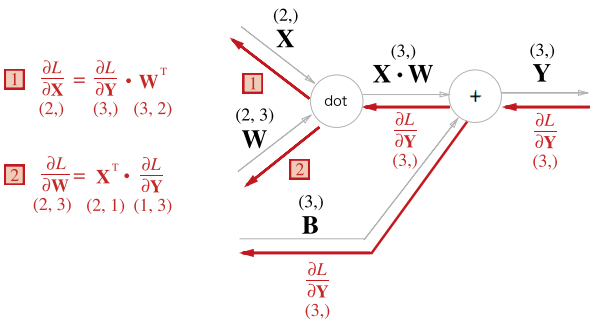
행렬의 곱에서는 대응하는 차원의 원소 수를 맞춰줘야 하기 때문에, 항상 행렬의 형상에 주의하여야 한다.

배치용 Affine 계층

위의 Affine변환 경우에는 행렬의 연산이긴 했지만, 모두 행의 형상이 1 (입력 데이터 X가 하나)인 경우를 보았을 때이다. 이번엔 데이터 N개를 묶어서 입력하는 경우의 역전파 계산 그래프를 보자.

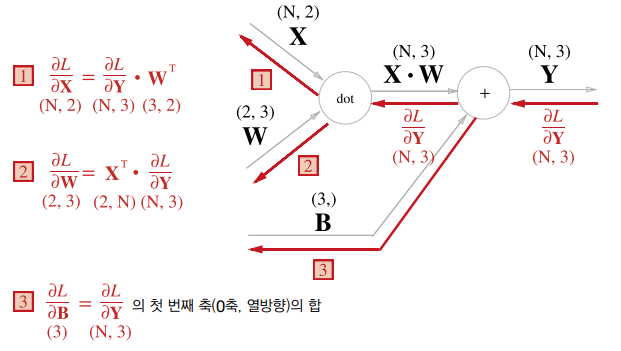
좀 전의 그림에서 행 수만 바뀐 것이다(1 ➤ 3).

이제 Affine 클래스를 구현해보자.

class Affine:
  def __init__(self, W, b):
    self.W = W
    self.b = b
    self.x = None
    self.dW = None
    self.db = None

  def forward(self, x):
    self.x = x
    out = np.dot(x, self.W) + self.b

    return out

  def backward(self, dout):
    dx = np.dot(dout, self.W.T)
    self.dW = np.dot(self.x.T, dout)
    self.db = np.sum(dout, axis=0)

    return dx

여기서 db, 즉 $\partial L \over \partial B$는 순전파의 편향 덧셈이 각각의 데이터에 더해지기 때문에 역전파 때는 편향이 한 원소에 모여야 한다. 형상이 ( , 3) 이므로 같은 행 끼리의 합을 return해 주어야 한다.

Softmax-with-Loss 계층

이전 포스팅에서, 분류 문제의 경우 출력층 활성화함수로 소프트맥스 함수를 쓰는 경우가 많다고 하였다. 이는 각 클래스로 mapping될 확률을 정규화 해주는 역할을 한다.

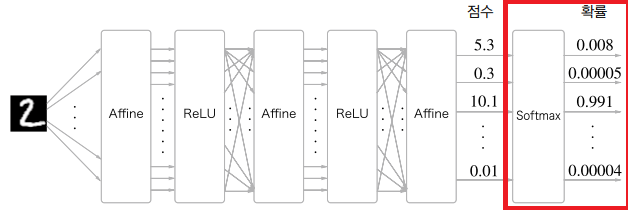
(손글씨 이미지를 입력했을 때 특정 숫자로 mapping될 확률을 보여준다.)

추가로, 우리는 손실함수에 대해서도 정의하였다. 둘을 연결지은 Softmax-with-Loss 계층을 간소화하여 살펴보자.

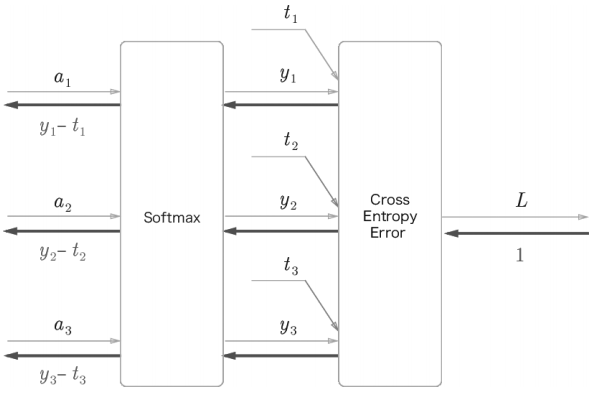
자세한 계산 과정은 생략했지만, 결과만 보면 소프트맥스 계층의 역전파 결과는 $(y_1 - t_1, y_2 - t_2, y_3 - t_3)$이다. 이 때 $(y_1, y_2, y_3)$는 정규화(소프트맥스) 된 각 클래스로 mapping될 확률이고, $(t_1, t_2, t_3)$는 각 정답 레이블 값이다. 역전파 결과가 꽤 간단한데, 이는 손실함수인 '교차 엔트로피 오차'가 그렇게 설계되었기 때문이라고 한다.

아래는 구현 코드이다.

class SoftmaxWithLoss:
  def __init__(self):
    self.loss = None
    self.y = None
    self.t = None

  def forward(self, x, t):
    self.t = t
    self.y = softmax(x)
    self.loss = cross_entropy_error(self.y, self.t)
    return self.loss

  def backward(self, dout=1):
    batch_size = self.t.shape[0]
    dx = (self.y - self.t) / batch_size
    return dx

오차 역전파법 구현

오차 역전파법을 적용한 신경망 구현

지난 포스팅, 4장에서는 수치 미분을 이용하여 기울기를 구하였다. 이번에는 그 대신 오차 역전파법(해석적 방법)을 통해 훨씬 빠르게 기울기를 구할 수 있다.

이제 2층 신경망의 오차 역전파법을 구현해보자. TwoLayerNet이라는 클래스로 정의한다. common 파일은 https://github.com/youbeebee/deeplearning_from_scratch 에서 받을 수 있다.

from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict

class TwoLayerNet:
  def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):

    # 가중치 초기화
    self.params = {}

    self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
    self.params['b1'] = np.zeros(hidden_size)

    self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
    self.params['b2'] = np.zeros(output_size)

    # 계층 생성
    self.layers = OrderedDict()
    self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
    self.layers['Relu1'] = Relu()
    self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
    self.lastLayer = SoftmaxWithLoss()

  def predict(self, x):
    for layer in self.layers.values():
      x = layer.forward(x)

    return x

  # x : 입력 데이터, t : 정답 레이블
  def loss(self, x, t):
    y = self.predict(x)
    return self.lastLayer.forward(y, t)

  def accuracy(self, x, t):
    y = self.predict(x)
    y = np.argmax(y, axis=1)
    if t.ndim != 1:
      t = np.argmax(t, axis=1)

    accuracy = np.sum(y==t) / float(x.shape[0])
    return accuracy

  # x : 입력 데이터, t : 정답 레이블
  def numerical_gradient(self, x, t):
    loss_W = lambda W: self.loss(x, t)

    grads = {}
    grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
    grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
    grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
    grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
    return grads

  def gradient(self, x, t):
    # 순전파
    self.loss(x, t)

    # 역전파
    dout = 1
    dout = self.lastLayer.backward(dout)

    layers = list(self.layers.values())
    layers.reverse()
    for layer in layers:
      dout = layer.backward(dout)

    # 결과 저장
    grads = {}
    grads['W1'] = self.layers['Affine1'].dW
    grads['b1'] = self.layers['Affine1'].db
    grads['W2'] = self.layers['Affine2'].dW
    grads['b2'] = self.layers['Affine2'].db
    return grads

TwoLayerNet 클래스의 인스턴스 변수와 역할을 정리하면 아래와 같다.

• params

  딕셔너리 변수로, 신경망의 매개변수를 보관

• layers

  순서가 있는 딕셔너리 변수로, 신경망의 계층을 보관

• lastLayer

  신경망의 마지막 계층. 위 같은 경우는 SoftmaxWithLoss

다음은 TwoLayerNet 클래스의 메서드 정리이다.

• __init__(self, input_size, hidden_size, output_size, weight_init_std)

  초기화를 진행하며 인수는 앞에서부터 (입력층 뉴런 수, 은닉층 뉴런 수, 출력층 뉴런 수, 가중치 초기화 시 정규분포의 스케일)을 의미한다.

• predict(self, x)

  예측을 진행한다. 현재 예제에서 x는 이미지 데이터이다.

• loss(self, x, t)

  손실 함수의 값을 구한다. 인수 x는 이미지 데이터, t는 정답 레이블

• accuracy(self, x, t)

  정확도를 구한다.

• numerical_gradient(self, x, t)

  가중치 매개변수의 기울기를 수치 미분 방식으로 구한다.

• gradient(self, x, t)

  가중치 매개변수의 기울기를 오차역전파법으로 구한다.

오차 역전파법을 사용한 학습 구현

이제 위에서 정의한 TwoLayerNet을 이용하여 학습 모델링을 구현해보자.

import sys, os
sys.path.append('/content/drive/MyDrive/dnn_study')
import numpy as np
from dataset.mnist import load_mnist

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
  batch_mask = np.random.choice(train_size, batch_size)
  x_batch = x_train[batch_mask]
  t_batch = t_train[batch_mask]

  # 오차역전파법으로 기울기를 구한다.
  grad = network.gradient(x_batch, t_batch)

  # 갱신
  for key in ('W1', 'b1', 'W2', 'b2'):
    network.params[key] -= learning_rate * grad[key]

  loss = network.loss(x_batch, t_batch)
  train_loss_list.append(loss)

  if i % iter_per_epoch == 0: # 600 단위마다 정확도 출력
    train_acc = network.accuracy(x_train, t_train)
    test_acc = network.accuracy(x_test, t_test)
    train_acc_list.append(train_acc)
    test_acc_list.append(test_acc)
    print(train_acc, test_acc)

출력 결과

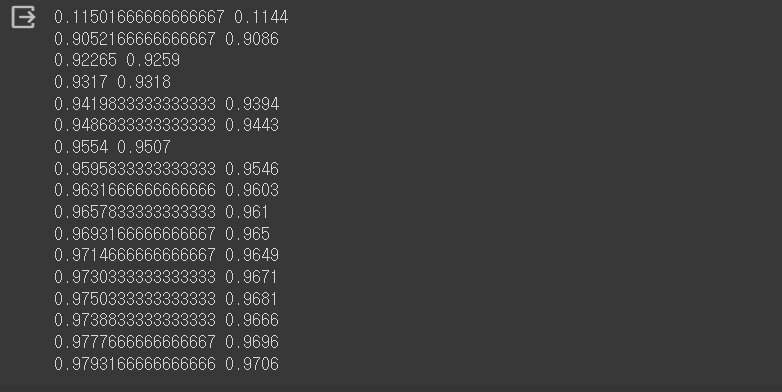
총 6만 장의 데이터를 배치 사이즈 100으로 나눠 iter_per_epoch을 600으로 설정하였기 때문에, 600 단위마다 train, test 정확도를 출력한다. 최종적으로 0.97의 정확도를 보여주고 있다.