3차원인 슈뢰딩거 방정식은 손으로 풀기에 복잡하다.
몇 가지 가정을 고려해서 간략하게 만들도록 한다.
1차원 슈뢰딩거 방정식

위치에너지가 시간에 무관하다고 가정하고 문제를 풀어보자.
파동함수 프사이는 위치와 시간을 분리한다.
좌변은 위치에 대한 미분방정식 우측은 시간에 대한 미분방정식 으로 나눈다.
시간에 대한 1차원 미분방정식

오일러공식을 이용해서 파동을 복소수로 나타낸다.
관계식을 이용해 에타는 에너지의 값을 뜻한다.
위치에 대한 1차원 미분방정식

k가 해를 결정짓는다.

전 범위에서의 확률밀도함수는 1이 되어야한다.
자유전자의 운동량
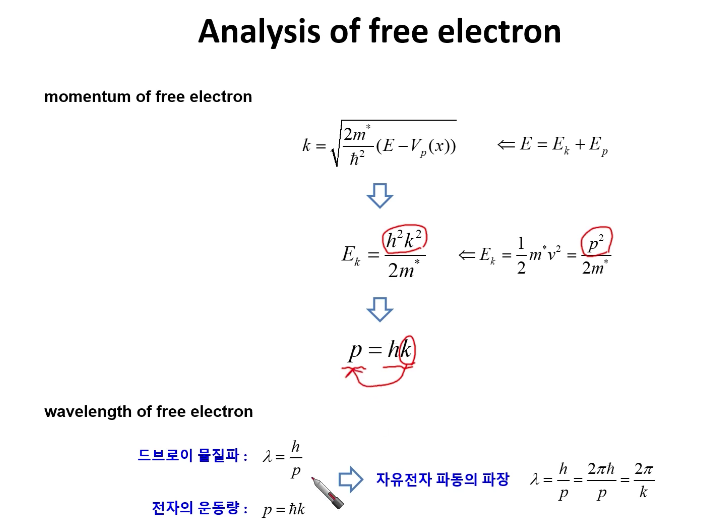
자유전자 파동의 파장 ㅅ 은 2파이/k이다.
자유전자의 위치

전자가 존재할 확률이 상수로 나왔다. - 모든 위치에서 발견될 확률이 동일하다. - 모든곳에 전자가 존재한다.
전자의 에너지가 결정되면, 전자의 운동량도 결정된다.
모든 곳에 전자가 존재한다면 위치를 알 수 없다.
이게 하이젠버그의 불확정성 원리이다.
요약
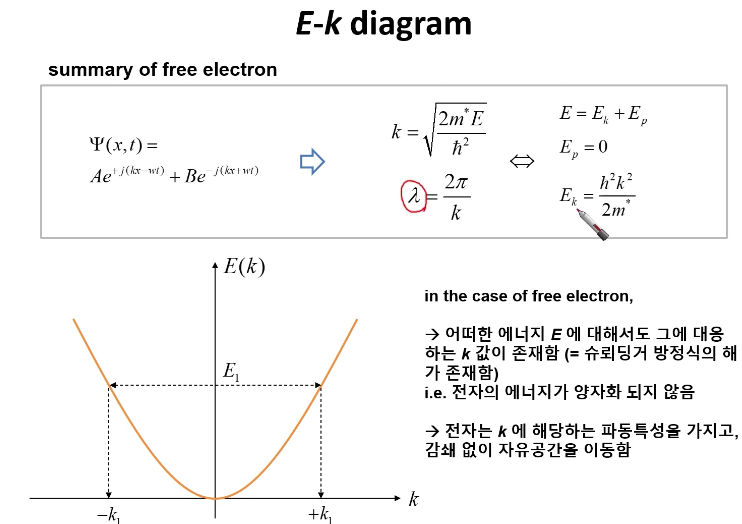
파동함수가 결정되고 전파상수 k를 구하게 되면
전자의 파동의 파장, 운동에너지를 구할 수 있다.
k값이 전자의 파동을 결정하는데 중요하기 때문에 에너지와 어떻게 연결되는지
알기 위해 E-k 그래프를 그린다.
2개의 댓글
안녕하세요 글 잘 보고 있어요..!
제가 요즘 많이 고심하는데도 모르겠어서
여쭤보고 싶은 공업수학 문제가 있는데
혹시 답변 해주실 수 있으실까요..?
곤란 하시다면 답변 안 해주셔도 괜찮아요
문제는 이거예요…!
“분리가능 상미분 방정식은 양형태 상미분 방정식의 일부이고, 완전 상미분 방정식은 음형태 상미분 방정식 일부라고 볼 수 있다.
양형태의 상미분 방정식 중 분리가능한 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 분리가능하지 않은 상미분 방정식들), 음형태의 상미분 방정식 중 완전 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 완전하지 않은 상미분 방정식들) 쓰시오.
즉.
양형태의 상미분 방정식의 전체 집합을 W.
음형태의 상미분 방정식의 전체 집합을 U,
분리가능한 상미분 방정식의 전체 집합을 A,
완전 상미분 방정식의 전체 집합을 B
라고 할 때
집합 A^c ᑎ W 과 집합 B^c ᑎ U 에 대해 기술하는 문제이다. 그 집합에 해당하는 미분 방 정식의 예를 몇 개 구하고 그들의 공통된 특징을 기술하는 방법을 써도 좋고, 아니면 이 집 합에 속하는 방정식들의 특징을 바로 기술하여도 좋다.“





안녕하세요 좋은 글 감사합니다. 질문이 있는데요, 1차원 슈뢰딩거 해에서 왜 2가지 형태로 나오는지궁금합니다. 각각 성립이 된다는것은 이해했는데, 보통 particle in a box에서는 Acos(kx)+ Bsin(kx) 형식으로 쓰더라구요,(저희 교수님께서는 Aexp(jkx)+Bexp(-jkx) 를 이용하셨습니다. ) 혹시 어떤차이인지 알수있을까요?