백준 20293번 - 연료가 부족해 [파이썬/Python]

문제

https://www.acmicpc.net/problem/20293

풀이

$Dynamic Programing + Binary$_$search$

출발점에서 연료량을 x라고 할 때, 피라미드까지 도달 가능한지 판단한다.

1. 자동차가 오른쪽과 아래로만 이동할 수 있으므로, 연료 보관소들을 (r + c)가 작은 순서로
   오름차순 정렬

2. $dp[i]$를 $i$번째 연료 보관소에 도착해서 보관된 연료를 충전했을 때, 현재 남은 자동차
   연료량으로 정의할 때, 점화식을 도출한다.
   

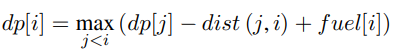
3. $dp[j] \geq dist(j, i)$의 조건을 만족해야한다. $j$ 연료보관소에서 $i$연료 보관소로 이동할 때, 이동할 거리보다 연료의 양이 적다면 이동을 못하기 때문이다.

4. $1$ ~ $N$연료 보관소를 순서대로 방문하면서 $dp$를 갱신했을 때,
   피라미드에 도달하지 못한다면 더 많은 연료를 충전하고
   피라미드에 도달할 수 있다면 더 적은 연료로 피라미드에 도착할 수 있는지 확인한다.
   -> 이분탐색을 이용한다.

시간복잡도

✓ $dp$ 배열 탐색 시 $O(N^2)$,

✓ 연료보관소를 $(r+c)$ 순서로 정렬할 때 $O(NlogN)$,

✓ $x$에 대해 이분탐색을 진행할 때, x는 $2$ ~ $(R+C-2)$의 범위를 가지므로 $O(log(R+C-2))$

∴ $O(N^2log(R+C-2))$의 시간 복잡도를 가진다.
최대 $10^6 * log(5998) \approx 12,550,265$로 시간제한 1초(100,000,000)를 만족한다.

코드

import sys
input = sys.stdin.readline

R, C = map(int, input().split())
n = int(input())

# 연료
fuel = []
for _ in range(n):
    fuel.append(list(map(int, input().split())))

# 시작점, 도착점 추가
fuel.append([1,1,0])
fuel.append([R,C,0])

# 0,0부터 좌표까지의 맨해튼거리로 정렬
fuel.sort(key = lambda x:x[0] + x[1])

# 두 좌표간의 거리
def dist(i, j):
    return (fuel[i][0]-fuel[j][0])+ (fuel[i][1]-fuel[j][1])

def find(x):
    global R, C, n
    #연료 충전소에 도착해서 충전 시 "얼마만큼의 연료를 가지고 있는지"
    dp = [-1] * (n+2)

    # 시작점의 연료를 x만큼 채우고 출발한다.
    dp[0] = x
    fuel[0][2] = x

    for i in range(1,n+2):
        for j in range(i):
            # i번째 노드가 j번쨰 노드보다 오른쪽, 아래에 위치해야 한다.
            if fuel[j][0] > fuel[i][0] or fuel[j][1] > fuel[i][1]:
                continue

            # 이전 노드의 연료만으로 다음 노드로 도착할 수 있는가?
            if dp[j] < dist(i, j):
                continue
            
            #항상 큰 값으로 연료를 갱신해준다.
            dp[i]=max(dp[i], dp[j] - dist(i, j) + fuel[i][2])

    if dp[-1] >= 0:
        return True
    else:
        return False


# 처음에 충전하는 연료의 양을 기준으로 이분탐색
start = 1
end = R+C-2

while start <= end:
    mid = (start + end) // 2

    if find(mid):
        end = mid - 1

    else:
        start = mid + 1

print(start)

Note:

처음에 모든 경우의 수를 따져봐야 한다는 생각에 dfs를 생각해봤지만 도저히 풀리지 않아서 어려웠던 문제였다.

온전히 내 생각으로는 풀지 못했고, $dp$를 이용해야한다는 힌트를 얻고나서 고민끝에 문제를 해결할 수 있었다.

$dp$와 이분탐색을 이용해 문제를 해결해야하는 새로운 접근법을 가진 재밌는 문제였다.

알고리즘 문제풀이 코드를 Github에 업로드하고 있습니다.

링크 : https://github.com/bbamjoong/Algorithm.git