[BOJ] 백준 11444 피보나치 수 6 python

Jihan·2024년 5월 5일

python 거듭제곱 백준 선형대수학 알고리즘 문제 피보나치 행렬

알고리즘

목록 보기

4/6

백준 Online Judge 문제

11444번: 피보나치 수 6

풀이과정

오늘 풀어볼 문제는 solved.ac의 클래스4 문제로, 나한테는 남아있는 마지막 클래스4++ 문제인 11444번 피보나치 수 6이다. 다른 피보나치 시리즈를 모두 풀어보지는 않았지만, 역시 수학문제답게 문제 입력 출력이 아주 짧고 명료하다.

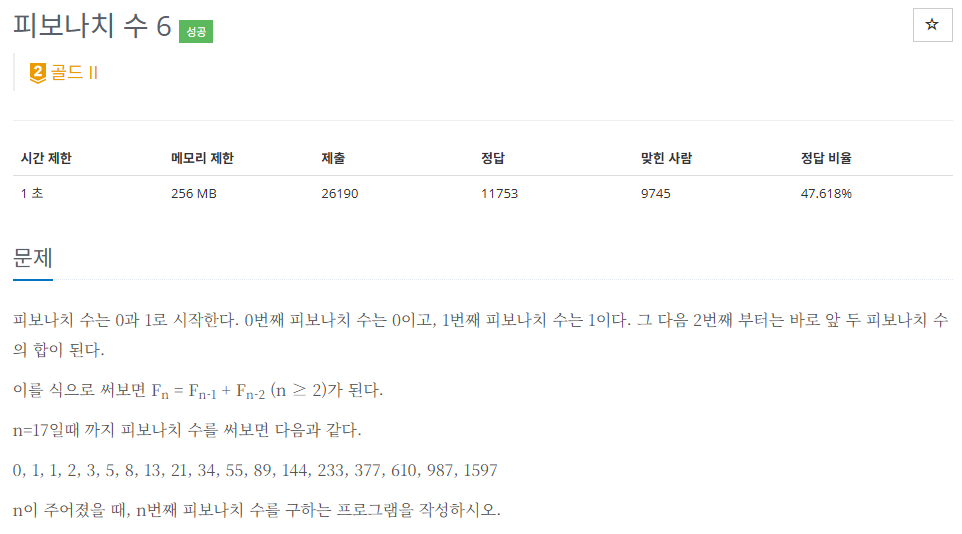
문제
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다.

이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다.

n=17일때 까지 피보나치 수를 써보면 다음과 같다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597

n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.

입력
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.

출력
첫째 줄에 n번째 피보나치 수를 1,000,000,007으로 나눈 나머지를 출력한다.

마지막으로 풀어본 피보나치 문제는 완전 코린이 시절 점화식을 재귀 함수로 표현하는 재귀 함수형 구현과, 이 때 발생하는 콜 스택 메모리에 대한 문제와 입력이 여러 개일 경우를 대비할 수 있는 Memoization을 활용한 DP형 구현이었다.

근데 얼핏 보아하니, 시간 제한은 1초이다. 이러한 풀이로 풀기에는 시간이 너무 부족하다...! 애초에 입력의 자릿수를 보아하니, 이렇게 일반적인 점화식으로 풀 수 있는 문제가 아니다.

반대로 생각해봤을 때, 입력의 자릿수가 저렇게 크면 절대로 O(N)으로 풀이할 수 없다. 당연히 O(logN)으로 풀어내야겠다고 생각이 들어야 한다.

일단 시간 복잡도를 낮출 수 있는 여러 가지 방법들을 떠올려보았다.

첫 번째, 피보나치 수열이 특정 큰 값들에 대해서(% 1,000,000,007) 일정한 주기를 가지고 반복되는가?

그렇다고 하더라도, 문제 자체에서 주어지는 저 큰 값은 모듈러 연산을 위해 백준에서 주어주는 상당히 큰 소수에 불과하다. int overflow를 막기 위한 값으로 주는 것이라고 보면 된다. 따라서 이런 식의 풀이는 가능하다 하더라도 꼼수에 가깝다고 느껴진다.

그래도 풀리기만 하면 장땡이라는 생각에 반복해보았다. 처음으로 주어진 나머지 연산을 위한 큰 값보다 커지는 행은 n=46일 때이다. 확률적으로 같은 값이 나오려면 저 큰 값 만큼의 반복이 이루어져야 하고, n=10000000053쯤 되면 다시 n=46일 때의 값이 반복될 기대가 충족된다. 하지만 피보나치 수열은 단순이 n-1행의 값뿐만이 아니라 그 전의 값에도 영향을 받기 때문에, 최소 10억회 이상의 덧셈 연산이 필요하다. 또한 이 모든 값을 저장해두지 않으면 의미가 없어지는 형태이기 때문에, 이 방법은 틀렸다.

위의 풀이에 대해 생각해보다가, 일반적이지 않은 트리키한 시간복잡도 낮추기는 의미가 없는 문제라는 생각이 들었다. O(N)의 덧셈에 대한 시간복잡도를 O(logN)으로 낮춘다는 것은, 나의 미천한 수학적 직감으로 'N이 엄청 크니까, 이걸 반으로 쪼개는 걸 반복하는 분할 정복 형태로 풀 수는 없을까?'하는 생각으로 이어졌다.

두 번째, 분할 정복으로는 풀 수 없을까?

분할 정복으로 문제를 풀어내기 위해서는 분할할 기준을 만들어야 한다. 나에게 주어진 이 문제에서의 점화식은
Fn = Fn-1 + Fn-2 (n ≥ 2)
이게 전부이다. 이런 생각을 해보았다. 특정 항 번호를 가지고 오면 충분히 크지만 연산이 가능한 여러 항들의 합으로 분해해서 표현하고, 이렇게 되면 어느 정도까지 곱셈으로 변환하여 풀 수 있지 않을까?

머릿 속으로 대충 계산을 해보았다.
n=6일 때, F6 = F4 + F5
F4와 F5는 각각 F2 + F3, F3 + F4이므로
F6 = F2 + 2F3 + F4
다시 쪼개서,
F6 = F0 + 3F1 + 3F2 + F3
= 4F0 + 7F1 + F2
= 5F0 + 8F1
= 8
아주... 효율적으로 비효율적인 풀이인 것 같다. 계속 쪼개다 보면 더 이상 쪼갤 수 없는 F0과 F1로 이루어진 식을 구할 수 있고, 0과 1을 대입하면 값을 구할 수 있게 된다.

지금은 우리가 이미 값을 간단하게 알고 있는 F0과 F1까지 분해하여 대입하였지만, 충분히 뒷 항으로 더 큰 항들을 분해하여 계수 값만을 구하여 곱셈으로 처리할 수는 없을까? 라는 생각이 들었다.

이번에도 일반적이지 못한 풀이였다. 충분히 큰 항에 대한 기준은 어떻게 정할 것이며(코드 상의 n값에 대한 분기), 시간 복잡도를 생각해봤을 때 저 분기 값에 따라 연산의 횟수가 기존보다 줄어드는 수준도 바뀔 것이고, 이는 생각했던 것보다 미미한 차이일 것 같다는 어렴풋한 생각이 들었다.

그래도 여기서 얻은 힌트가 있었다. 내가 식을 쪼개면서, 반복적인 앞의 값에 대한 연산을 앞의 값에 대한 곱셈으로 바꿀 수 있을 거라는 생각이 들었다. 세 번째 풀이는 여기서 이어진다.

세 번째, 덧셈 연산을 곱셈으로 치환할 수는 없을까?: 행렬의 거듭제곱 활용

이 문제를 더하는 문제가 아니라 곱하는 문제로 바꾸면, 지수에 N을 올릴 수 있으니 logN 형태로 바꿀 수 있지 않을까?라는 생각이 들었다.

특정 계수를 피연산자로 하는 곱셈이라면 좋지만, 거듭제곱의 형태라면 더더욱 좋을 것이다.

여기서 혼자 떠올리는 부분에 한계가 왔다. 분명 계수에 대한 곱셈이나 거듭제곱 형태로 피보나치 수열을 표현할 수 있다면, 이건 피보나치 수열의 일반항을 구하는 것이 될 텐데 이렇게 유명한 이야기를 내가 모르고 있을까?하는 의문점이 생겼다.

그래서 살짝 화가 난 상태로 검색해보았는데...
행렬을 이용하여 피보나치 수열의 일반항을 구하는 방법이 있었다. 충격적이다... 내 수학에 대한 무지는 어느 정도인가 싶은 회의가 있었지만 그래도 꾹 참고 문제를 이어서 풀어보자. 이 일반항까지 가져다가 사용하지는 않아도 될 것 같다.

그래도 알아낸 정보에 대해 간단하게 정리하자면, 피보나치 수열의 점화식을 행렬의 곱셈 식으로 다음과 같이 표현할 수 있다.

{{a_{n+1}} \choose {a_{n}}} = {\begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix}}^n{1 \choose 0}

나무위키에서는 아래와 같은 형태로 표현하는 것에 대해서도 나와있더라.

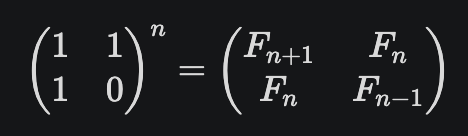
자, 이 두 식을 활용함과 동시에 우연히 며칠 전에 풀었던 10830번 행렬 제곱 문제에서의 아이디어를 합치면, 우리의 문제를 O(logN)으로 풀어낼 수 있다.
10830번: 행렬 제곱
위 문제에서의 아이디어는 (A^n)(A^m)=A^(n+m)이라는 점을 활용하여 거듭 제곱에 분할 정복 형태를 적용하면서 시작된다. 일반적으로 아래의 식으로 전체 연산을 분할하여 푸는 것으로 알려져 있다.

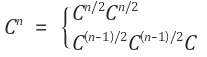
나는 10830 문제는 위의 방식과 살짝 다른 형태로 문제를 풀었었는데, 이 문제에서는 위의 아이디어를 활용해서 코드를 작성해보기로 하였다.

import sys;rl=sys.stdin.readline

mod = 1000000007
matrixC = [[1, 1],[1, 0]]

n = int(rl().strip())
def matrixMul(matA,matB):
  Na, Ma = len(matA), len(matA[0]) # matA = (Na x Ma)
  Nb, Mb = len(matB), len(matB[0]) # matB = (Nb x Mb)
  res = [[0 for _ in range(Mb)] for _ in range(Na)] # matC = (Na x Mb), Ma = Nb
  for i in range(Na):
    for j in range(Mb):
      S = 0
      for k in range(Ma):
        S += matA[i][k] * matB[k][j]
      res[i][j] = S % mod
  return res

def matrixPow(n):
  if n == 1:
    return matrixC
  if n % 2 == 0:
    return matrixMul(matrixPow(n // 2),matrixPow(n // 2))
  else:
    return matrixMul(matrixPow(n - 1), matrixC)

print(matrixPow(n)[0][1])

두구두구... TLE가 나왔다. 앞의 몇 개는 풀렸는데, 중간에 시간 초과가 나왔다. 행렬의 곱을 활용하면 단순 항의 거듭제곱을 구하는 것보다 훨씬 많은 양의 연산을 요구하기 때문에 시간초과가 나는 것 같다. 곱셈 연산이 유동적인 크기의 행렬에 대해서도 가능하도록 구현한 것이 문제일 수도 있다고 생각했고, 2x2행렬에 대해서만 작동하도록 구현해보았다. 마찬가지로 TLE.

자, 구현 방식을 바꿔보자.
아무래도 메모이제이션을 활용하지 못해서 그런 것 같다는 생각이 들었고, 내가 기존에 10830번 문제(행렬 제곱)를 풀었을 때의 구현 방식을 떠올려보았다.

나는 지수를 계속해서 2로 나누면서 분할하는 것이 아니라, 지수값보다 작으면서 가장 큰 2의 거듭제곱 값까지 거듭제곱된 행렬을 미리 구한 뒤, 2의 거듭제곱으로 지수를 쪼갰다(2진수로 표현했다고 생각해도 될 듯).

그 뒤에 각 값들에 대해서 메모이제이션된 값을 가져오고, 곱하는 형태로 구현하였다.

import sys;rl=sys.stdin.readline
import math

mod = 1000000007
matrixC = [[1, 1],[1, 0]]

n = int(rl().strip())
def matrixMul(matA,matB):
  res = [[0 for _ in range(2)] for _ in range(2)]
  for i in range(2):
    for j in range(2):
      S = 0
      for k in range(2):
        S += (matA[i][k] * matB[k][j]) % mod
      res[i][j] = S % mod
  return res

pows = [[[1, 0], [0, 1]], [[1, 1], [1, 0]]]
for _ in range(int(math.log2(n))):
  pows.append(matrixMul(pows[len(pows) - 1], pows[len(pows) - 1]))

def divide(cnt):
  if cnt <= 1:
    return pows[cnt]
  divBigest = int(math.log2(cnt))
  mod = cnt - (2 ** divBigest)
  return matrixMul(pows[divBigest + 1], divide(mod))

print(divide(n)[0][1])

맞았다!
사실 아래의 코드가 코드 상의 시간복잡도는 조금 더 높을 것으로 예상된다. 하지만 메모이제이션을 했다는 부분에서 행렬의 거듭제곱을 계속해서 새로 구하지 않아도 됐기 때문에 TLE가 나지 않고 성공한 것 같다.

회고

오늘 포스팅은 그냥 풀이를 적어내는 것보다는 이런 문제 푸는 사고 과정을 기록해보고 싶었다. 사고 과정 자체를 기록해두기 위해 내가 했던 사고의 과정을 좀 더 논리적으로 정리하려고 하고, 이를 통해서 단순히 직관적으로 생각했던 과정을 구체적으로 만들게 된다면 문제 해결에 어느 정도 도움을 줄 수 있을 거라고 생각한다.

요즘 하루에 한 문제씩 알고리즘 문제를 풀고 있다. 일전에 한창 알고리즘 문제를 풀어냈던 적이 있어서 왠만한 어렵지 않은 문제들에 대해서는 기억을 더듬어가면서 풀어갔는데, 모듈러 연산 관련된 문제들이 몇 개 보이기 시작했고 이 문제들은 확실히 모듈러 연산에 대한 백그라운드가 없으면 못 풀겠구만! 싶었다. 예전에도 모듈러 연산이 알고리즘 문제 풀이에 도움이 될 것 같아서 공부를 좀 했었는데, 역시 실제 프로젝트 등에서 쓰일 일은 거의 없다보니 조금 지나면 까먹고, 조금 지나면 까먹고 한다...