
1. Review
1-1) Activation Function
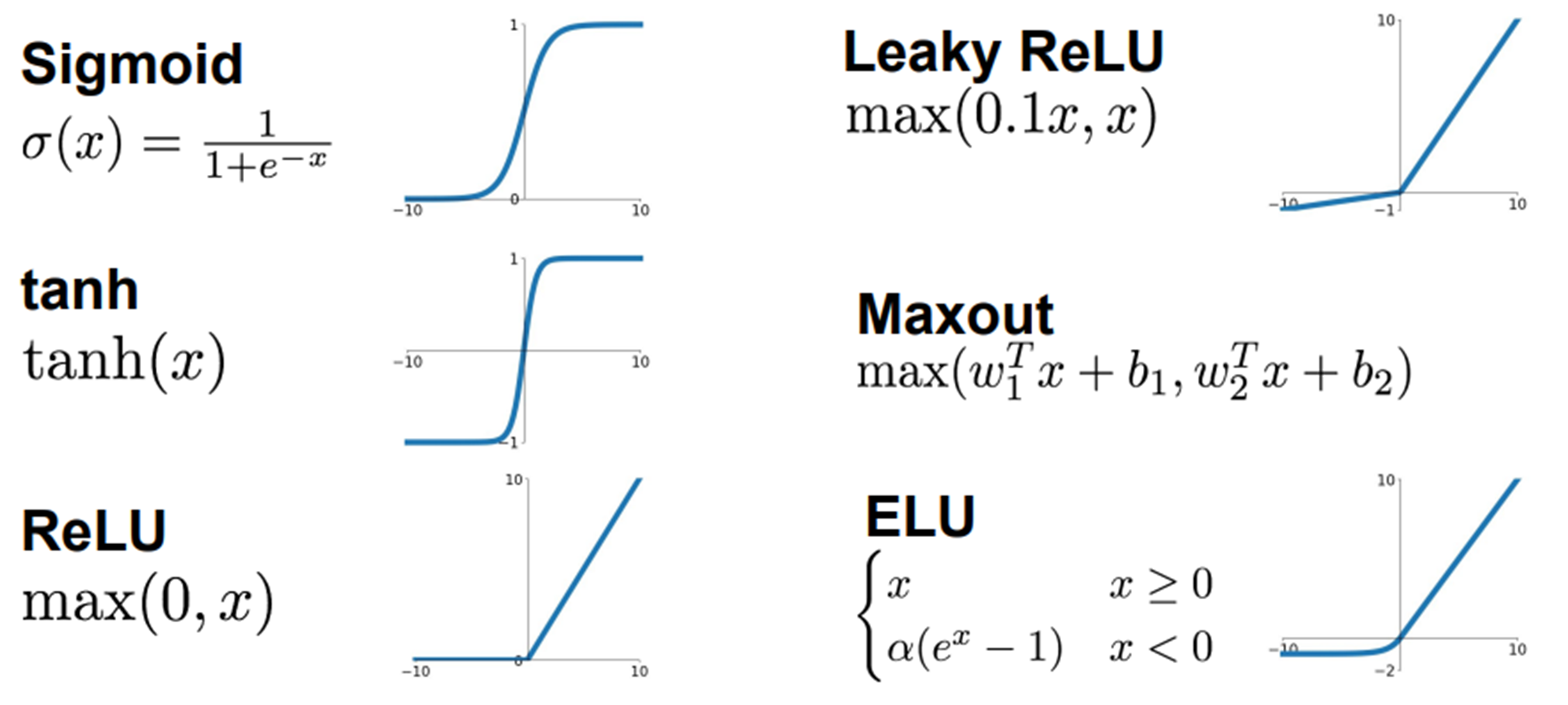
우리는 지난시간에 6개의 activation function을 배웠다.
이중에서 Sigmoid와 ReLU만 다시 봐보자!
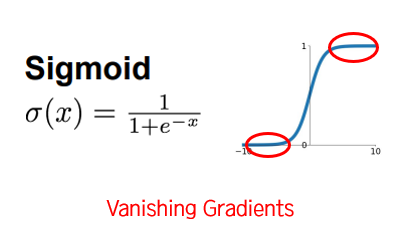
Sigmoid는 과거에 유명했지만 Vanishing Gradients의 문제점 때문에 이제는 잘 쓰지 않는다.

이제는 ReLU를 쓰는 것이 가장 좋은 보편적인 선택이다.
1-2) Weight Initialization

가중치를 지나치게 작게 초기화하면?
➡️ 작은 값이 계속해서 곱해지므로 gradient가 0이 된다.
➡️ 모든 activation이 0이 되고 학습은 이루어지지 않는다.
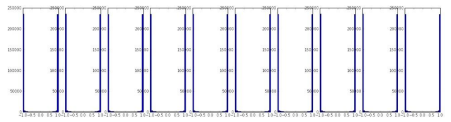
가중치를 지나치게 크게 초기화하면?
➡️ 큰 값이 계속해서 곱해지므로 activation이 saturate
➡️ gradient는 0이 되고 학습은 이루어지지 않는다.
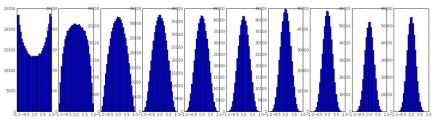
Xavier/MSRA Initialization을 사용해 가중치 초기화를 잘해주면?
➡️ activation 분포를 좋게 유지할 수 있다.
➡️ 학습이 잘 이루어진다.
Network가 깊어질수록 가중치를 더 많이 곱하게 된다.
➡️ 가중치 초기화는 Network가 깊어질수록 더 중요!!
1-3) Data Preprocessing
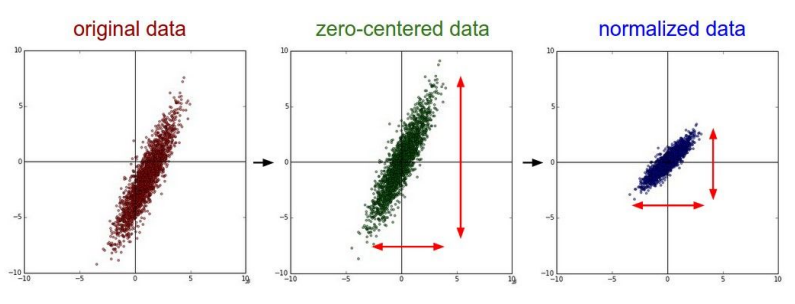
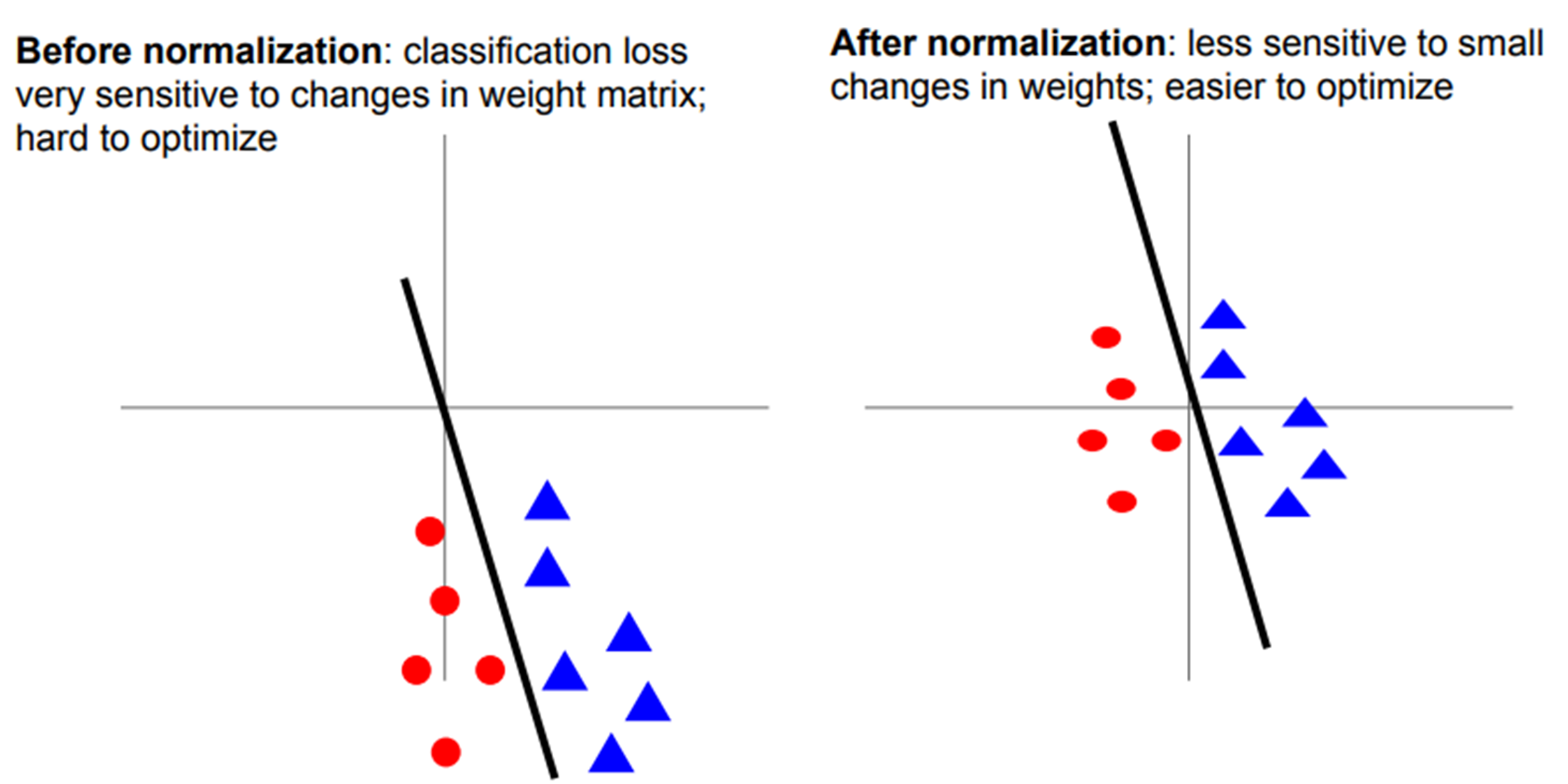
데이터 전처리를 통해 zero-mean, unit variance
➡️ 손실 함수가 가중치의 변동에 덜 민감하다.
➡️ 최적화, 학습이 더 쉽다.
1-4) Batch Normalization
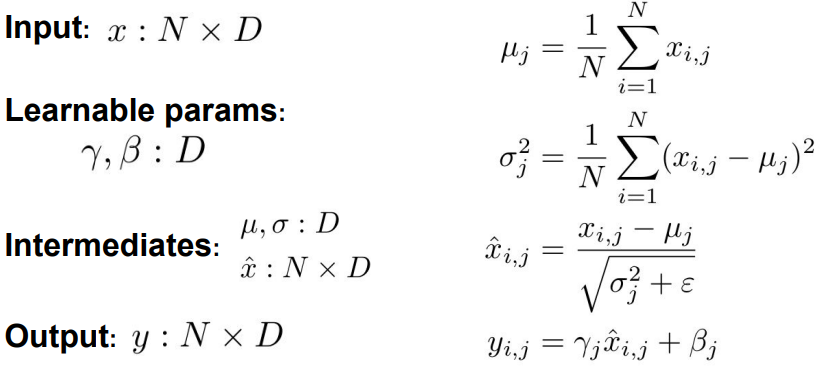
- Gradient vanishing이 발생하지 않도록 하기 위해 나온 아이디어
- activation이 unit gaussian(0과 1사이)이 될 수 있도록 레이어를 하나 추가하는 방법
- mini-batch마다 mean, variance를 계산하고, 이 값을 이용해 normalize
- scale, shift 파라미터
1-5) Babysitting Learning
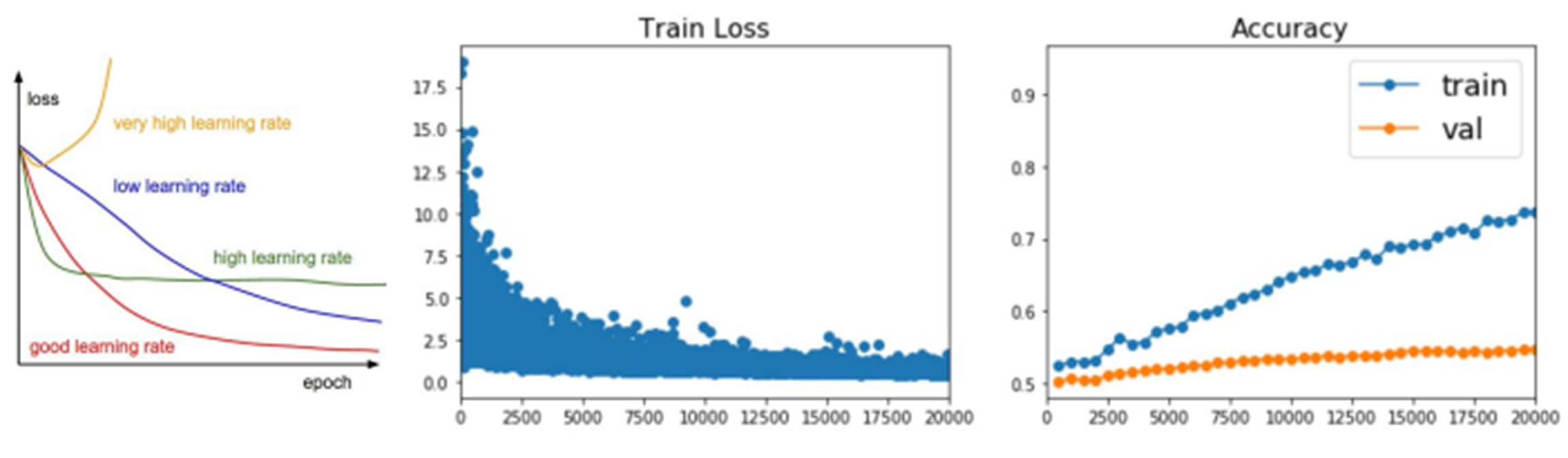
train set 성능 계속 올라감 & loss 줄고 있음
but, val 침체중!
➡️ 학습이 overfitting된 것. Regularization 필요!!
1-6) Hyperparameter Search
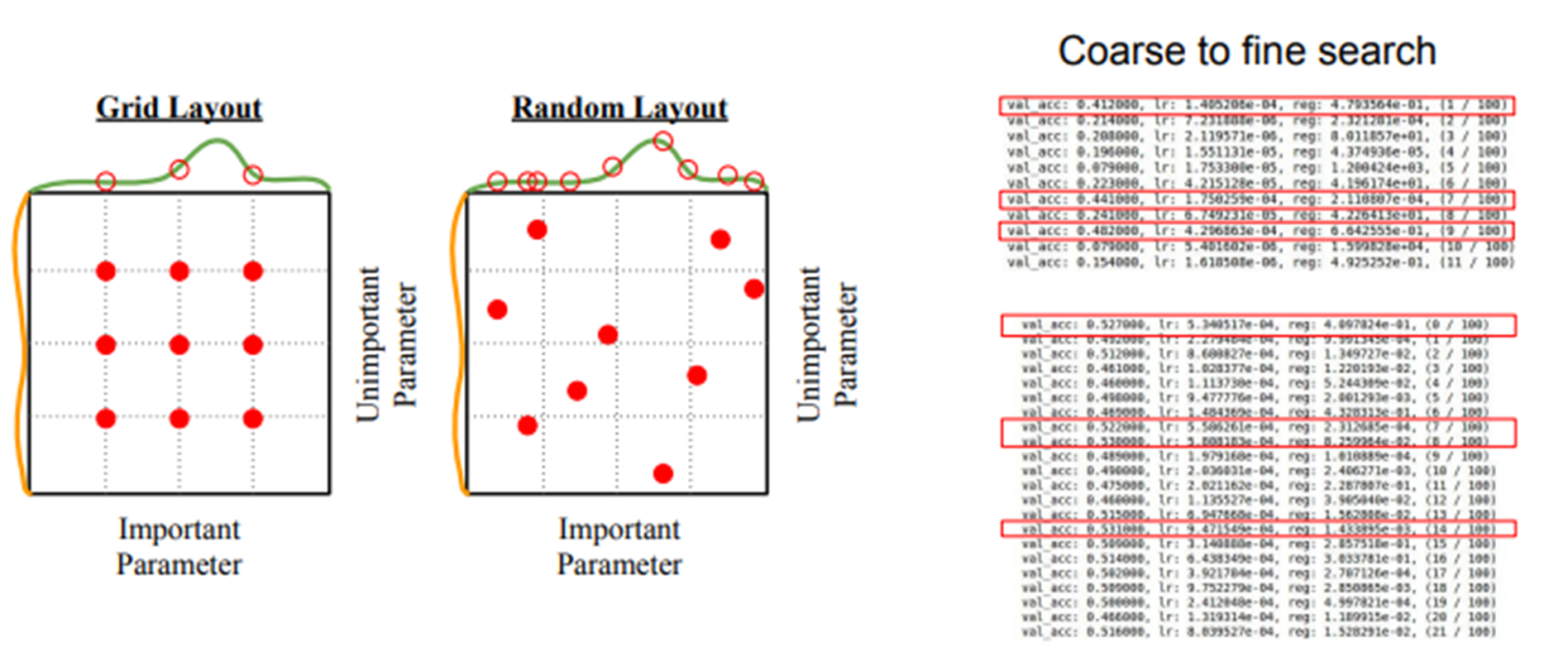
- Grid search 보다 Random search를 더 많이 사용한다.
- 적절한 하이퍼파라미터를 찾아야 train이 잘 이루어진다.
2. Optimization
2-1) SGD(Stochastic Gradient Descent)
가장 간단한 최적화 알고리즘
- mini batch 안에 있는 data의 loss를 계산한다.
- gradient의 반대 방향을 이용하여 update한다.
1,2의 과정을 반복한다.
SGD 문제점
1. jittering
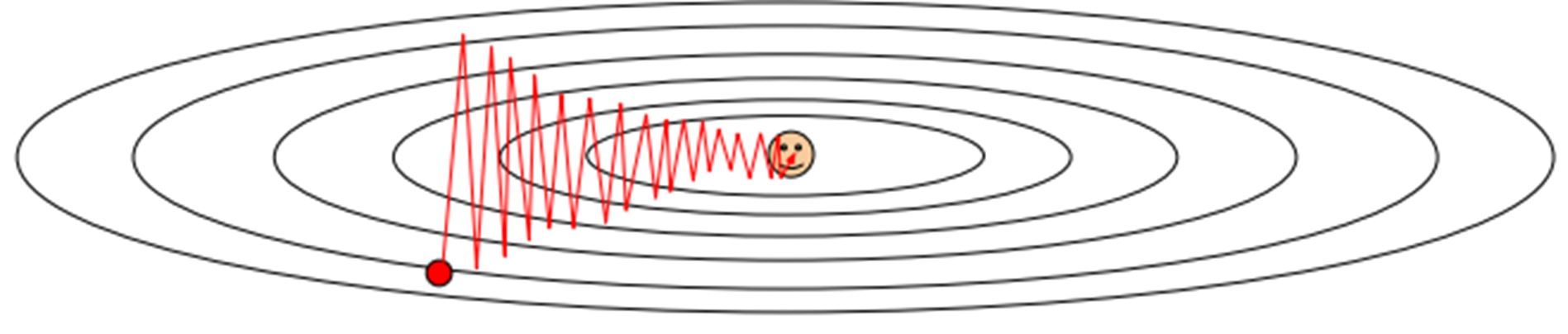
loss 방향이 한 방향으로만 빠르게 바뀌고 반대 방향으로는 느리게 바뀌면?
➡️ 불균형한 방향이 존재해 SGD는 잘 작동하지 않는다.
2. Local Minima & Saddle Point
x축은 하나의 가중치, y축은 loss
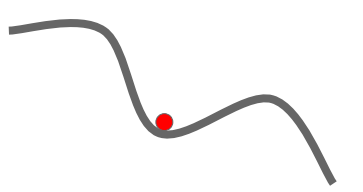
휘어진 손실함수의 중간에 local minima가 있다.
➡️ 순간적으로 기울기가 0이 되어 SGD는 멈춘다.
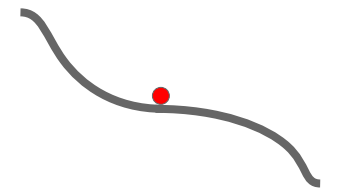
한쪽 방향으로는 증가하고 다른 방향으로는 감소하는 saddle point가 이싿.
➡️ 마찬가지로 순간적으로 기울기가 0이 되어 SGD는 멈춘다.
3. Noise
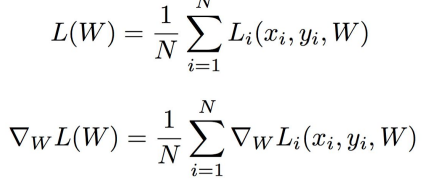
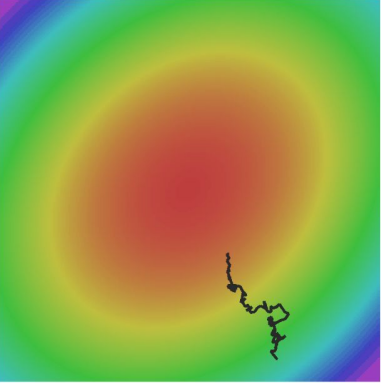
minibatches에서 gradient 값이 노이즈에 의해 많이 변할 수 있다.
아래의 그림처럼 gradient가 꼬불꼬불하게 update될 수 있다.
2-2) SGD + Momentum
앞서 본 SGD의 문제점들을 해결하기 위해 Momentum이라는 개념이 도입되었다.

Momentum은 기울기가 0인 지점에 빠지더라도 가속도로 탐색을 진행하도록 SGD에서 gradient를 계산할 때 velocity를 추가하는 방법이다.
기존 SGD에서 momentum의 비율인 하이퍼파라미터 rho가 추가되었다.
2-3) Nesterov Momentum

