최소 신장 트리의 이해
1. 프림 알고리즘 (Prim's algorithm)
- 대표적인 최소 신장 트리 알고리즘
- Kruskal’s algorithm (크루스칼 알고리즘), Prim's algorithm (프림 알고리즘)
- 프림 알고리즘
- 시작 정점을 선택한 후, 정점에 인접한 간선중 최소 간선으로 연결된 정점을 선택하고, 해당 정점에서 다시 최소 간선으로 연결된 정점을 선택하는 방식으로 최소 신장 트리를 확장해가는 방식
- Kruskal's algorithm 과 Prim's algorithm 비교
- 둘다, 탐욕 알고리즘을 기초로 하고 있음 (당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)
- Kruskal's algorithm은 가장 가중치가 작은 간선부터 선택하면서 MST를 구함
- Prim's algorithm은 특정 정점에서 시작, 해당 정점에 연결된 가장 가중치가 작은 간선을 선택, 간선으로 연결된 정점들에 연결된 간선 중에서 가장 가중치가 작은 간선을 택하는 방식으로 MST를 구함
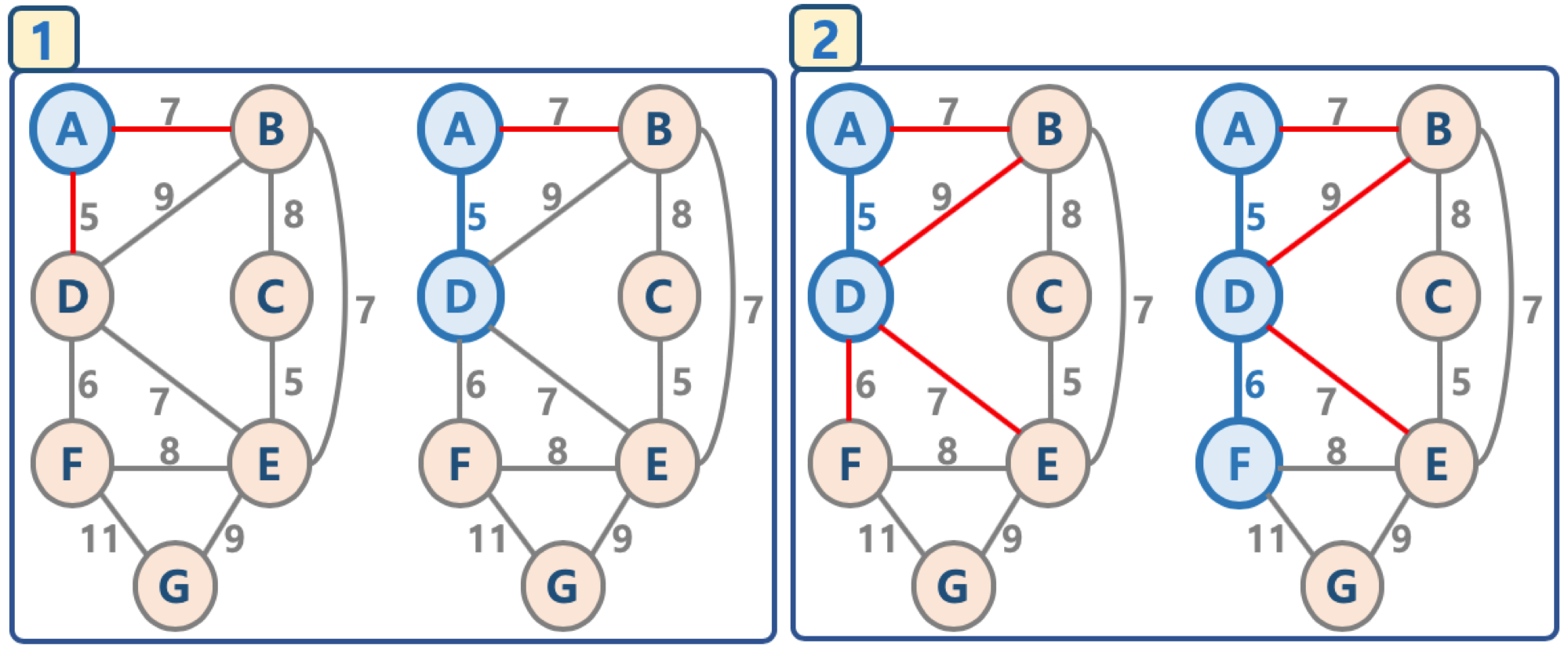
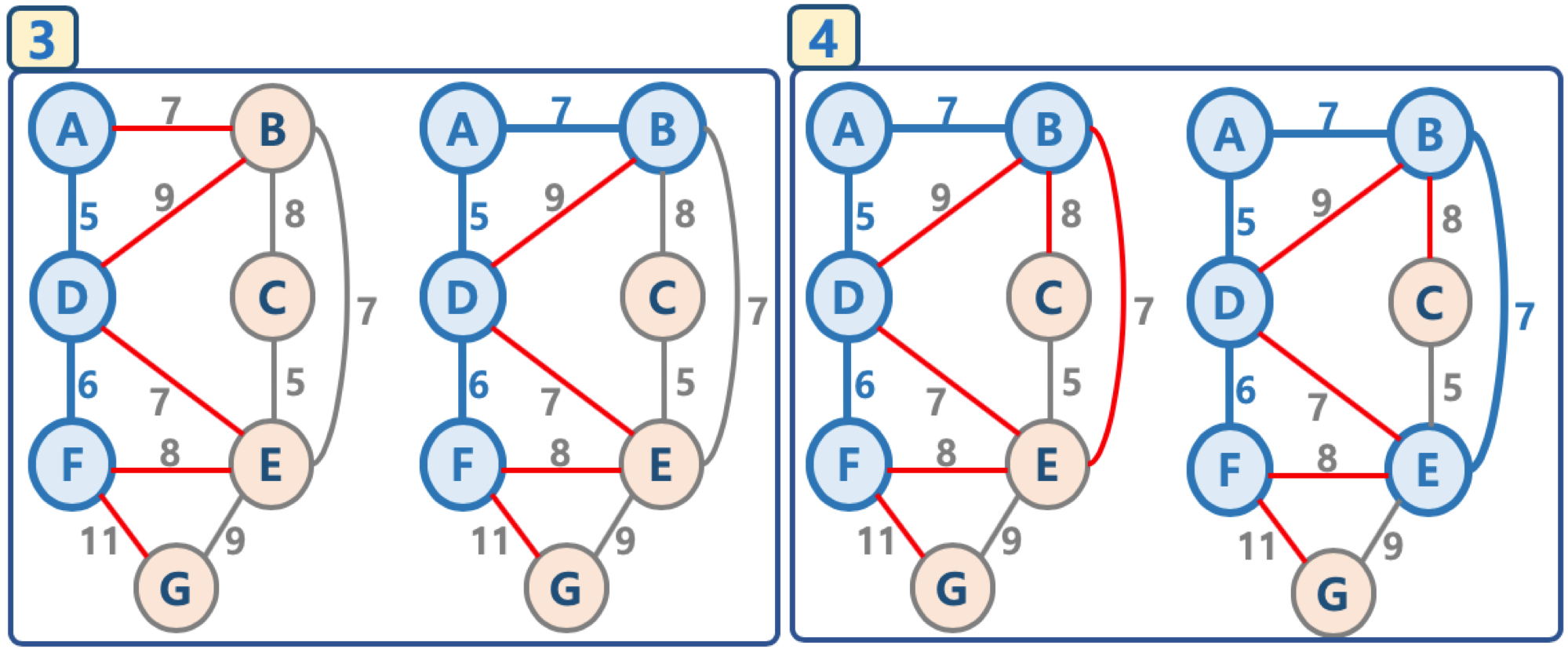
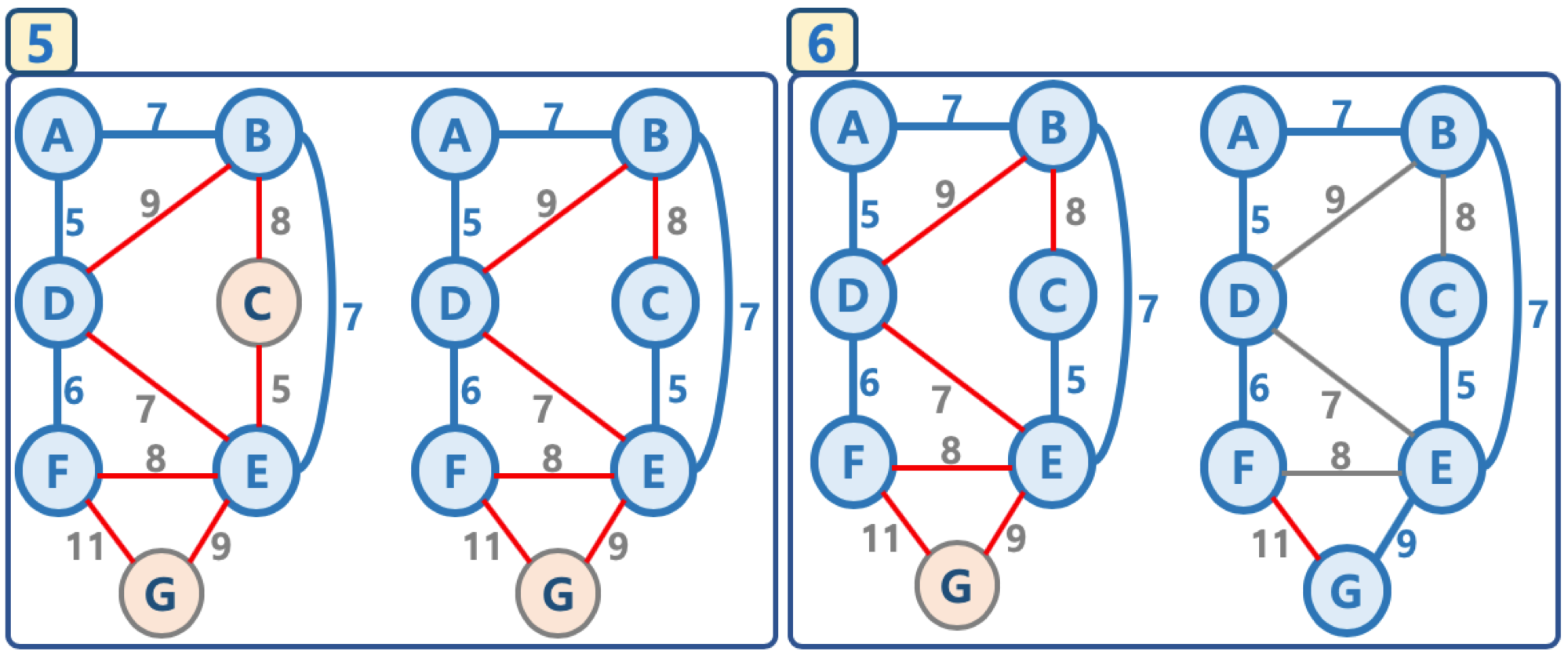
2. 그림으로 이해하는 프림 알고리즘
- 임의의 정점을 선택, '연결된 노드 집합'에 삽입
- 선택된 정점에 연결된 간선들을 간선 리스트에 삽입
- 간선 리스트에서 최소 가중치를 가지는 간선부터 추출해서,
- 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 이미 들어 있다면, 스킵함(cycle 발생을 막기 위함)
- 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 들어 있지 않으면, 해당 간선을 선택하고, 해당 간선 정보를 '최소 신장 트리'에 삽입
- 추출한 간선은 간선 리스트에서 제거
- 간선 리스트에 더 이상의 간선이 없을 때까지 3-4번을 반복
3. 프림 알고리즘 (Prim's algorithm) 코드 작성
참고: heapq 라이브러리 활용을 통해 우선순위 큐 사용하기
- heapq.heappush를 통해 데이터를 heap 형태로 넣을 수 있음 (0번 인덱스를 우선순위로 인지함)
import heapq
queue = []
graph_data = [[2, 'A'], [5, 'B'], [3, 'C']]
for edge in graph_data:
heapq.heappush(queue, edge)
for index in range(len(queue)):
print (heapq.heappop(queue))
print (queue)[2, 'A']
[3, 'C']
[5, 'B']
[]- heapq.heapify() 함수를 통해 리스트 데이터를 heap 형태로 한 번에 변환할 수 있음 (0번 인덱스를 우선순위로 인지함)
import heapq
graph_data = [[2, 'A'], [5, 'B'], [3, 'C']]
heapq.heapify(graph_data)
for index in range(len(graph_data)):
print (heapq.heappop(graph_data))
print (graph_data)[2, 'A']
[3, 'C']
[5, 'B']
[]참고: collections 라이브러리의 defaultdict 함수 활용하기
- defaultdict 함수를 사용해서, key에 대한 value를 지정하지 않았을 시, 빈 리스트로 초기화하기
from collections import defaultdict
list_dict = defaultdict(list)
print (list_dict['key1'])[]프림 알고리즘 파이썬 코드
- 모든 간선 정보를 저장 (adjacent_edges)
- 임의의 정점을 선택, '연결된 노드 집합(connected_nodes)'에 삽입
- 선택된 정점에 연결된 간선들을 간선 리스트(candidate_edge_list)에 삽입
- 간선 리스트(candidate_edge_list)에서 최소 가중치를 가지는 간선부터 추출해서,
- 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 이미 들어 있다면, 스킵함(cycle 발생을 막기 위함)
- 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 들어 있지 않으면, 해당 간선을 선택하고, 해당 간선 정보를 '최소 신장 트리(mst)'에 삽입
- 해당 간선에 연결된 인접 정점의 간선들 중, '연결된 노드 집합(connected_nodes)' 에 없는 노드와 연결된 간선들만 간선 리스트(candidate_edge_list) 에 삽입
- '연결된 노드 집합(connected_nodes)' 에 있는 노드와 연결된 간선들을 간선 리스트에 삽입해도, 해당 간선은 스킵될 것이기 때문임
- 어차피 스킵될 간선을 간선 리스트(candidate_edge_list)에 넣지 않으므로 해서, 간선 리스트(candidate_edge_list)에서 최소 가중치를 가지는 간선부터 추출하기 위한 자료구조 유지를 위한 effort를 줄일 수 있음 (예, 최소힙 구조 사용)
- 해당 간선에 연결된 인접 정점의 간선들 중, '연결된 노드 집합(connected_nodes)' 에 없는 노드와 연결된 간선들만 간선 리스트(candidate_edge_list) 에 삽입
- 선택된 간선은 간선 리스트에서 제거
- 간선 리스트에 더 이상의 간선이 없을 때까지 3-4번을 반복
myedges = [
(7, 'A', 'B'), (5, 'A', 'D'),
(8, 'B', 'C'), (9, 'B', 'D'), (7, 'B', 'E'),
(5, 'C', 'E'),
(7, 'D', 'E'), (6, 'D', 'F'),
(8, 'E', 'F'), (9, 'E', 'G'),
(11, 'F', 'G')
]from collections import defaultdict
from heapq import *
def prim(start_node, edges):
mst = list()
adjacent_edges = defaultdict(list)
for weight, n1, n2 in edges:
adjacent_edges[n1].append((weight, n1, n2))
adjacent_edges[n2].append((weight, n2, n1))
connected_nodes = set(start_node)
candidate_edge_list = adjacent_edges[start_node]
heapify(candidate_edge_list)
while candidate_edge_list:
weight, n1, n2 = heappop(candidate_edge_list)
if n2 not in connected_nodes:
connected_nodes.add(n2)
mst.append((weight, n1, n2))
for edge in adjacent_edges[n2]:
if edge[2] not in connected_nodes:
heappush(candidate_edge_list, edge)
return mstprim ('A', myedges)[(5, 'A', 'D'),
(6, 'D', 'F'),
(7, 'A', 'B'),
(7, 'B', 'E'),
(5, 'E', 'C'),
(9, 'E', 'G')]4. 시간 복잡도
- 최악의 경우, while 구문에서 모든 간선에 대해 반복하고, 최소 힙 구조를 사용하므로 O() 시간 복잡도를 가짐
참고: 개선된 프림 알고리즘
-
간선이 아닌 노드를 중심으로 우선순위 큐를 적용하는 방식
- 초기화 - 정점:key 구조를 만들어놓고, 특정 정점의 key값은 0, 이외의 정점들의 key값은 무한대로 놓음. 모든 정점:key 값은 우선순위 큐에 넣음
- 가장 key값이 적은 정점:key를 추출한 후(pop 하므로 해당 정점:key 정보는 우선순위 큐에서 삭제됨), (extract min 로직이라고 부름)
- 해당 정점의 인접한 정점들에 대해 key 값과 연결된 가중치 값을 비교하여 key값이 작으면 해당 정점:key 값을 갱신
- 정점:key 값 갱신시, 우선순위 큐는 최소 key값을 가지는 정점:key 를 루트노드로 올려놓도록 재구성함 (decrease key 로직이라고 부름)
-
개선된 프림 알고리즘 구현시 고려 사항
- 우선순위 큐(최소힙) 구조에서, 이미 들어가 있는 데이터의 값 변경시, 최소값을 가지는 데이터를 루트노드로 올려놓도록 재구성하는 기능이 필요함
- 구현 복잡도를 줄이기 위해, heapdict 라이브러리를 통해, 해당 기능을 간단히 구현
from heapdict import heapdict
def prim(graph, start):
mst, keys, pi, total_weight = list(), heapdict(), dict(), 0
for node in graph.keys():
keys[node] = float('inf')
pi[node] = None
keys[start], pi[start] = 0, start
while keys:
current_node, current_key = keys.popitem()
mst.append([pi[current_node], current_node, current_key])
total_weight += current_key
for adjacent, weight in mygraph[current_node].items():
if adjacent in keys and weight < keys[adjacent]:
keys[adjacent] = weight
pi[adjacent] = current_node
return mst, total_weightmygraph = {
'A': {'B': 7, 'D': 5},
'B': {'A': 7, 'D': 9, 'C': 8, 'E': 7},
'C': {'B': 8, 'E': 5},
'D': {'A': 5, 'B': 9, 'E': 7, 'F': 6},
'E': {'B': 7, 'C': 5, 'D': 7, 'F': 8, 'G': 9},
'F': {'D': 6, 'E': 8, 'G': 11},
'G': {'E': 9, 'F': 11}
}
mst, total_weight = prim(mygraph, 'A')
print ('MST:', mst)
print ('Total Weight:', total_weight)MST: [['A', 'A', 0], ['A', 'D', 5], ['D', 'F', 6], ['A', 'B', 7], ['D', 'E', 7], ['E', 'C', 5], ['E', 'G', 9]]
Total Weight: 39개선된 프림 알고리즘의 시간 복잡도: $ O(ElogV) $
-
최초 key 생성 시간 복잡도: $ O(V) $
-
while 구문과 keys.popitem() 의 시간 복잡도는 $ O(VlogV) $
- while 구문은 V(노드 갯수) 번 실행됨
- heap 에서 최소 key 값을 가지는 노드 정보 추출 시(pop)의 시간 복잡도: $ O(logV) $
-
for 구문의 총 시간 복잡도는 $ O(ElogV) $
- for 구문은 while 구문 반복시에 결과적으로 총 최대 간선의 수 E만큼 실행 가능 $ O(E) $
- for 구문 안에서 key값 변경시마다 heap 구조를 변경해야 하며, heap 에는 최대 V 개의 정보가 있으므로 $ O(logV) $
일반적인 heap 자료 구조 자체에는 본래 heap 내부의 데이터 우선순위 변경시, 최소 우선순위 데이터를 루트노드로 만들어주는 로직은 없음. 이를 decrease key 로직이라고 부름, 해당 로직은 heapdict 라이브러리를 활용해서 간단히 적용가능
-
따라서 총 시간 복잡도는 $ O(V + VlogV + ElogV) $ 이며,
- O(V)는 전체 시간 복잡도에 큰 영향을 미치지 않으므로 삭제,
- E > V 이므로 (최대 $ V^2 = E $ 가 될 수 있음), $ O((V + E)logV) $ 는 간단하게 $ O(ElogV) $ 로 나타낼 수 있음