1. 코사인 유사도 개념
코사인 유사도(Cosine Similarity)란 두 벡터 사이의 각도를 계산하여 두 벡터가 얼마나 유사한지 측정하는 척도입니다. 즉, DTM, TF-IDF, Word2Vec 등과 같이 단어를 수치화하여 표현할 수 있다면 코사인 유사도를 활용하여 문서 간 유사도를 비교하는 게 가능합니다. 코사인 유사도는 1에 가까울수록 두 벡터가 유사하다고 해석하며, 문서의 길이가 다른 경우에도 비교적 공정하게 비교할 수 있다는 장점이 있습니다. 아래 그림 1과 같이 두 벡터가 같은 방향을 가리키는, 즉 두 벡터 사이의 각도가 0일 때 코사인 유사도가 최댓값인 1을 갖습니다.
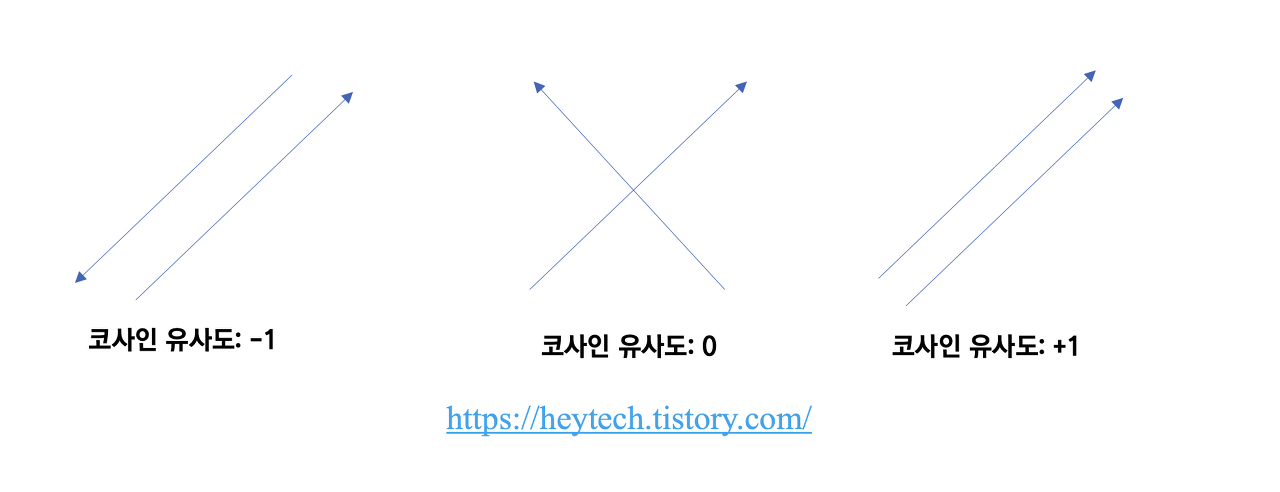
그림 1. 코사인 유사도
A, B라는 두 벡터가 있을 때 코사인 유사도 수식은 아래와 같습니다.
2. 코사인 유사도 실습
문서 예시
아래와 같은 3가지 문서가 있다고 해보겠습니다. 파이썬을 활용하여 코사인 유사도를 계산하고 문서 간 유사도를 비교해 보겠습니다.
| 구분 | 문장 |
|---|---|
| 문서1 | 나는 아침보다 저녁이 좋다 |
| 문서2 | 사과는 아침보다 저녁이 좋다 |
| 문서3 | 사과는 점심 간식으로 좋다 |
띄어쓰기를 기준으로 토큰화를 진행한다고 가정해 보겠습니다. 문서-단어 행렬(Document Term Matirx, DTM)을 표현하면 아래 표와 같습니다.
| 나는 | 아침보다 | 저녁이 | 좋다 | 사과는 | 점심 | 간식으로 | |
|---|---|---|---|---|---|---|---|
| 문서1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 문서2 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 문서3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
파이썬 코드
Step 1. 패키지 불러오기
import numpy as np
from numpy import dot
from numpy.linalg import norm필요한 패키지를 import합니다. numpy 패키지를 활용하면 벡터 표현, 연산을 쉽게 할 수 있습니다.
Step 2. 코사인 유사도 계산 함수
def cosine_similarity(A, B):
return dot(A, B)/(norm(A)*norm(B))수식을 고려하여 코사인 유사도를 계산하는 함수를 작성합니다.
Step 3. 문서-단어 행렬(DTM) 세팅
doc1 = np.array([1,1,1,1,0,0,0])
doc2 = np.array([0,1,1,1,1,0,0])
doc3 = np.array([0,0,0,1,1,1,1])문서 예시를 DTM으로 표현한 대로 준비합니다. 물론, 워드임베딩 기법을 사용하실 수 있다면 위와 같이 수기로 작성하실 필요는 없습니다. 간단한 예제이므로 수기로 작성해 봤습니다.
Step 4. 문서 간 유사도 확인
print(f"1. 문서1-문서2 간 유사도: {cosine_similarity(doc1, doc2)}")
print(f"2. 문서1-문서3 간 유사도: {cosine_similarity(doc1, doc3)}")
print(f"3. 문서2-문서3 간 유사도: {cosine_similarity(doc2, doc3)}")문서 간 유사도를 비교해 보면 아래와 같은 결과를 얻을 수 있습니다.
1. 문서1-문서2 간 유사도: 0.75
2. 문서1-문서3 간 유사도: 0.25
3. 문서2-문서3 간 유사도: 0.5실제 텍스트를 통해 문서를 비교해봐도 이렇게 계산한 유사도 값이 어느 정도 타당하다는 것을 아실 수 있습니다.