TIL 2024/7/15

Sung Joo Lee·2024년 1월 23일

재시작

정글이 끝나고 난 뒤 노션에다 정리한 내용을 복습하며 벨로그에 옮겨 쓰기로 했다. 앞으로 오래 걸리겠지만 꾸준히 옮기며 정리해 보도록 하겠다.

~~(새로운 내용의 공부는 노션에 먼저 정리하고 벨로그에 복습하는 방식으로 사용 할 것 같다..)~~

조합

파이썬에서 '조합'을 사용하여 문제를 해결 할 때 사용한다.

from itertools import combinations

Graph

그래프(graph)는 vertex와 edge로 구성된 한정된 자료구조를 의미한다. vertex는 정점, edge는 정점과 정점을 연결하는 간선이다.

일단 그래프를 표현하기 이전에 간단한 용어를 알아보자

Node(Vertex): 그래프에서 '점'을 나타낸다.
edge : Node와 Node를 연결 해 주는 '간선'으로 각 Node 간의 관계를 나타낸다.
인접 노드 : 특정 Node를 기준으로 Edge로 연결 되어있는 Node를 의미한다.
차수 (Degree) : 특정 Node에 연결된 Edge의 갯수를 말한다. '방향 그래프'와 '무방향 그래프'의 따라서 달라진다.
- 방향 그래프 : 말 그대로 Node 와 Node 사이에 방향이 존재 한다.
  - 이 때 '간선'의 수는 총 간선의 갯수와 동일하다.
- 무 방향 그래프 : Node와 Node 사이에 방향이 존재하지 않음.
  - 이 때 '간선'의 수는 총 간선의 '갯수 X 2'를 해준다.

그래프 G =(V,E) 표현하기 위한 두 가지 방법

인접 리스트의 집합

인접 행렬

두 방법 모두 방향,무방향 그래프에 적용할 수 있다.

인접 리스트

연결 관계를 1차원 배열 리스트을 사용하여 나타낸다.

adj[i] : i번째 노드에 연결된 노드들을 원소로 갖는 리스트

최대 가능한 edge의 수에 비해 edge의 수가 적은 그래프에 유용

인접 리스트 또한 무방향 그래프의 경우에는 본인 노드 인덱스의 리스트 내에 서로를 원소로 가지게 된다.
인접 리스트를 활용하여 표현하는 방식

인접 리스트는 그래프의 전체 노드 목록을 저장한다.
Python에서는 하나의 노드가 키(key)가 되고, 그 노드에 인접한 노드가 값(value)이 되는 딕셔너리로 구현할 수 있다.
인접 리스트는 인접 행렬이 갖는 단점을 극복할 수 있다.

# 유향 그래프
n = 4
e = 5
nodes = [[1, 2], [1, 3], [1, 4], [2, 3], [3, 4]]

# 인접 리스트 초기화
adj = [[] for _ in range(n)]

# 엣지 추가 (방향 그래프)
for src, dst in nodes:
    adj[src-1].append(dst-1)

# 무향 그래프
n = 4
e = 5
edges = [[1, 2], [1, 3], [1, 4], [2, 3], [3, 4]]

adj = [[] for _ in range(n)]

for src, dst in nodes:
    adj[src-1].append(dst-1)
    adj[dst-1].append(src-1)

인접 리스트의 장점

실제 연결된 노드에 대한 정보만 저장,저장된 리스트 원소 개수가 간선의 개수와 동일
간선의 개수에 비례하는 메모리 차지
각 노드에 연결된 모든 노드들을 방문해 보아야 할 경우 행렬에 비하여 큰 시간상의 이점

인점 리스트의 단점

특정 노드의 연결 여부를 알고 싶을때 adj[i]를 순회하며 해당 vertex와 연결 되어있는지 확인해야함 -> O(V)

인접 행렬

그래프의 연결 관계를 행렬로 표현하여 이차원 배열 리스트로 나타내는 방식

ad[i][j]: 노드 i에서 j로 가는 간선이 존재할경우 1, 아니면 0

무향 그래프의 경우 노드 i에서 j로가는 길이 존재하면 노드 j에서 i로 가는 길 또한 존재한다. -> 대각 기준으로 대칭인 성질을 가지게 된다

예시)

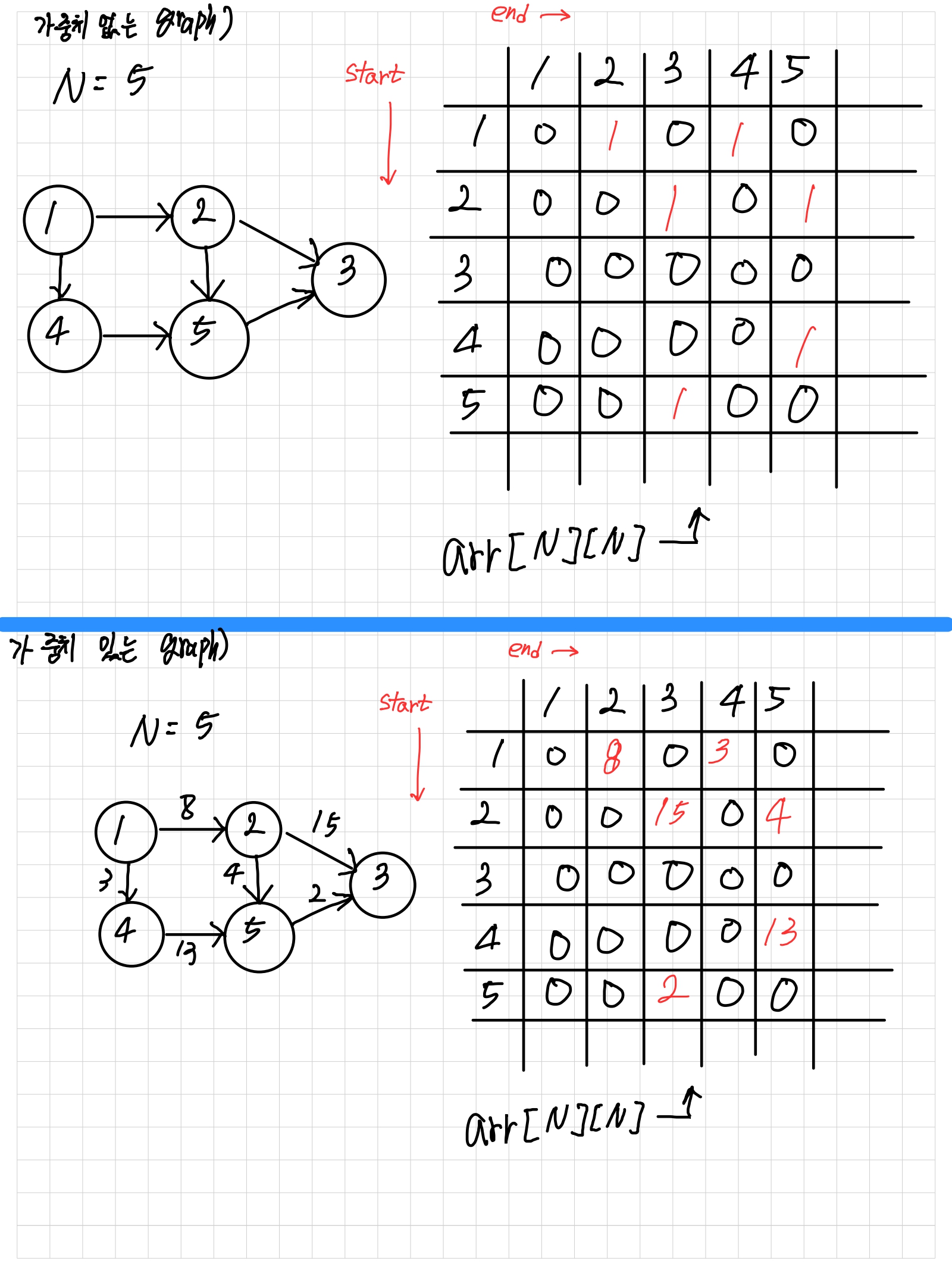
코드)

#방향 그래프

n = 4
e = 5
edge = [[1, 2], [1, 3], [1, 4], [2, 3], [3, 4]]

# 인접 행렬 초기화
adj = [[0 for _ in range(n)] for _ in range(n)]

# 엣지 추가 (방향 그래프)
for src, dst in edge:
    adj[src-1][dst-1] = 1

# 인접 행렬 출력
for row in adj:
    print(row)


# 무방향 그래프
n = 4
e = 5
edge = [[1, 2], [1, 3], [1, 4], [2, 3], [3, 4]]

adj = [[0 for _ in range(n)] for _ in range(n)]

for src, dst in edge:

    adj[src-1][dst-1] = 1

    adj[dst-1][src-1] = 1

인접 행렬 장점

구현이 비교적 쉬움, 특정 노드가 연결 되어있는지 확인할때 O(1)의 시간 복잡도 갖음
가중치 값을 바로 찾을 수 있음

인접 행렬 단점

전체 노드의 개수를 V개,간선의 개수를 E개 라고 할때 노드 i에 연결된 모든 노드들에 방문하고 싶으면 adj[i][1] ~ adj[i][V]까지 모두 확인해야해서 O(V)의 시간이 걸린다
- 즉, 노드에 비례해서 시간 복잡도,공간 복잡도가 높아진다
노드의 수에 비해 간선의 개수가 훨씬 적은 그래프면 적절하지 않다

~~인접 행렬로 풀 수 있는 문제는 인접 리스트로도 풀 수 있다~~

인접 행렬 vs 인접 리스트

인접 행렬
- 장점: 두 노드의 간선의 존재 여부를 바로 알 수 있음
- 단점: 모든 관계를 기록함으로 노드의 개수가 많을 수록 불필요한 메모리 낭비가 일어남
인접 리스트
- 장점: 연결된 것들만 기록함, 어떤 노드의 인접한 노드들을 바로 알 수 있음
- 단점: 두 노드가 연결되어 있는지 확인이 인접 행렬보다 느림