Data Structure(자료구조) 란?

자료구조란 데이터에 편리하게 접근하고, 변경하기 위해서 데이터를 저장하거나 조작하는 방법을 말한다.

만약에 사과를 담는 용기가 필요하다고 생각해보자. 사과를 멀리 가지고 가려는 목적이라면 바퀴가 달려있는 수레 같은게 필요할 수 있다. 자주자주 꺼내 먹기 위한 용기가 필요하다면 손을넣어 꺼낼수있는 백이나 바구니 같은 형태가 적합하다고 할수있겠다.
어떤 자료구조를 선택하느냐에 따라 퍼포먼스가 달라진다.

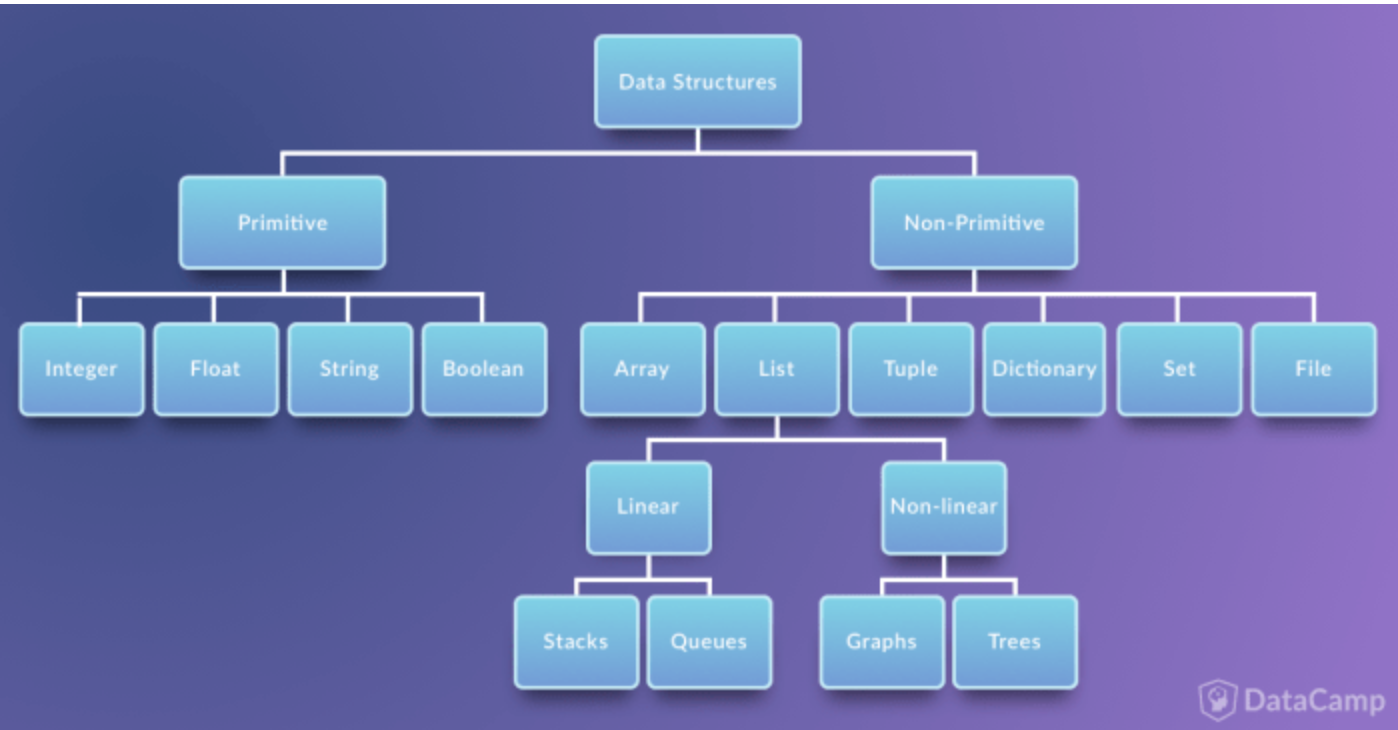
일반적으로 자주 사용되는 구조들

Array(List)

배열 데이터가 순차적으로 있는것
그 이유는 메모리상에 물리적으로 순차적으로 저장되기 때문이다.
인덱스가 있기 때문에 조회가 가능하다. (인덱스로 조회가 가능하다)
순차적인 데이터를 다루기 적절하다.
단점은 할당된 메모리가 다 사용되면 리사이징하기 때문에 그때 비용이 추가된다.
배열의 모든값을 순회하여 조회하기 때문에 서치가 느리다.
배열의 사이즈가 커질수록 더 느려진다 (0(N))
인덱스로 접근하는경우는 가장 빠르다(0(1))
*메모리 = 휘발성이다.프로그램을 실행할때 사용된다. 빠르다. 데이터의 영구저장은 하드디스크에 한다.

Tuple

List와 마찬가지로 데이터를 순차적으로 저장할 수 있는 순열 자료구조.
하지만 list와 틀리게 수정 할 수 없다 (immutable)
주로 2나 3개 정도의 소규모 데이터를 저정할 때 쓰입니다,
함수에서 리턴 값을 한개 이상 리턴 하고 싶을때 자주 쓰입니다.
Array나 list를 쓰기에 너무 간단한 데이터들을 표현할때.
Tuple이 list보다 더 가볍고 메모리더 적게 먹는다.
예를 들어, 좌표 데이터.

Set

Set는 array나 list 처럼 순열 자료구조 (collection) 입니다.
하지만 set는 순서라는 개념이 존재하지 않습니다. Set의 특징은 다음과 같습니다.
데이터를 비순차적(unordered)으로 저장할 수 있는 순열 자료구조 (collection).
삽입(insertion) 순서대로 저장되지 않는다. 즉 특정한 순서를 기대할 수 없는 자료구조.
수정 가능하다(mutable).
동일한 값을 여러번 삽입 불가능하다. 동일한 값이 여러번 삽입 되면 하나의 값만 저장된다.
Fast Lookup이 필요할때 주로 쓰인다.
중복된 값을 골라내야 할때
빠른 look up 을 해야 할때
그러면서 순서는 상관 없을때

Dictionary(object)

Dictionary (다른 언어에서는 hashmap 이나 hash table이라고 하기도 함)는 Key-value 형태의 값을 저장할 수 있는 자료구조 입니다. 이름은 "정우성" 등 실제 데이터 값과 데이터를 설명하는 key의 대응 관계를 표현할때 유용합니다.
Dictionary의 특성은 다음과 같습니다.

Set과 마찬가지로 특정 순서대로 데이터를 리턴하지 않는다.
Key의 값은 중복될 수 없다. 만일 중복된 key 가 있으면 먼저 있던 key와 value를 대체한다.
수정 가능하다(mutable).
마치 데이터베이스 처럼 키와 값을 묶어서 데이터를 표현해야 할때 유용하다. 실제로 데이터베이스 에서 읽어들인 값을 dictionary로 변환해서 사용 자주 함.

Stack & Queue

Stack은 LIFO(Last In First Out) 이라고 합니다. 마지막으로 저장한 데이터가 처음으로 읽힌다는 뜻입니다. 마치 설겆이 한 접시를 하나 하나 쌓아올리는걸 생각하시면 쉽습니다.

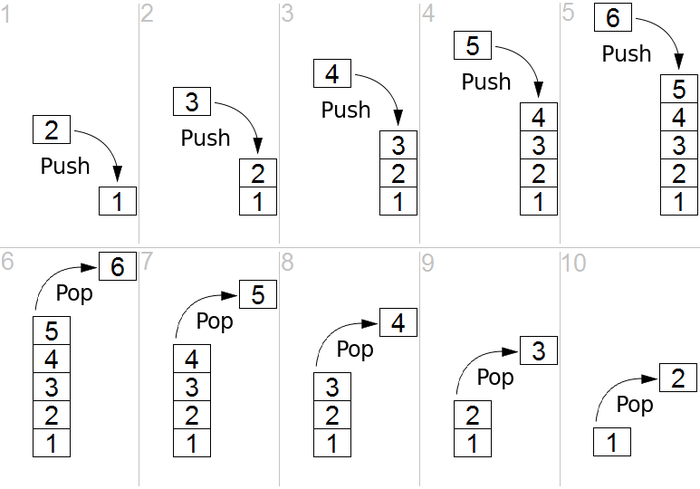
Stack에서 데이터 저장은 push 라고 합니다.
데이터를 읽어들이는 건 pop 이라고 합니다. 다만 pop은 읽어들임과 동시에 stack에서 삭제합니다.

Queue는 Stack과 반대로 FIFO(First In First Out) 입니다. 즉 먼저 push 된게 먼저 pop 된다는 말입니다.

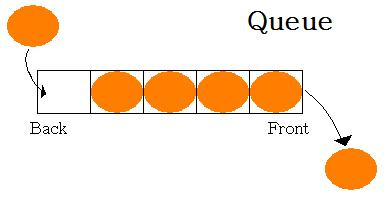
일반적인 queue 말고도 double ended queue, priority queue 등도 있습니다.
맛집 예약 시스템
OS 프로세스 스케쥴링 시스템 (priority queue 사용)

Tree

Tree 자료구조는 데이터를 마치 나무(거꾸로된) 형태로 저장하는 자료 구조 입니다. Tree 자료구조는 여러 유형이 있지만 그 중 가장 기본은 binary tree(이진 트리) 자료구조 입니다. 이진 트리는 두개의 자식 노드를 가진 트리 형태입니다.

이진 트리는 검색을 효율적으로 할 수 있습니다. 원하는 값을 찾을 때까지, 현재 node의 값이 원하는 값보다 크면 왼쪽으로, 작으면 오른쪽 으로 움직이면 됩니다.

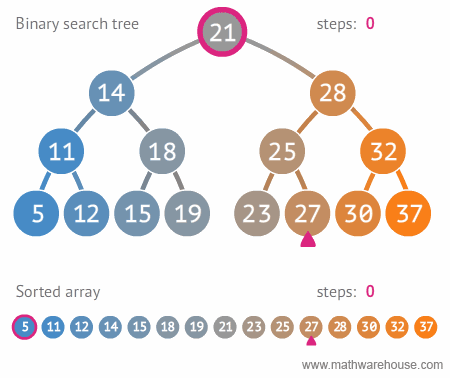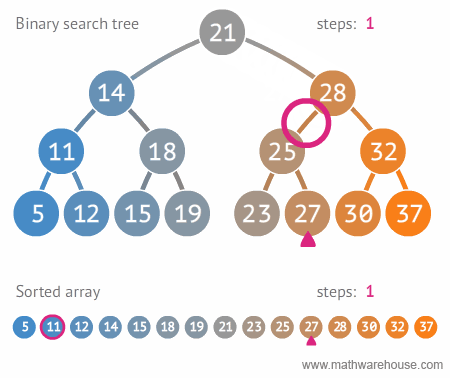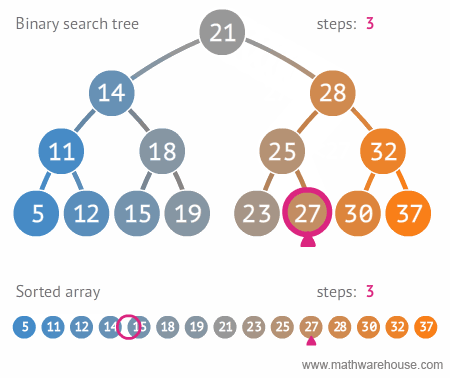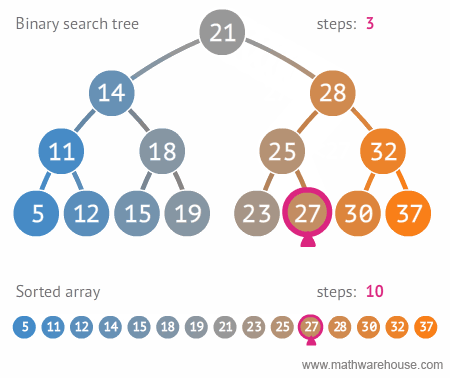
그럼으로 일반 list는 검색이 O(N)인데에 비해 이진 트리는 O(log N) 이므로 리스트 보다 검색이 훨씬 효율 적입니다.