Big O (2)

시간복잡도 / 공간복잡도 / 로그,세션 / 빅오 단순화

이제는 실제로 빅오에 대한 이해를 가지고 정의를 할 수 있어야한다.

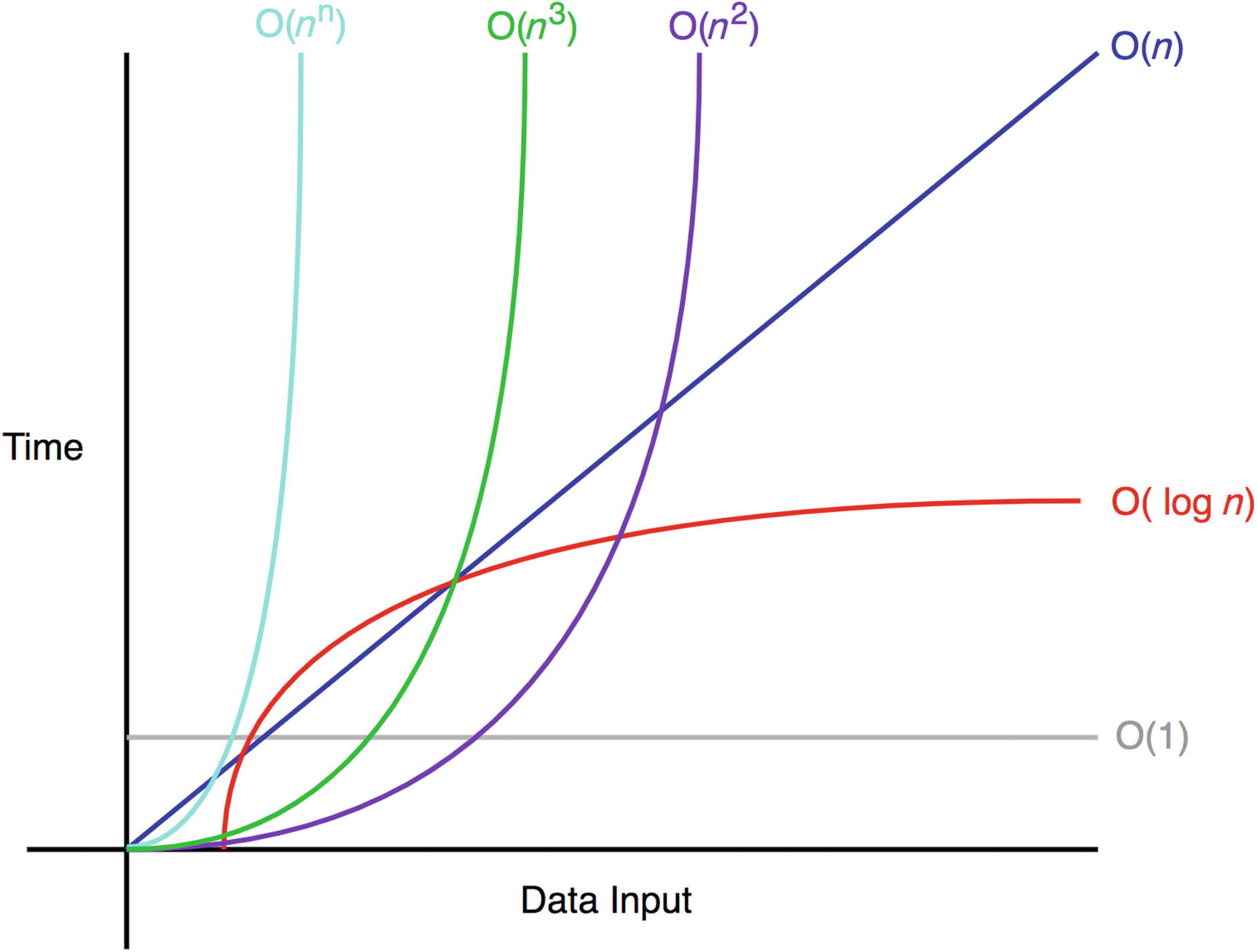
O(n)과 O(n^2)에 실행 속도를 생각해보자!

기본적으로 입력이 n이 커질수록 알고리즘이 얼마나 효율적인지 표현하는 방식이라는 것을 기억해둬야한다. 단순한 상수가 커지는 값이 아닌 n2그래프 처럼 수학적으로 접근할 수도 있다.

"입력인 n이 커질수록 알고리즘이 얼마나 효율적인지 표현하는 방식"

작은 연산이나 상수에 집중하는 것이 아닌 n,n^2, n^2 ... 크게 보고 효율을 찾아가려한다.(추세)

예시)

function check5(n) {
  for (var i = 1; i <= Math.max(5, n); i++) {
    console.log(i);
  }
}
check5(4);
console.log(check5(4));

O(n^2+5n+8) => O(n^2) 으로 볼 수 있다.

사실상 정확하지는 않지만 추세에서는 크게 벗어나지않는다는 것을 인지하자!

Big O shorthands

1. 상수, 연산은 상관없는 것(짧은 시간)으로 간주한다.
2. 객체를 다루고 배열, 데이터를 접근한기 위해서 키가 있다면 그것도 실행 시간이 상수일 것이다.
3. 데이터를 루프로 처리할때는 중첩루프가 있는지도

단순화하는 작업이라고 볼수있다.

I've been focusing on time complexity, run time.
How can i analyze the runtime of an algorithm as the size of the inputs increases?

입력이 커질수록 알고리즘이 얼마나 커질지 상상해보자.

공간과 사용되는 메모리에 집중하면서 문제들을 접근해야한다.
이것을 "공간복잡도"라고 말한다.

1. booleans, number, undefined, null 모두 불변 공간이라고 여긴다.(같은 공간차지)
2. 문자열은 O(n) 공간이 필요하다.
3. reference, 배열, 객체도 O(n)이라고 생각한다.

로그함수 / 지수함수