피보나치(Fibonacci) 수열을 구현하는 7가지 방법

피보나치 수열

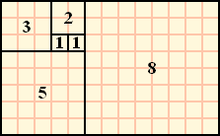
• 현재 값 f(t)를 구함에 있어서, 바로 이전의 값 f(t-1), 그 이전..이전..의 값 f(t-2)을 더하는 방법으로 수를 생성

  • 과거 2개의 값을 더해서, 현재 값을 만드는 방법
  • 이 계산을 계속 반복해 만드는 숫자들이 바로 '피보나치 수'

• 현재시간(t)의 함수를 f(t)로 표현

  $f(t) = f(t-1) + f(t-2)$

• 수열 예시

  • 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, .....

피보나치 수열을 구현하는 방법

1. 일반 함수 사용 방식(Function)

• 입력값 n을 넣어주면, loop문을 통하여 피보나치를 계산하고 결과값을 반환해 주는 방식

def fib(n):
    a,b = 1,1
    if n==1 or n==2:
        return 1
        
    for i in range(1,n):
        a,b = b, a+b

    return a

• '피보나치 수'가 아니라 '피보나치 수열'을 구하고 싶다면?
  • 파이썬(Python) 리스트 표현식 (List Comprehension)을 사용해서 출력
    [ fib(x) for x in range(1,10) ]

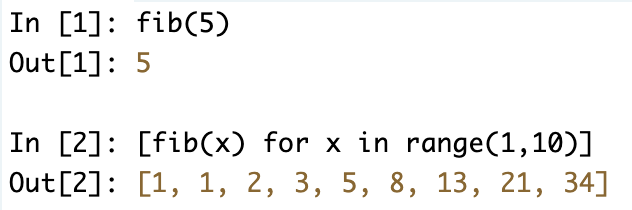
2. 재귀 함수 사용 방식(Recursive Function)

• 자기 자신을 다시 호출하는 자가증식(??) 방식의 코딩
  • 가장 중요한 점: 자가증식의 종료를 명시해야 함
  • 재귀함수의 종료 조건이 정확하지 않으면 무한 증식할 수 있음!
    (재귀함수의 가장 중요한 부분)

def fib(n):
    if n==1 or n==2:
        return 1
    else:
        return fib(n-1) + fib(n-2)


fib(5)

COMMENT
개인적으로 재귀함수 방식을 좋아하지는 않습니다. 과거에 메모리를 많이 아껴야 하는 시절에는 많이 사용되었습니다만, 메모리가 충분히 성장한 요즘 시대에는 학습차원에서 공부하는 것은 좋지만, 현장에서 사용은 꺼리고 있습니다. 이유는, 재귀함수를 사용하면 가독성이 떨어집니다. 또한, 만약 실수하면 무한루프에 빠지게 되죠. 나중에 디버깅도 쉽지 않습니다. (코딩 인계라도 하는 날이면,,,,, ㅜ_ㅜ)
그러나, 알고리즘 문제는 빠지지 않고 출제되니, 시험을 위해서라면 공부해 두세요~

3. 제네레이터 (Generator) 방식

• Generator는 단순 반복문(loop)이 아님!
  • yield를 사용하여, next가 호출 되었을 때만, 한 Step씩 진행하여 결과값을 반환해 주는 방식

def fibs():
    a,b = 0,1    // generator 출력할 때, next()로 다음것을 출력⇒ 한단계 늦춤
    while True:
        a,b = b, a+b
        yield a

f = fibs()
next(f)

Out[1]: 1

def fibs():
    a,b = 0,1
    while True:
        a,b = b, a+b
        yield a

f = fibs()
next(f)
next(f)
next(f)
next(f)
next(f)

Out[1]: 5

4. 메모이제이션 방식(Memoizatioin Method)

• 데이터의 중요성 때문에, 데이터를 Array에 넣어 놓고 계산하는 방식으로 바뀌고 있음

  • Bigdata를 처리하는 경우가 대부분 이런 경우에 해당
  • map / reduce 등의 방식이 대표적

• 피보나치 수열의 각 단계의 결과를 Array로 만들어 반환 하는 방식

  • 동적계획법 (Dynamic Programming) 접근 방법 중 하나
  • 동적계획법의 대표적인 예로 피보나치 수열이 자주 등장

• "반복되는 수는 메모리에 저장해 두고, 반복 계산 대신 저장해둔 값을 사용한다"

  • Fibonacci(5)를 계산하면, 하위의 fibonacci를 반복적으로 계산하는데, 여러 번 계산하지 말고 한번 계산하면 다음에는 그 결과를 재활용 하자는 컨셉

• 피보나치 수열의 반복 계산
  

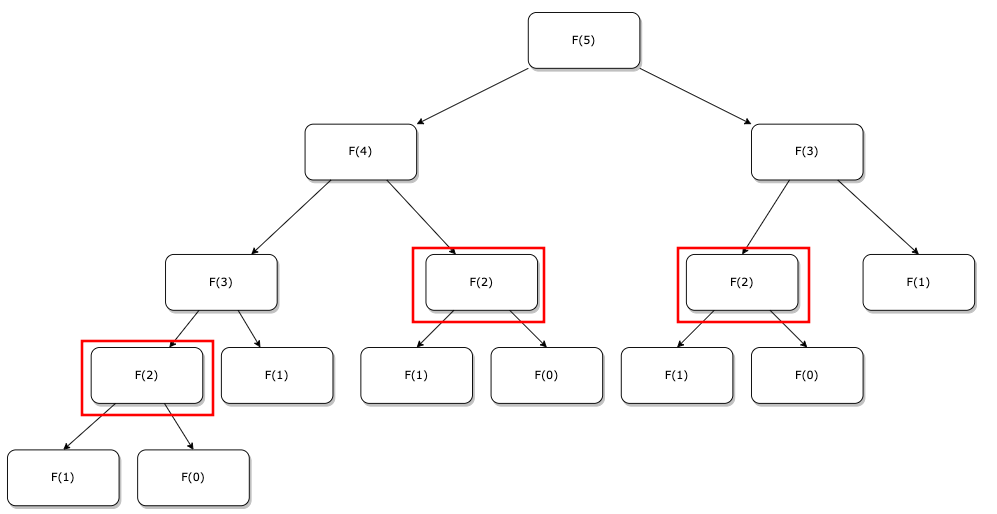
  • Fib(5)를 구할 때 반복적인 Fib(2)가 계산이 되고 있음
    • Fib(3), Fib(4) ... 계속 반복 계산하는 방식으로 이루어져 있음
  • 복잡도를 구하면 O($2^N$)에 해당
    • N이 늘어날 수록 Exponetial하게 연산량이 증가

• 동적계획법(Dynamic Programming)을 사용한 피보나치 수열 계산: BottomUp 방식
  

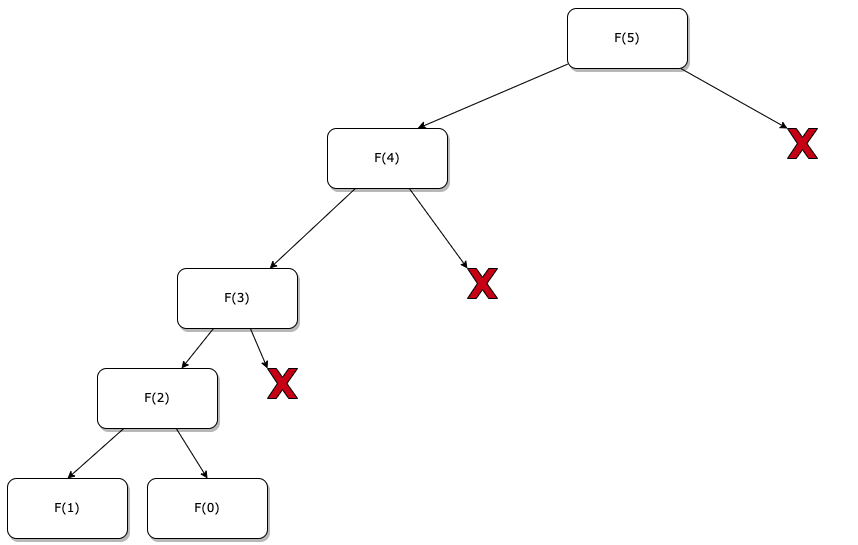
  • 효과적인 계산을 위해서, 이것을 한번 계산한 결과를 메모리에 저장해 두고 불러다 사용하는 방식을 취하면 연산량이 대폭 감소
  • 이러한 방식의 복잡도는 O(N)으로 효과적으로 연산량을 줄일 수 있음

• 동적계획법(Dynamic Programming: Bottom-Up 방식)으로 피보나치수열 구현

def fib(n):
    fibList=[1, 1]
    if n==1 or n==2:
        return 1
    for i in range(2,n):
        fibList.append( fibList[i-1] + fibList[i-2] )
    return fibList

fib(5)

Out[1]: [1, 1, 2, 3, 5]

5. 파이썬 한줄 코딩 (Single Line) 1

• Single Line Code with lambda
  • 파이썬의 lambda 함수를 이용하면, 다음과 같이 한 줄로 표현이 가능
  • 내부적으로는 재귀함수 호출을 람다 함수로 단순화 한것

fib = lambda n: 1 if n<=2 else fib(n-1) + fib(n-2)

fib(5)

6. 파이썬 한줄 코딩 (Single Line) 2

• 재귀호출되는 함수의 인자값에 넣어줄 때 원하는 계산을 수행 후 입력하는 방식

fib = lambda n, a=0, b=1 : a if n<=0 else fib(n-1,b, a+b)

fib(5)

7. 파이썬 행렬 연산 (Numpy)

• Matrix Operational method
  • 행렬 연산: 여러 개의 식을 하나의 묶음으로 계산하는 것
  • "계산들의 패키지"
• 피보나치를 위한 행렬 연산식
  
  • 어떤 행렬A에 행렬[ [1,1], [1,0] ] 을 곱하는 것은 각각을 더하거나, 원소를 그대로 가져오가나 등의 기능
  • 주의: Step이 하나 더 진행되었을 시점임을 고려해야 함
    • 곱하는 시점의 n은 다음 스텝의 n-1
    • 결과행에서 1행 2열의 값은, 1 F(n) + 1 F(n-1) → 결과행 시점에서, n-1번째 결과 + n-2번째 결과

A = np.matrix( [ [1,1], [1,0] ] )

(A**5)[0,1]