데이터 종류

1. 척도에 따른 데이터 종류

• 질적 데이터
  • 수치로 표현되지 않은 데이터(관측값)
    • 개체명, 개체가 속하는 범주명, 순서와 같이 관측 대상의 질적 정의를 의미
  • 명목척도와 순서척도를 사용하여 구한 데이터
    (명목척도와 순서척도로 관측한 관측값)
  • 수치가 아닌 기호로 표현
    • 숫자를 기호로 취급하여 개체의 이름(명목)을 정의하는 경우도 있음
• 양적 데이터

2. 속성에 따른 데이터 종류
3. 대상에 따른 데이터 종류
4. 가공에 따른 데이터 종류

모집단의 평균과 표준편차

• 평균

  • 데이터의 각 수치를 전부 더한 다음 개수로 나눔: 산술평균

• 모집단의 평균 = 모평균(μ, 뮤)

  • 모집단의 데이터에서 구해낸 평균
  • μ = (ΣX)/N
    • Σ(시그마): sum 연산 기호
    • X: 각 데이터 하나하나를 의미
    • N: 표집수, 데이터 개수
  • 모집단의 각 데이터를 다 더한 것을 데이터의 총 개수인 N으로 나눔

• 모집단의 표준편차(standard deviation)
  = 모표준편차(σ, 시그마)

• 모수치

  • 모집단의 데이터가 있을 때의 모평균과 모표준편차
  • 즉, μ와 σ
  • 현실에는 없다고 봐도 되는 데이터

표본의 평균과 표준편차

• 표본의 평균 = 표본평균(x̄, 엑스바)

  • 다른 알파벳 사용해도 됨
    • x를 가장 많이 사용
  • x̄ = (ΣX)/N
    → 표본의 데이터를 다 더해서 표본 개수로 나눔

• 표본의 표준편차 = 표본표준편차(s, 에스)

• 표본수치

  • 표본에서 구한 표본평균과 표본표준편차
    즉, x̄와 s

표준오차 vs 표준편차

• standard error & standard deviation
  

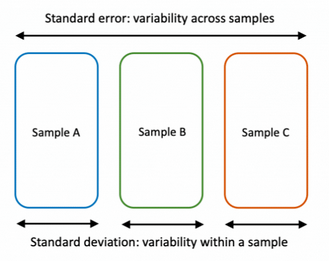
• 표준편차(Standard Deviation)

  • 표본 조사로 얻은 각 관측값과 표본평균의 차이를 나타낸다고 할 수 있음
  • 전국 성인 남녀의 몸무게를 조사하기 위해 1,000명을 랜덤으로 추출한다고 가정하면:
    • 모집단: 전국의 성인 남녀
    • 표본: 랜덤으로 추출된 1,000명의 성인 남녀
  • 표본의 크기가 1,000인 성인 남녀의 몸무게 평균을 62kg, 표준편차를 4.5kg이라 가정
    • Xᵢ를 표본조사를 통해 얻은 각 관측치라고 할 때 표준편차의 제곱:
      
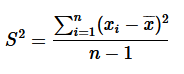
    • 모집단의 표준편차를 구할 때에는 분모에 n-1 대신 n으로 나누면 된다고 함

• 표준오차(Standard Error)

  • 표준편차를 표본크기의 제곱근으로 나눈 값
    
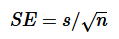
    • 표본의 크기(n)가 커질수록 표준오차의 값은 작아짐
  • 표본평균 추정값의 변동성을 의미
    • 표본 평균의 95% 신뢰구간을 구할 때:
      
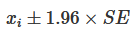
    • 표준오차가 작을수록 신뢰구간이 좁아지고, 표준오차가 커질수록 신뢰구간이 넓어짐
    • 따라서 표준오차가 작다는 것은 신뢰구간을 좁혀주고 표본 평균 추정값을 줄여줌

• 샘플링 오류를 줄이기 위해서는 모집단에서 여러 번 표본추출을 하여 여러 표본 그룹이 있어야 하지만 현실적인 이유로 불가능한 경우가 대다수

  • 대부분은 모집단에서 한 번의 표본추출을 하고 이 표본들이 모집단을 대표한다고 추정
    • 위에서 본 예시로 본다면 표준오차는 4.5/(1000)^(1/2) ≒ 1.423
    • 표본의 수가 충분히 크면 중심극한정리에 의해 표본평균은 정규분포를 따르므로 이를 통해 95% 신뢰구간을 구할 수 있음: [62 ± (1.96*1.423)]

자유도와 불편 분산

• 자유도(degree of freedom, df)

  • 주어진 데이터에서 자유롭게 변할 수 있는 독립적인 값의 수
  • 통계적 검정 및 추정 과정에서 매우 중요한 역할을 함
    • 데이터의 분산과 표준편차 계산할 때 특히 중요

• 자유도는 주로 다음과 같은 상황에서 사용:

  • 표본 분산과 표준편차 계산
    • 표본의 분산을 계산할 때 자유도는 표본의 크기(n)에서 1을 뺀 값으로 계산
    • 표본의 평균을 이미 계산하여 하나의 자유도를 잃었기 때문(n개의 데이터 포인트 중 하나는 이미 평균을 계산하는 데 사용되었기 때문에 실제로 자유롭게 변할 수 있는 데이터 포인트는 n−1개)
  • t-검정 및 f-검정
    • t-검정에서 자유도는 두 표본에서 각각 1을 뺀 값으로 계산
    • f-검정에서는 두 표본의 분산을 비교할 때 각각의 자유도를 사용
  • 회귀 분석
    • 회귀 분석에서 자유도는 데이터 포인트의 수에서 추정된 회귀 계수의 수를 뺀 값으로 계산
    • 단순 선형 회귀의 경우 데이터 포인트 수(n)에서 회귀 계수의 수(2: 절편과 기울기)를 뺀 값이 자유도

• 자유도 개념이 중요한 이유

  • 정확한 추정
  • 검정 통계량의 분포

• 불편 분산(unbiased variance)

  • 표본 분산(sample variance)를 구할 때 사용되는 개념으로 모집단 분산(populatopm variance)의 편향되지 않은 추정값을 제공하는 방법 → 이를 이해하기 위해 자유도의 개념을 사용

• 자유도와 불편 분산

  • 표본 분산을 계산할 때 표본 평균(sample mean)을 이용하는데, 이는 모집단의 평균을 추정한 값
  • 표본 평균을 사용하면 표본 내의 데이터 포인트 하나가 고정되기 때문에, 나머지 데이터 포인트는 자유롭게 변할 수 있는 상태가 되지 않음
  • 이러한 이유로 자유도는 표본의 크기(n)에서 1을 뺀 값이 됨

더 알고 싶으면 여기