지난 시간 복습
- RNN(순환신경망)
- Sequential data 학습 시 사용
- 인간의 기억 방식을 모방
- 일반신경망과 순환신경망의 차이
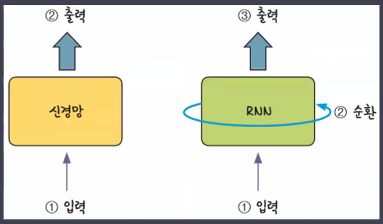
- "잠시 기억" == 기억가중치 → 기억가중치를 가지고 학습
- 앞에서 나온 입력에 대한 결과가 뒤에서 나오는 입력 값에 영향을 줌
- "오늘 주가가 몇이야?"에 대핸 일반 신경망은 '몇이야?' 만 고려
- 순환신경망은 이전 시점까지 고려(오늘, 주가)
- 순환신경망은 같은 층 안에서 맴도는 성질
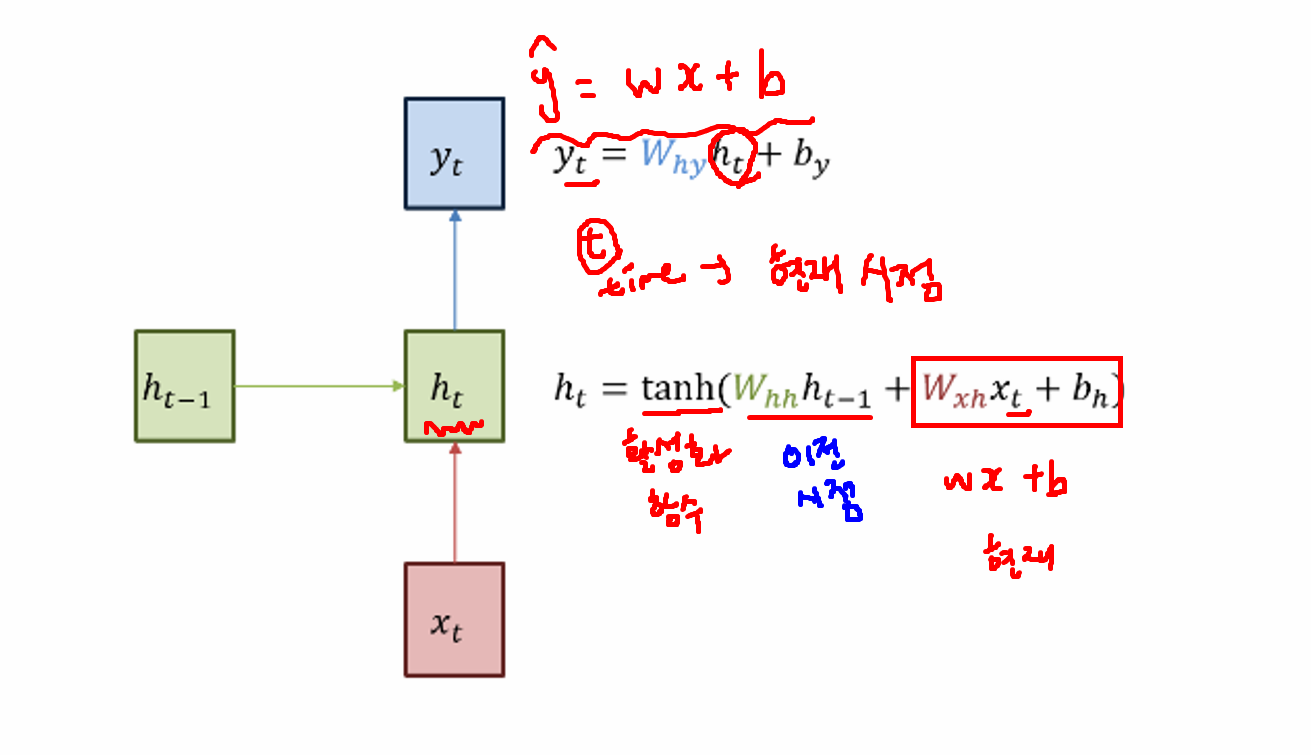
- 기본 구조
- one to many: 사진 설명(사진 → 단어들)
- many to one: 감정분석
- many to many: 기계번역
- SimpleRNN 실습

실습: 월별 항공 승객 수 예측
시각화
- 항공 승객 변화율 그래프 시각화
plt.figure(figsize=(12,6))
plt.plot(data["Month"], data[["#Passengers"]])
plt.show()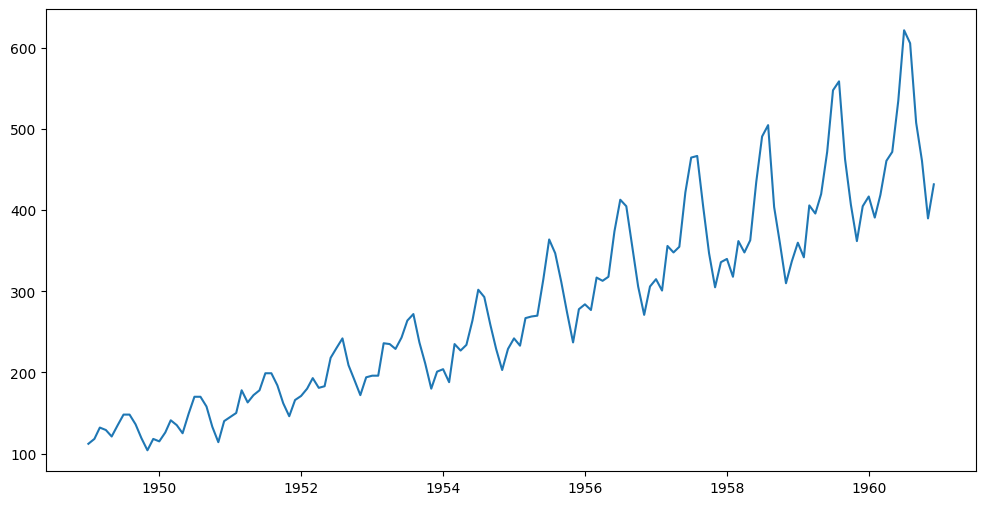
# 최근 2년 데이터 확인
df_recent=data.tail(24)
plt.figure(figsize=(10,3))
plt.grid()
plt.plot(df_recent["Month"], df_recent[["#Passengers"]])
plt.show()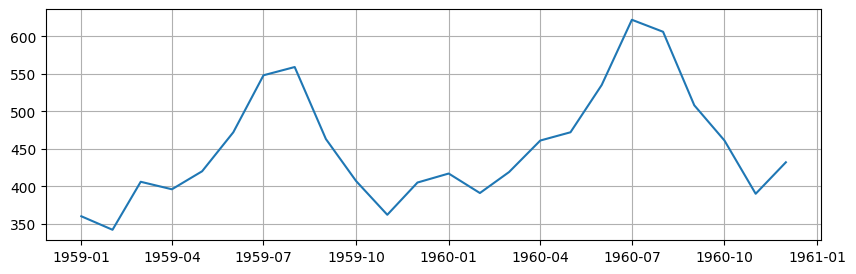
데이터 정규화
- RNN 모델링을 위한 데이터는 0~1 사이로 변환해주면 좋다
- 이미지 데이터, 센서 데이터도 0~1 사이로 변환
y = data[["#Passengers"]] # 2차원 구조로 추출해야 함(모델이 2차원만 받는다)
# MinMax스케일링
# RNN, 이미지 데이터에서 많이 활용
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
data_scale = scaler.fit_transform(y)데이터 분리
- 학습용, 검증용 분리
- 주의: train_test_split 사용하면 안 됨!
- 랜덤 샘플링 → 순서 섞어서 출력
- RNN은 시계열이 핵심 → 순서가 가장 중요한 특성이기 때문에 순서를 유지해야 함
- 주의: train_test_split 사용하면 안 됨!
# 데이터 길이를 기준으로 분할(8:2)
train_ratio = 0.8
train_size = int(len(data_scale)*train_ratio)
# (train) 학습용 데이터
train_data = data_scale[:train_size]
# 최근 1년 간의 데이터를 기반으로 예측
# 과거 기간을 얼마나 참조해서 예측할 것인지 지정해야 함
seq_length = 12
# (valid) 검증용 데이터
# 시계열 데이터의 예측은 과거 데이터를 기반으로 한다
# 시퀀스 연결을 위해 앞쪽에 seq_length 기간 포함해야 함
val_data = data_scale[train_size - seq_length:]
train_data.shape, val_data.shape((115, 1), (41, 1))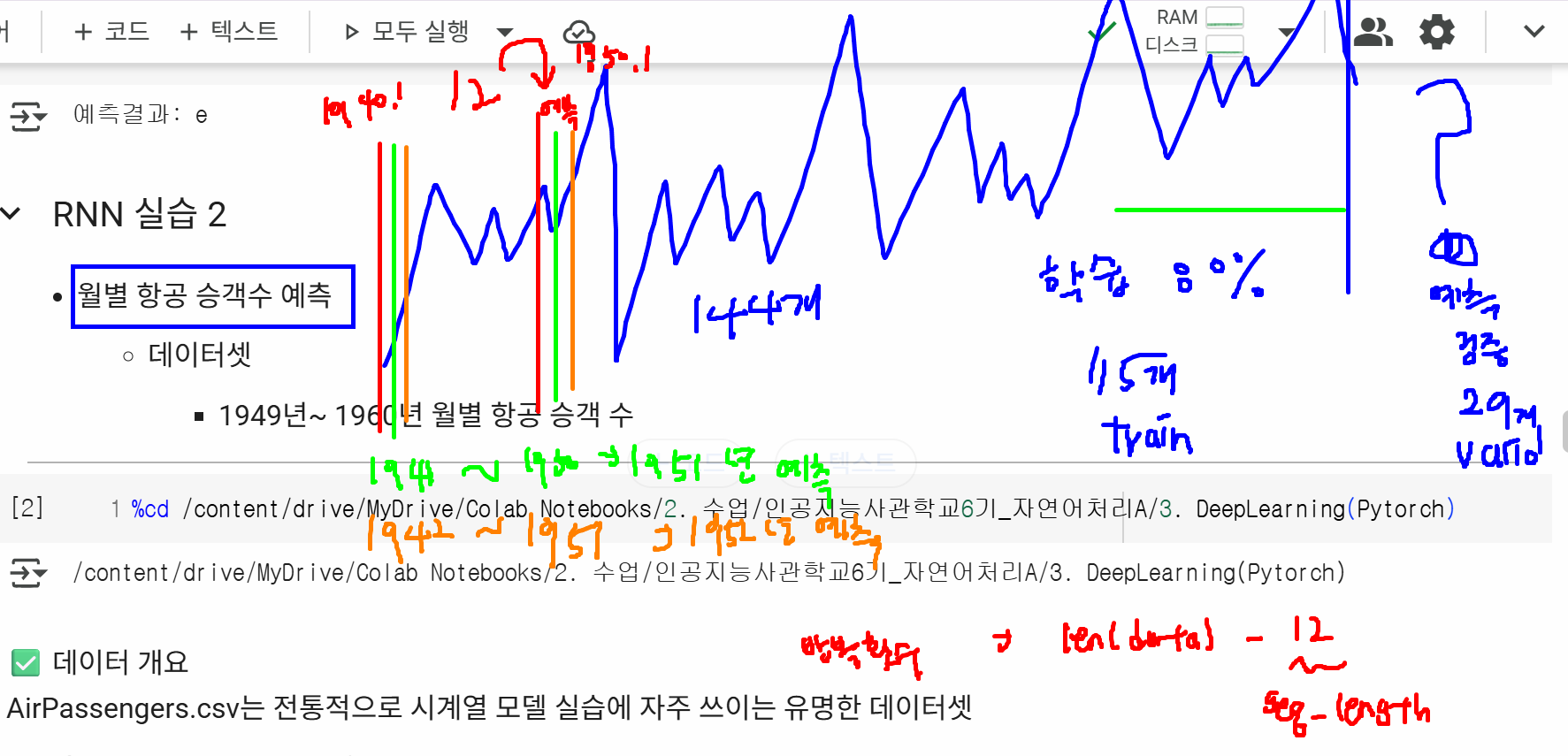
# 데이터(X: 입력 시퀀스, y: 정답값) → 쌍으로 묶어주자
# X: 이전 12개월의 항공 승객 수, y: 예측 승객 수
def create_seq (data, seq_length):
xs, ys = [], []
for i in range(len(data) - seq_length):
x = data[i:i+seq_length] # 입력 시퀀스 → 12개월 승객 수
y = data[i+seq_length] # 정답 시퀀스 →13번째 달 승객 수
xs.append(x)
ys.append(y)
return np.array(xs), np.array(ys) # 리스트를 넘파이 배열로 변환 (Tensor 변환을 위함)
X_train, y_train = create_seq(train_data, seq_length)
X_val, y_val = create_seq(val_data, seq_length)
# 데이터 텐서 변환
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32)
X_val_tensor = torch.tensor(X_val, dtype=torch.float32)
y_val_tensor = torch.tensor(y_val, dtype=torch.float32)
X_train_tensor.shape, y_train_tensor.shape, X_val_tensor.shape, y_val_tensor.shape(torch.Size([103, 12, 1]),
torch.Size([103, 1]),
torch.Size([29, 12, 1]),
torch.Size([29, 1]))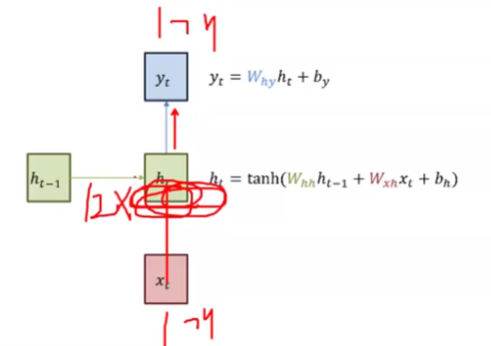
RNN 모델링
# RNN 모델 정의 → 회귀 모델
class RNN(nn.Module):
def __init__(self, input_size=1, hidden_size=32, output_size=1, num_layers=1):
super().__init__()
self.rnn = nn.RNN(input_size=input_size, hidden_size=hidden_size, batch_first=True, num_layers=num_layers)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self,x):
output, h_n = self.rnn(x) # out: 각 time step의 hidden state를 모두 포함(매 시퀀스마다 나오는 값), h_n: 최종 시퀀스의 전체 값(마지막 레이어의 최종 hidden state를 의미)
out = self.fc(output[:,-1])
# 마지막 시점만 사용하겠다는 의미 ← h_m은 num_layers가 많아지면 그걸 다 가지고 옴: squeeze를 쓸 수 없음(dim이 1이 아니게 됨)
# 따라서 h_n.squeeze 아닌 out[:,-1] 사용
return out
# 모델 하이퍼파라미터들 설정 → 객체 생성
model = RNN(input_size=1, hidden_size=32, output_size=1, num_layers=1)
loss_func = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
# 학습에 필요한 변수 설정
n_epochs=100
h1=[]
for epoch in range(n_epochs):
# 학습
y_pred = model(X_train_tensor)
loss = loss_func(y_pred, y_train_tensor)
optimizer.zero_grad()
loss.backward()
optimizer.step() # 가중치 업데이트
h1.append(loss.item())
# 검증
with torch.no_grad():
y_pred = model(X_val_tensor)
val_loss = loss_func(y_pred, y_val_tensor)
# 100회 학습 중 10회 단위로 출력
if (epoch+1) % 10 == 0:
print(f"Epoch: {epoch+1} | train loss: {loss.item():.4f} | val loss: {val_loss.item():.4f}")Epoch: 10 | train loss: 0.0196 | val loss: 0.0720
Epoch: 20 | train loss: 0.0112 | val loss: 0.0284
Epoch: 30 | train loss: 0.0071 | val loss: 0.0168
Epoch: 40 | train loss: 0.0052 | val loss: 0.0157
Epoch: 50 | train loss: 0.0044 | val loss: 0.0143
Epoch: 60 | train loss: 0.0040 | val loss: 0.0130
Epoch: 70 | train loss: 0.0037 | val loss: 0.0121
Epoch: 80 | train loss: 0.0033 | val loss: 0.0110
Epoch: 90 | train loss: 0.0029 | val loss: 0.0093
Epoch: 100 | train loss: 0.0024 | val loss: 0.0079# 시각화
plt.figure(figsize = (10,3))
plt.plot(h1)
plt.show()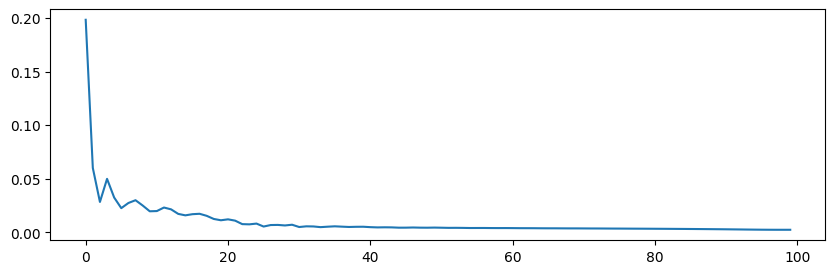
# 그래프: 실제 데이터 변화, 예측 데이터 변화
y_pred_val = scaler.inverse_transform(y_pred.numpy())
y_val = scaler.inverse_transform(y_val_tensor.numpy())
# 월 인덱스 생성
val_date = data["Month"][train_size:].reset_index(drop=True)
plt.subplots(figsize=(12,5))
plt.plot(val_date, y_val, label="actual")
plt.plot(val_date, y_pred_val, label="prediction")
plt.legend()
plt.show()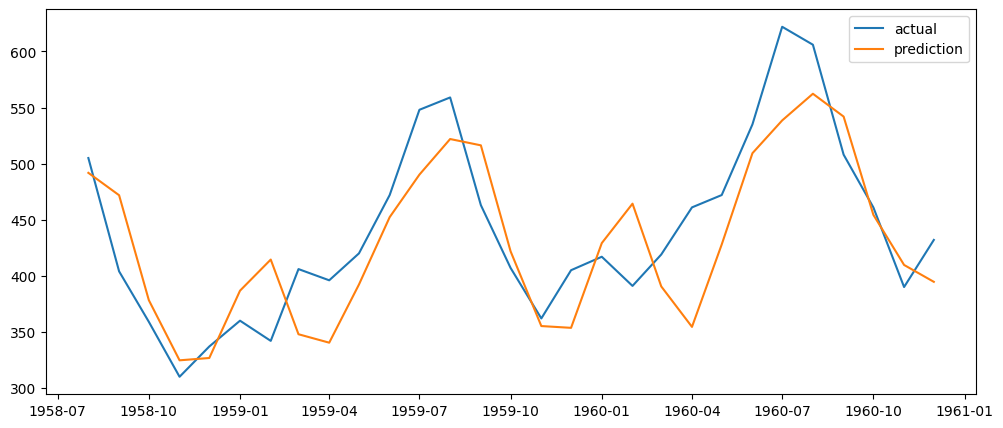
추가: PyTorch RNN 모델의 출력값
-
PyTorch RNN 모델의 출력값은 입력 시퀀스의 각 시점에 대한 hidden state와 마지막 시점의 output 을 포함합니다.
-
출력값은 일반적으로 텐서 형태로 제공되며, 배치 크기, 시퀀스 길이, hidden state 크기 등의 차원을 가집니다.
-
자세한 설명:
- PyTorch에서 RNN 모델(nn.RNN, nn.LSTM, nn.GRU 등)을 사용하면 입력 시퀀스의 각 time step에 대한 hidden state와 최종 hidden state를 얻을 수 있습니다.
- 이 출력값들은 텐서 형태로 제공되며, 다음과 같은 차원을 갖습니다.
- output:
(seq_len, batch, num_directions * hidden_size)
또는(batch, seq_len, num_directions * hidden_size)- seq_len: 입력 시퀀스의 길이입니다.
- batch: 배치 크기입니다.
- num_directions: RNN의 방향 (단방향 또는 양방향)에 따라 1 또는 2입니다.
- hidden_size: 각 time step에서 hidden state의 크기입니다.
- hidden:
(num_layers * num_directions, batch, hidden_size)- num_layers: RNN 레이어의 개수입니다.
- num_directions: RNN의 방향 (단방향 또는 양방향)에 따라 1 또는 2입니다.
- batch: 배치 크기입니다.
- hidden_size: 각 time step에서 hidden state의 크기입니다.
-
예시:
import torch
import torch.nn as nn
# RNN 모델 정의
rnn = nn.RNN(
input_size=10
, hidden_size=20
, num_layers=2
, batch_first=True
)
# 입력 데이터 (예시)
inputs = torch.randn(5, 3, 10)
# (batch, seq_len, input_size)
# 초기 hidden state (선택 사항)
h0 = torch.randn(2, 5, 20)
# (num_layers * num_directions, batch, hidden_size)
# 출력 및 마지막 hidden state 계산
output, hn = rnn(inputs, h0)
# 출력 및 hidden state shape 확인
print("Output shape:", output.shape)
print("Hidden state shape:", hn.shape)위 예시에서 output은 (5, 3, 20)의 shape을 가지며, 이는 배치 크기 5, 시퀀스 길이 3, hidden size 20을 의미합니다. hn은 (2, 5, 20)의 shape을 가지며, 2개의 레이어, 배치 크기 5, hidden size 20을 나타냅니다.
- 추가 정보:
- batch_first=True: 입력 데이터의 shape을 (batch, seq_len, input_size)로 지정합니다. 기본값은 (seq_len, batch, input_size)입니다.
- num_layers: RNN 레이어의 수를 지정합니다.
- num_directions: RNN의 방향 (단방향 또는 양방향)을 지정합니다.
마지막 hidden state (hn): 마지막 레이어의 최종 hidden state를 의미합니다. 필요에 따라 초기 hidden state를 지정할 수 있습니다. - 출력 (output): 각 time step의 hidden state를 모두 포함합니다. 분류 문제에서는 일반적으로 마지막 time step의 hidden state를 사용합니다. 시계열 예측 문제에서는 모든 time step의 hidden state를 사용할 수 있습니다.
LSTM (Long Short Term Memory)
- LSTM: RNN의 문제점을 극복하기 위한 대안
- Long Short Term Memory
- 순환 횟수가 많더라도 앞에서 연산한 결과를 장기간 유지할 수 있는 '구조'가 필요 → RNN에 메모리 셀(cell) 추가
- 메모리 셀(cell)
- 시각 t에서 메모리 셀의 c에는 과거로부터 현재 시각 t까지 필요한 대부분의 정보가 저장
- 오차역전파 시 tanh와 같은 활성화 함수를 통과하지 않아 기울기 소실이 일어나지 않음
- 데이터를 LSTM 계층 내에서만 주고 받으며 다른 계층으로는 전달하지 않음
- RNN 모델의 기억 소실 문제를 보완한 모델
- Simple RNN의 문제점: 장기 의존성 문제(Long-Term Dependency)
- 활성화 함수로 tanh()를 사용하기 때문에 timesteps(순환 횟수)가 길어질수록 역전파 시 기울기가 점차 줄어 학습 능력이 저하됨 → 기울기 소실 문제(Vanishing Gradient) 발생: 시간이 지나면 이전의 입력값을 잊어버리게 된다!
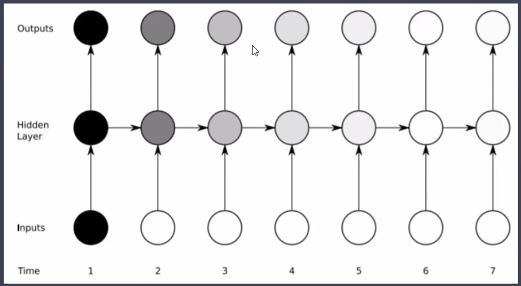
- 순환 횟수가 길어질수록 초반에 입력된 단어의 기억 데이터가 소실되는 기울기 소실 현상이 발생
- 시계열 데이터 중 초반 데이터가 후반 예측에 영향을 주는 경우 기본 RNN은 학습 성능이 낮다
- 활성화 함수로 tanh()를 사용하기 때문에 timesteps(순환 횟수)가 길어질수록 역전파 시 기울기가 점차 줄어 학습 능력이 저하됨 → 기울기 소실 문제(Vanishing Gradient) 발생: 시간이 지나면 이전의 입력값을 잊어버리게 된다!
- 문제 예시
- 어제 저녁 하늘에는 반짝이는 보석 같이 아름다운 ___ 가(이) 있었다 → 별
- 장기기억이 없을 경우:
반짝이는 보석 같이 아름다운 ____가(이) 있었다 → 케이크, 황금, 별, 건물. …
- Simple RNN의 문제점: 장기 의존성 문제(Long-Term Dependency)
- 장기 기억, 단기 기억을 관리하는 계산이 추가된 모델
- 메모리셀 연산이 추가된 모델: 값의 중요도에 따라 가중치를 부여
- 연상량이 대폭 증가 → 연산 시간이 오래 걸림 → 보완: GRU 모델 (연산의 속도 개선)
# LSTM 모델 설계 → 내부적으로 연산이 추가된 거라 설계 방식은 기존과 동일함
class LSTM(nn.Module):
def __init__(self, input_size, hidden_size, num_layers, output_size):
super(LSTM, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.num_layers = num_layers
self.istm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
output, _ = self.istm(x) # 사용하지 않을 변수일 경우 이름을 그냥 '_'로 줌
out = self.fc(output[:,-1])
return out
# 객체 생성
model_lstm = LSTM(input_size=1, hidden_size=32, num_layers=1, output_size=1)
# 손실 함수, 최적화 함수 설정
loss_func = nn.MSELoss()
optimizer = torch.optim.Adam(model_lstm.parameters(), lr=0.01)
n_epochs=100
print_interval=10
h1=[]
for epoch in range(n_epochs):
# 학습
y_hat = model_lstm(X_train_tensor)
loss = loss_func(y_hat, y_train_tensor)
optimizer.zero_grad()
loss.backward()
optimizer.step()
h1.append(loss.item()) # 학슴이 잘 되었는지(=loss가 감소했는지) 그래프를 그려 확인하기 위
# 검증
with torch.no_grad():
y_hat = model_lstm(X_val_tensor)
val_loss = loss_func(y_hat, y_val_tensor)
if (epoch+1) % print_interval == 0:
print(f"Epoch: {epoch+1} | train loss: {loss.item():.4f} | val loss: {val_loss.item():.4f}")Epoch: 10 | train loss: 0.0205 | val loss: 0.0873
Epoch: 20 | train loss: 0.0091 | val loss: 0.0565
Epoch: 30 | train loss: 0.0065 | val loss: 0.0207
Epoch: 40 | train loss: 0.0054 | val loss: 0.0206
Epoch: 50 | train loss: 0.0048 | val loss: 0.0171
Epoch: 60 | train loss: 0.0045 | val loss: 0.0164
Epoch: 70 | train loss: 0.0041 | val loss: 0.0141
Epoch: 80 | train loss: 0.0032 | val loss: 0.0114
Epoch: 90 | train loss: 0.0028 | val loss: 0.0097
Epoch: 100 | train loss: 0.0023 | val loss: 0.0101# 시각화
plt.figure(figsize = (10,3))
plt.plot(h1)
plt.show()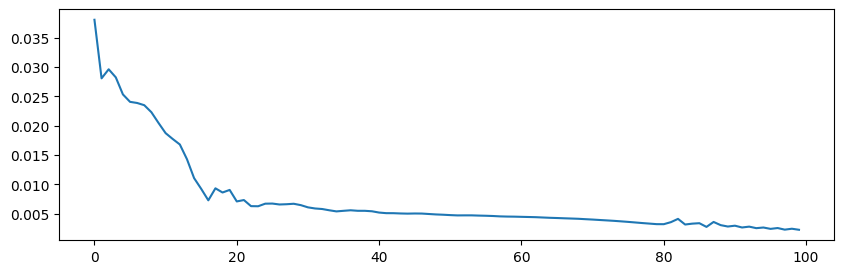
y_hat_val = scaler.inverse_transform(y_hat.detach().numpy())
y_val = scaler.inverse_transform(y_val_tensor.numpy())
val_date = data["Month"][train_size:].reset_index(drop=True)
plt.subplots(figsize=(12,5))
plt.plot(val_date, y_val, label="actual")
plt.plot(val_date, y_pred_val, label="prediction")
plt.legend()
plt.show()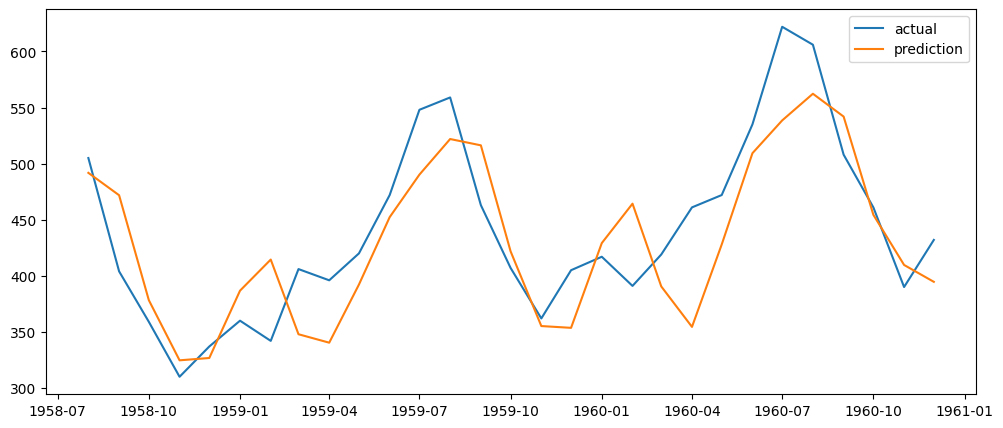
LSTM의 구조
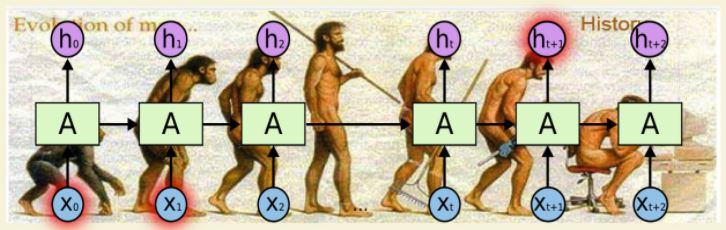
- RNN 구조
- 모든 RNN은 Neural Network 모듈을 반복시키는 체인과 같은 형태
- SimpleRNN은 아래와 같이 반복되는 간단한 구조를 가짐
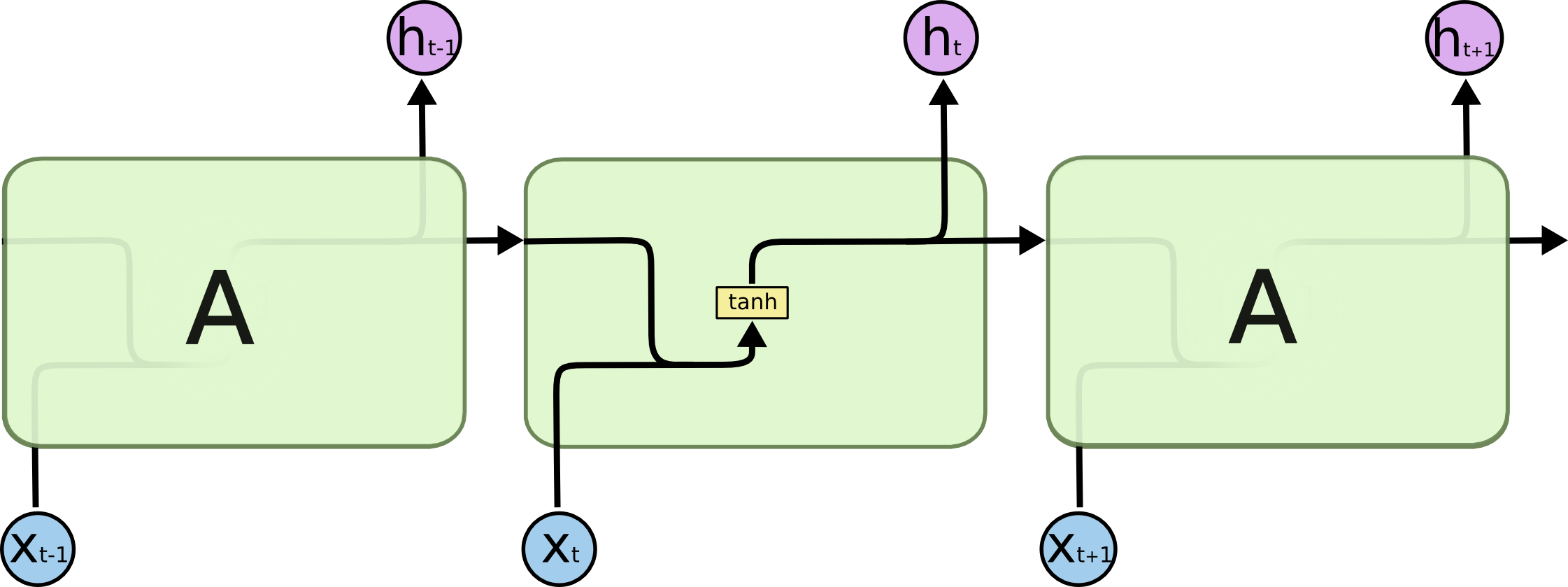
- LSTM 구조
- LSTM도 똑같이 체인 구조를 가지고 있지만, 4개의 Layer가 특별한 방식으로 서로 정보를 주고받도록 설계됨
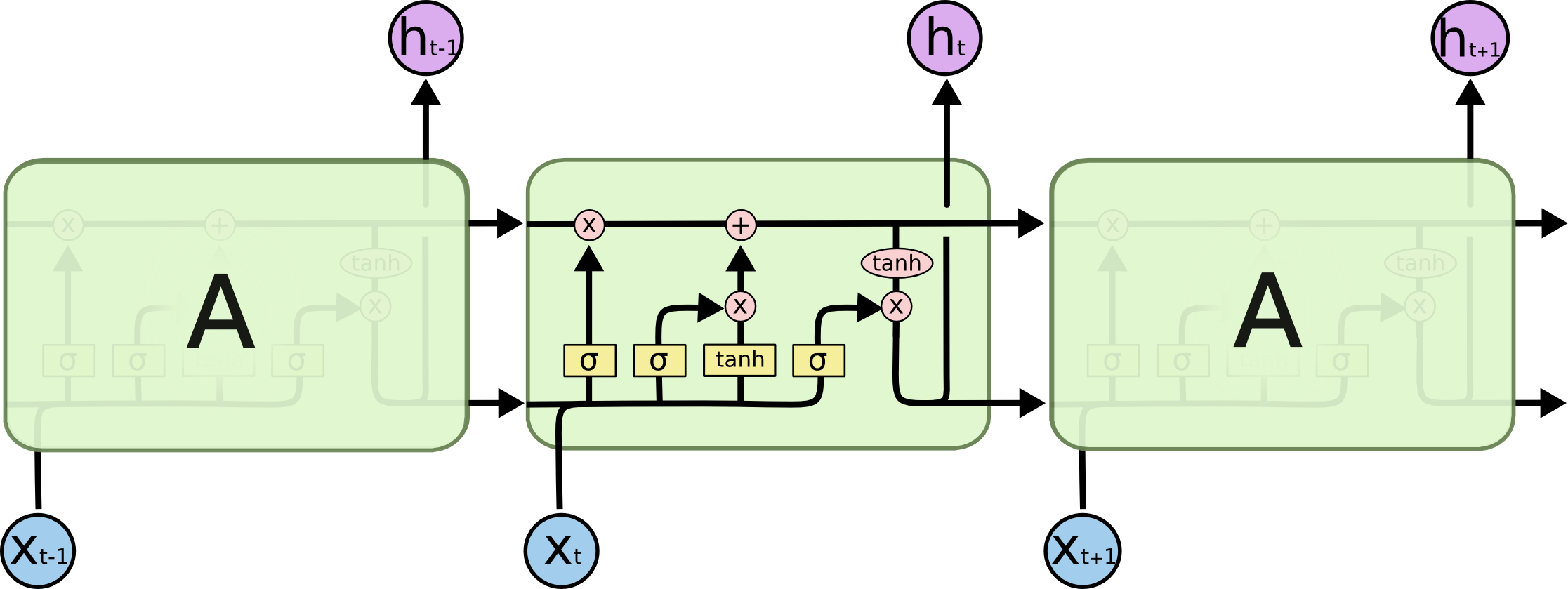
- LSTM도 똑같이 체인 구조를 가지고 있지만, 4개의 Layer가 특별한 방식으로 서로 정보를 주고받도록 설계됨
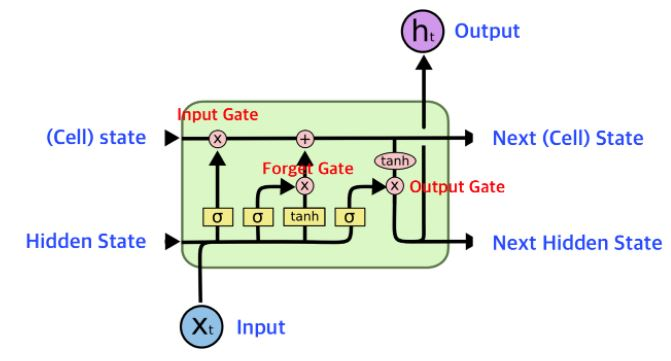
- LSTM 1개는 3개의 gates로 구성
- forget gate
- 이전 상태 정보를 얼마나 버리고 얼마만큼을 저장할지 결정
- input gate
- 입력되는 새로운 정보를 얼마만큼 저장할지 결정
- output gate
- 현재 LSTM 셀의 어떤 부분을 다음 LSTM 셀로 전달할지 결정
- forget gate
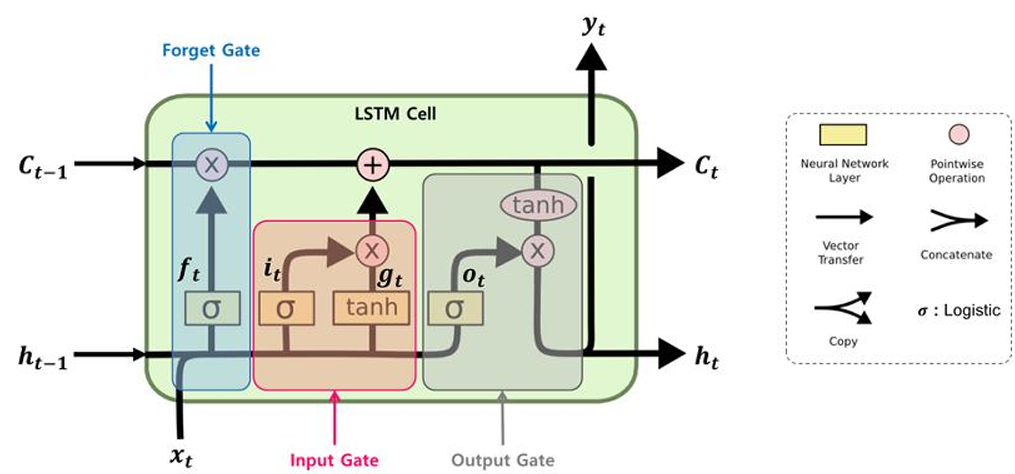
- h: 단기 상태(Short-Term state)
- C: 장기 상태(Long-Term state)
- 이전 스텝의 장기 기억 은 왼쪽에서 오른쪽으로 통과하면서 Forget gate를 지남 → 일부 정보를 잃고(sigmoid가 곱해지기 때문), Input gate로부터 덧셈(+) 연산을 통해 새로운 정보를 추가하여 현재 타임 스텝의 장기 기억 가 생성됨
- 는 Output gate의 tanh 함수로 전달되어 단기 상태 를 만듦
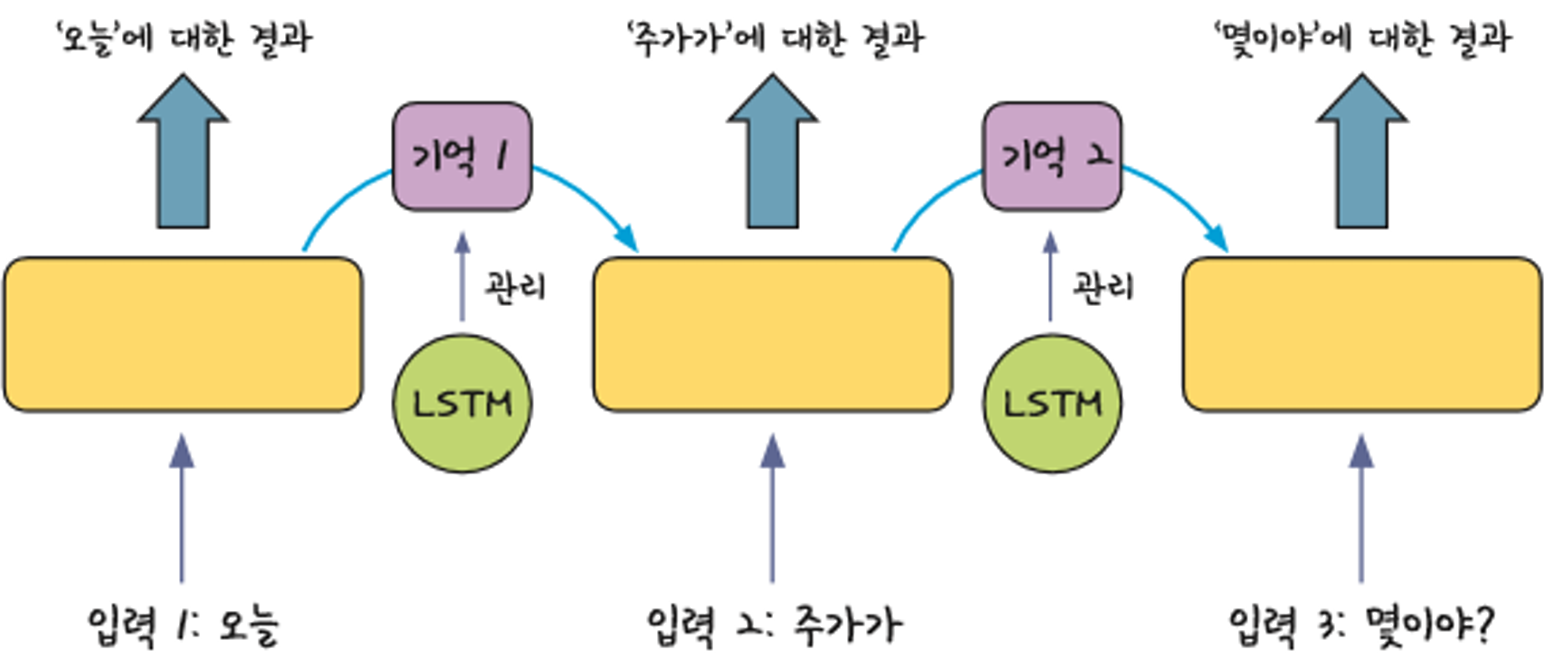
- LSTM은 총 6개의 파라미터와 4개의 게이트를 가짐
하루 돌아보기
👍 잘한 점
- 과제 당일 제출 완료
- AI PLUS IN GWANGJU 컨퍼런스 끝까지 집중해서 잘 들었음
- 매우 유익한 시간이었다.
👎 아쉬웠던 점
- 정보처리기사 시험 준비가 생각보다 더 안 되고 있음
🔬 개선점
- 다음 주부터는 진짜 정보처리기사 시험 공부에만 집중하기
