머신 러닝 특강: 군집 분석

Suhyeon Lee·2024년 11월 28일
라이브 세션
0

라이브 세션

목록 보기
30/37

목표

  • 클러스터링(Clustering) 개념 이해
  • 클러스터링 프로세스 숙지
  • 데이터 분석가가 클러스터링을 통해 얻을 수 있는 인사이트 이해
  • 코드를 통한 학습

→ 머신 러닝 중 비지도 학습에 해당하는 군집화와 차원 축소에 대한 내용



클러스터링이란?

정답이 없을 때, 정답을 찾아가는 과정

클러스터링 = 군집분석

  • 데이터 분석에서 피쳐(컬럼) 유사성의 개념을 기반으로 전체 데이터셋을 그룹으로 나누는 그룹핑 기법

    • 각 그룹을 클러스터라고 함

  • 현업에서는 kaggle dataset 과는 다르게, 방대한 DB가 구축되어 있음

    • 데이터 분석가는 이러한 데이터 속에서 의미 있는 특징(컬럼)을 찾고, 최적의 그룹 게수를 찾아 그룹별 인사이트를 도출해내는 역할을 수행



클러스터링 프로세스

러프한 프로세스 살펴보기

pre-processing

1. 기간 선정

  • 클러스터링을 위한 데이터 기간을 설정
    • 의미 있는 패턴을 도출하기 위해서는 최소 3개월 이상의 데이터셋이 권장
    • 회사가 의도하는 목적에 따라서 유연하게 변경될 수 있음
  • 클러스터링의 목적은 live한 데이터의 유입 시 해당 유저의 행동을 통해, 이를 알맞게 배치시키는 모델의 생성
    • 해당 모델은 초기에 생성되고, 서비스 변동사항에 따라서 일정 주기에 따라 재시행됨

2. 이상치 기준 선정 및 제외

  • IQR, Z-SCORE 등 다양한 이상치 기법을 사용해보고, 이상치 비중을 기록
    • 이 역시 통계적 기법이 사용될 수도 있겠으나 회사의 니즈에 따라 특정 조건에 따라 이상치의 기준을 정립하고 이를 적용하여 데이터 핸들링을 진행하기도 함

다양한 이상치 기법에 각 기업에서만 적용하는 특별한 이상치 기준을 추가해줘야 해요!
예: 특정 아이피기 짧은 시간에 수백만 번 접속한 경우 소개한 이상치 기법으로 분류가 안 될 수 있음 → 이상치 기준 추가로 정해 따로 분리해야 함
단순히 기법만 사용하는 게 아니라 AND 조건으로 이상치를 까다롭게 처리해야 함
→ 정상인 유저를 이상한 유저라고 판단하면 절대 안 되기 때문!
★ AND 조건을 이용해 이상치를 까다롭게 분류해주세요 제발~ ★
e.g. z-score가 -3부터 3 범위를 벗어나고 ip 주소가 너무 많은 유저

Z-score

Z=x−μσμ=meanσ=standard deviationZ = \frac{x-\mu}{\sigma} \\\mu=mean \\\sigma=standard \ deviation
  • 데이터의 분포가 정규 분포를 이룰 때, 데이터의 표준 편차를 이용해 이상치를 탐지하는 방법
    • 각 데이터(행) 마다 Z-score 구하기
      • Z 값: X에서 평균을 뺀 데이터를 표준편차로 나눈 값. 표준 점수라고 부름.
  • 표준 점수는 평균으로부터 얼마나 멀리 떨어져 있는지를 보여주며, 일반적으로 -3에서 3 사이의 값을 가지고 있음
    • ±3 이상이면 이상치로 간주
  • Z-Score = 0
    • 해당 데이터는 평균과 같음을 의미(=평균에서 떨어진 거리가 0)
  • Z-Score > 0
    • 해당 데이터는 평균보다 큼
    • Z-Score가 1이면, 해당 데이터 포인트는 평균보다 1 표준편차만큼 더 큰 값임을 의미
  • Z-Score > 0
    • 해당 데이터는 평균보다 작음
    • Z-Score가 -1이면, 해당 데이터 포인트는 평균보다 1 표준편차만큼 더 작음을 의미

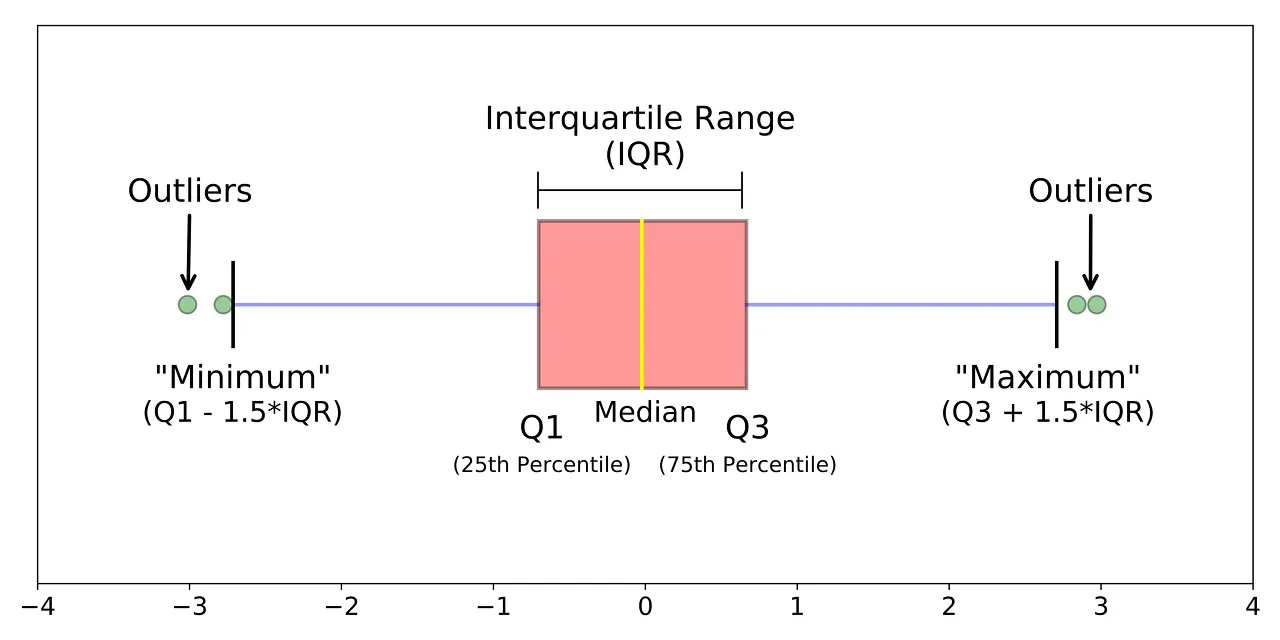
IQR(Interquartile Range)

  • 데이터의 분포가 정규 분포를 이루지 않을 때 사용
  • 데이터의 25% 지점(Q1Q_1)과 75% 지점(Q3Q_3) 사이의 범위(IQR)를 사용
    • 이를 벗어나는 값들은 모두 이상치로 간주
  • 이를 그림으로 그린 것이 Box Plot
    • IQR 밖의 데이터 포인트는 이상치로 표시됩니다.
    • IQR : (제 3사분위 값) - (제 1사분위 값)

Isolation Forest

  • 머신러닝 기법 중 하나
  • 컬럼 갯수가 많을 때 이상치를 판별하기 용이
  • 데이터셋을 결정트리 형태로 표현합니다.
  • 결정트리는 아래와 같은 형태
    • 질문에 질문들이 꼬리를 물고 이어져 각 값이 매, 펭귄, 돌고래, 곰 중 하나에 배치됨
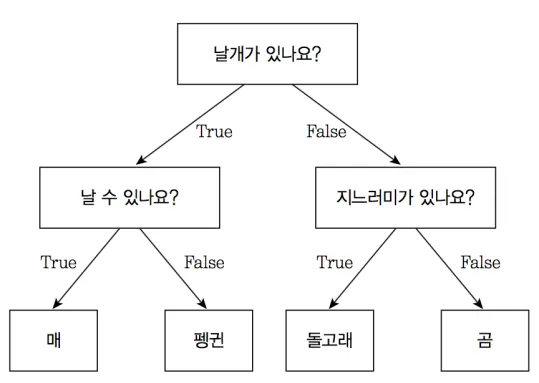
    • 하지만 이상치의 경우, 이 어디에도 속하지 않을 확률이 높아 구분되지 않겠죠?
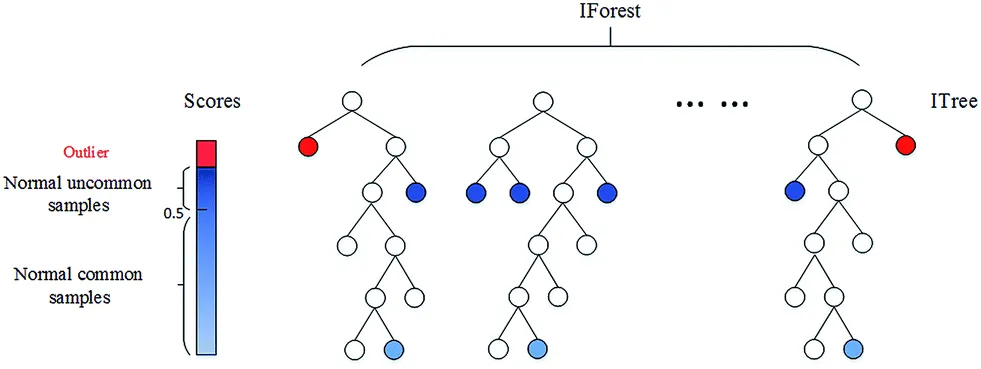
  • 한 번 분리될 때마다 경로 길이가 부여되며, 트리에서 몇 번을 분리해야 하는지(데이터까지의 경로 길이)를 기준으로 데이터가 이상치인지 아닌지를 판단
    • 즉 이상치는 다른 관측치에 비해 짧은 경로 길이를 가진 데이터
    • 경로 길이로 점수는 0 에서 1 사이로 산출되며, 결과가 1에 가까울수록 이상치로 간주

DBScan

  • 밀도 기반의 클러스터링 알고리즘
  • 어떠한 클러스터에도 포함되지 않는 데이터를 이상치(noise; outlier)로 탐지하는 방법
    • 복잡한 구조의 데이터에서 이상치를 판별하는 데 유용
    • 주로 지리 데이터 분석, 이미지 데이터 분석의 이상치 기법으로 사용
  • 각 데이터의 밀도를 기반으로 군집을 형성시키고, 설정된 거리 내에 설정된 최소 개수의 다른 포인트가 있을 경우, 해당 포인트는 핵심 포인트로 간주
  • 핵심 포인트들이 서로 연결되어 군집을 형성하며, 이와 연결되지 않은 포인트는 이상치로 분류

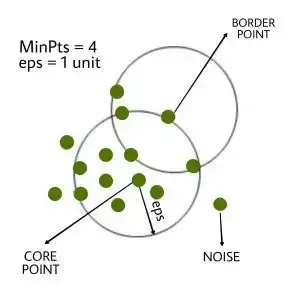
🡆 이상치는 머신 러닝 학습에 필요 없으니 그냥 drop해 주세요!

3. 표준화

  • 데이터의 크기가 너무 크거나, 컬럼 간 데이터 range 에 차이가 많을 때 일부 컬럼에 대해 진행
  • 대표적으로 두 가지를 많이 사용: minmax scale, standard scale

→ 원본 데이터가 가지고 있는 분포를 가지고 가야 해서 minmax는 안 씀

※ 표준화는 필수가 아님 ※
하지만 누가 봐도 표준화를 해야겠다는 컬럼(e.g. 혼자 단위가 엄청 큼)이 있을 수 있으니까 알아두세요~
추천 방식
① 표준화를 안 하고 돌려본다
② 표준화를 하고 돌려본다
③ 둘을 비교한다
④ PROFIT!

minmax scale

  • 모든 데이터의 값을 0과 1 사이에 배치
  • 이상치에 약하다는 특징을 가짐
  • 예시를 통해 살펴보기
    • df[’pay_amt’] = 0,0,0,0,1,2,3,100과 같은 값이 있다고 가정
      • 100 이 1에 배치되면서 나머지 값들은 0에 수렴하는 값을 가지게 되므로, 전체 데이터 분포가 뭉개지는 의미에서 이상치에 약하게 되는 것!

🡆 표준화보다는 정규화에 가까워요!
🡆 잘 사용하지 않아요!
(데이터 분포를 가져갈 수 없기 때문에 클러스터링에서는 아예 사용 안 함)

Min-Max Scaling은 모든 피처가 정확하게 [0,1] 사이에 위치하도록 데이터를 변경한다. 2차원 데이터셋일 경우에는 모든 데이터가 x축의 0과 1, y축의 0과 1 사이의 사각 영역에 담기게 된다.
Min-Max Scaling은 다음과 같은 공식으로 구할 수 있다: x′=x−xminxmax−xminx'=\frac{x-x_{min}}{x_{max}-x_{min}}
즉, 데이터에서 최솟값을 빼고 전체 범위로 나누는 것이다.
그래서 정규화=Min-Max Scaling인가? 사실 많은 인터넷 자료에서 두 개를 같은 개념으로 두고 보지만, Normalization ⊃ Min-Max Scaling이라는 표현이 더 맞을 것이다.
위에 유클리디안 거리로 계산하는 방법은 scikit-learn의 Normalizer로 구현 가능하다.

standard scale

  • 평균을 0, 표준편차를 1로 변환
    • minmax scale 이 가지는 한계점을 보완
  • standard scale 을 통해 각각의 data point 가 ‘평균으로부터 얼마나 떨어져 있는지’ 에 대한 수치로 변환
  • 군집분석 시 가장 많이 쓰이는 표준화 기법

🡆 표준화에 가까워요!
🡆 원래 데이터가 가지고 있는 분포를 그대로 가지고 가기 때문에 많이 사용해요! → 표준 정규 분포 따라가게 되는 거랑 같은 이치

클러스터링에서 표준화는 필수가 아닙니다!
둘 다 해보고 비교해봐야 해요
→ 표준화를 해서 클러스터링 결과가 더 좋을 수도 있고, 표준화를 하지 않았을 때 클러스터링 결과가 더 좋을 수도 있기 때문

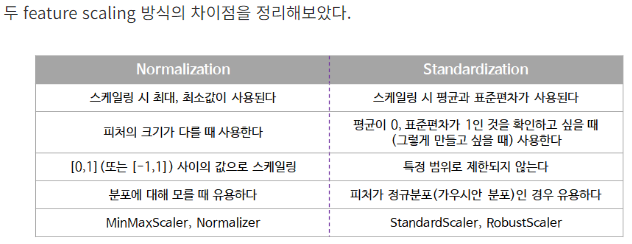
표준화와 정규화의 차이를 모르겠어요!
더 알아보기

  • 표준화(Standardization)
    • 표준화 또는 Z-score 정규화는 표준정규분포의 속성(μ=0,σ=1\mu=0,\sigma=1)을 갖도록 피처가 재조정되는 것
    • 0 주위에 표준편차 1의 값으로 배치되도록 피처를 표준화하는 것은 다른 단위를 가진 측정값을 비교할 때 중요할 뿐만 아니라 많은 기계 학습 알고리즘의 일반적인 요구 사항임
  • 정규화(Normalization)
    • 목적
      • 데이터셋의 numerical value 범위의 차이를 왜곡하지 않고 공통 척도로 변경하는 것
    • 기계학습에서 모든 데이터셋이 정규화 될 필요는 없고, 피처의 범위가 다른 경우에만 필요
      • 정규화를 통해 피처 벡터의 유클리디안 길이가 1이 되도록 데이터 포인트를 조정함
      • 다른 말로 하면 지름이 1인 원(3차원이라면 구)에 데이터 포인트를 투영함
      • 즉, 각 데이터 포인트가 다른 비율로 스케일이 조정된다는 것
    • 이러한 정규화는 특성 벡터의 길이는 상관 없고 데이터의 방향만이 중요할 때 많이 사용
  • 정규화와 표준화 모두 경사 하강 알고리즘을 더 빠르게 동작할 수 있도록 도와주는 것
    • 언제 정규화를 하고 언제 표준화를 할까?
      • 명확한 답은 없지만 통상적으로는 표준화를 통해 이상치를 제거하고, 그 다음 데이터를 정규화 해 상대적 크기에 대한 영향력을 줄인 다음 분석을 시작
    • 예시
      • cluster analysis에서 특정 거리 측도를 기반으로 피처 간의 유사성을 비교하기 위해 표준화가 특히 중요할 수도 있음
      • 주성분 분석(Principal Component Analysis)은 보통 Min-Max Scaling보다 표준화를 선호(왜냐하면 분산을 극대화하는 성분에 관심이 있기 때문)
      • 이미지 프로세싱에서 정규화가 자주 사용되는데, pixel intensities를 특정 범위(RGB 색상 범위의 경우 0~255) 내에 맞추려면 정규화가 필요하기 때문
        🡆 대충 데이터를 표준화해서 나쁠 거 없다는 뜻

4. 차원 축소(PCA)

  • 많은 컬럼으로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성하는 것
    (컬럼이 너무 많기 때문에 학습이 어렵고 더 좋은 특징만 가지고 사용하겠다는 것)
  • PCA는 가장 대표적인 차원 축소 기법
    • 여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소
      (데이터의 분포를 가장 잘 표현하는 성분을 찾아주는 것)
  • PCA 기법의 핵심은 가장 높은 분산을 가지는 데이터의 축을 찾아 그 축으로 차원을 축소하는 것인데, 이 축을 주성분이라고 함


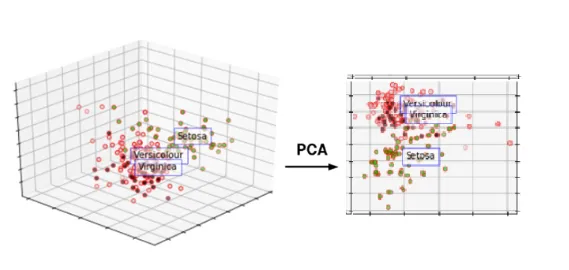
→ 데이터 분석가는 결제금액과 경험치를 동시에 보면서 또 다른 변수를 확인하고 싶음 🡆 PCA를 진행: 가장 높은 분산을 가지는 데이터의 축을 찾아 그 축으로 차원을 축소

→ 20개의 차원을 눈으로 볼 수 없음(3차원까지가 한계): 차원을 축소해 PC1, PC2 고름 → PCA plot

Experiment

5. K값(군집 게수), 초기 컬럼(피쳐) 선정

  • Silhouette Coefficient, elbow-point, Distance Map을 통해 초기 군집의 개수를 지정
    • 초기 컬럼의 설정은 모든 컬럼을 기준으로 진행
    • 클러스터링을 반복 진행하며, k값과 피쳐의 컨디션을 기록하고, 최적으로 구분된 컨디션을 찾게 됨
  • 경우에 따라서는 파생변수를 만들어 클러스터링을 진행하기도 함

Silhouette Coefficient

  • 실루엣 분석은 각 군집간의 거리가 얼마나 효율적으로 분리되어 있는지를 나타냄
    (효율적으로 잘 분리 되어있다 == 다른 군집과의 거리는 떨어져 있고, 동일 군집끼리 데이터는 서로 가깝게 뭉쳐있다는 의미)
  • 실루엣 계수는 -1에서 1사이의 값을 가지며, -1이나 1에 가까울수록 근처의 군집과 멀리 떨어져있는 것이며 0에 가까울수록 근처 군집과 가깝다는 뜻
    • 즉, -1 이나 1에 가까울수록 군집 간 거리가 유의미하게 구분된다는 것을 의미

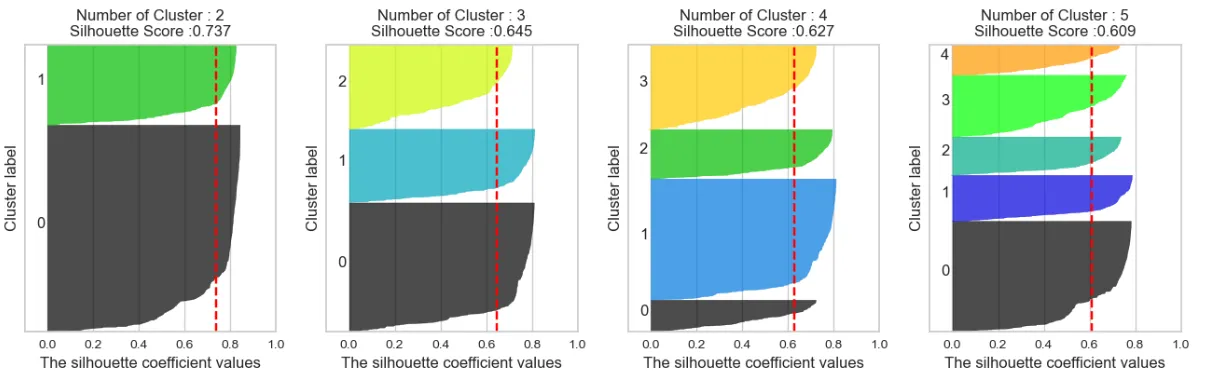
→ 점수가 제일 높으니까 2개로 해야지~ 🡆 절대 안 됨!
→ 해당 그래프는 어디까지나 참고용임
(백만 명을 두 그룹으로 나눈다? 말도 안 됨)

scree plot의 elbow-point

  • yellow brick library - elbow method를 사용하여, 알고리즘이 군집이 나뉘는 시간까지 고려한 k값을 도출

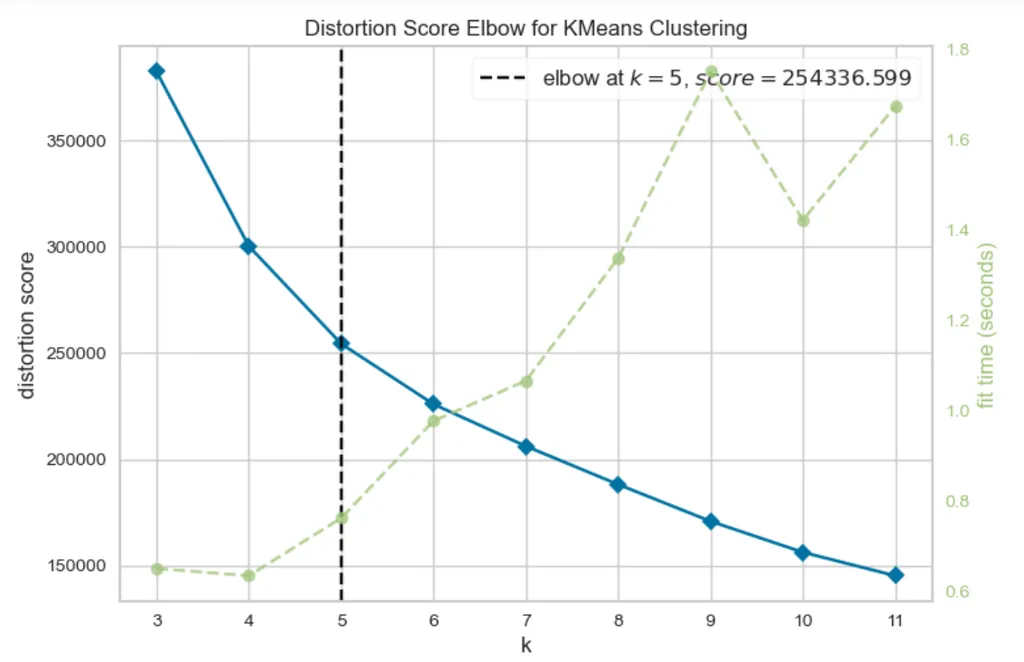
→ 어디까지나 참고로만 하는 것
→ elbow-point에서 "시작"임!
(elbow-point가 정답은 아님: 컬럼을 바꾸는 순간 k값도 달라지기 때문)

yellow brick library - elbow method가 가장 최근에 나온 scree plot이에요~

Distance Map

  • 군집 간 거리를 시각화 해주는 기법
  • 실행마다 다르게 보여질 수 있음
  • 군집이 떨어져 있는 거리를 가시적으로 확인하기 위한 참고치일 뿐이니, 이 점을 숙지할 것!

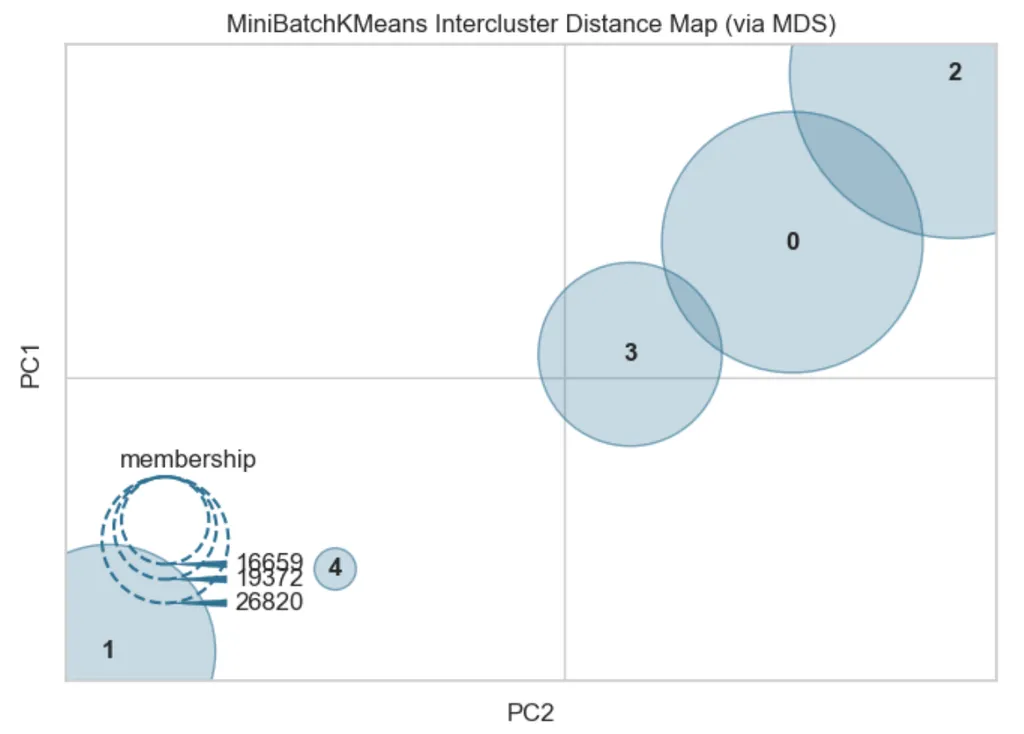
6. k-means clustering 시행

  • 데이터를 거리 기반 K개의 군집(Cluster)으로 묶는(Clusting) 알고리즘
    • K는 묶을 군집(클러스터)의 개수를 의미
    • means는 평균을 의미
  • 각 군집의 평균(mean)을 활용하여 K개의 군집으로 묶는다는 의미

알고리즘

  1. 군집 수 K 설정
  2. 초기 중심점 K개 설정
  3. 중심점을 기준으로 data point들의 거리를 비교하고, 더 가까운 중심점에 군집 할당
  4. 할당된 점들의 중심점 위치 조정됨
  5. 중심점의 위치가 변하지 않을 때까지 반복

k-means clustering 시행: 데이터를 거리기반 K개의 군집(Cluster)으로 묶는(Clusting) 알고리즘입니다. K-means 알고리즘에서 K는 묶을 군집(클러스터)의 개수를 의미하고 means는 평균을 의미해요. 각 군집의 평균(mean)을 활용하여 K개의 군집으로 묶는다는 의미입니다.

7. 군집 분포 확인

  • 데이터셋을 기반으로 데이터가 잘(얼마나 밀도있게) 나뉘었는지 확인하는 과정

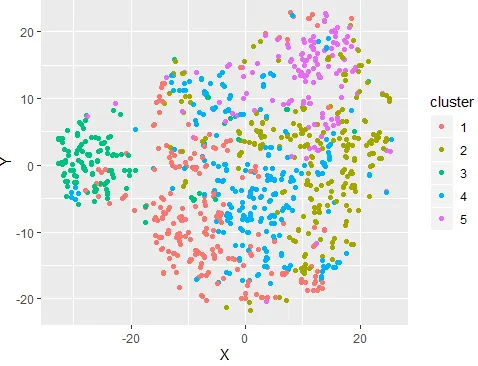
  • 위의 scatter plot은 군집이 잘 나뉘어지지 않은 것이 한눈에 보임
    • K값과 컬럼(피쳐)를 조정하며, 아래 scatter plot과 같이 군집별 특성이 명확하고, 각각의 data point가 충돌하지 않도록 실험을 반복해야 함

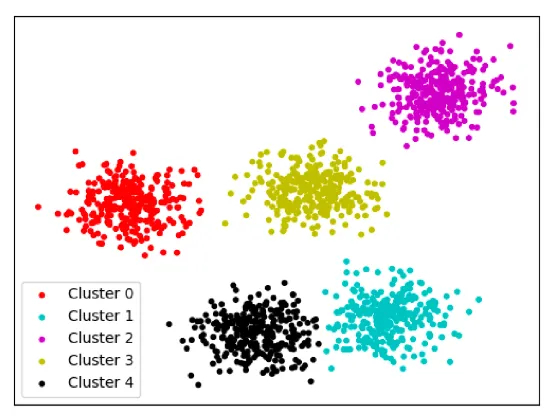
8. 2~7번 과정을 반복하며 최적의 결과 도출

  • 실험을 수행할 때마다, 다양한 기준을 고려해야 함
    • 통계학적인 지식을 필요로 하지만, 이 부분이 클러스터링의 모든 부분을 설명해 주지는 않음
    • 비지도 학습인 만큼, 데이터분석가의 주관이 개입되어야 함!

실험시 고려되어야 할 사항

  • 데이터 자체에 결측이 많은가?
  • 데이터가 결측은 아니나, value가 0인 경우가 많은가?
  • 데이터의 전반적인 분포는 어떠한가?
  • 컬럼 간 상관계수는 어떠한가?
  • 데이터가 불규칙한가?
  • 컬럼이 가지는 개념적인 의미는 무엇인가?
  • 컬럼값이 이진형인가?
  • cluster 비중이 지나치게 편향되어 있는가?

게임 유저 클러스터링인데 결제 금액을 뺐을 때 클러스터링이 잘 된다고 결제 금액 컬럼을 빼는 건 어불성설

9. 모델링

  • 클러스터링 결과를 가지고 이를 모델에 학습
    • 모델을 만드는 의의
      • 모델은 우리가 실험한 로직을 매번 수행하지 않도록 해주는 중요한 개념

10. 데이터 적재 및 자동화 설정

  • cluster 별로 나뉜 고객들을 별도 테이블에 저장
    • 모든 과정은 python 으로 진행될 수 있음
  • 스케줄 기능을 통해, 주기별로 라이브한 데이터를 자동 테이블 적재하는 것까지가 클러스터링의 최종 작업

11. 인사이트 도출

  • 적재된 테이블을 가지고 클러스터별로 인사이트를 도출할 수 있게 됨!


python code 실습

1. 라이브러리 import

# 기본 라이브러리 import 
import pandas as pd
import numpy as np
# 시각화 라이브러리 import 
import seaborn as sns
import matplotlib.pyplot as plt

# 표준화 라이브러리 import 
from sklearn.preprocessing import StandardScaler
# k 값 참고: scree plot을 통한 k 값 확인을 위한 라이브러리 import 
from yellowbrick.cluster import KElbowVisualizer
# k 값 참고: distance map 라이브러리 import 
from yellowbrick.cluster import intercluster_distance
from sklearn.cluster import MiniBatchKMeans
# k 값 참고: 실루엣 계수 확인을 위한 라이브러리 import 
from sklearn.metrics import silhouette_score
# 데이터셋 주성분 분석중 하나인 pca 를 수행하기 위한 라이브러리 import 
from sklearn.decomposition import PCA
# k-means 알고리즘 활용을 위한 라이브러리 import 
from sklearn.cluster import KMeans
import warnings 
warnings.filterwarnings('ignore')

2. 데이터 가져와 탐색(EDA)

# 데이터셋 로드
base_df = pd.read_csv('merge_df.csv')

# 결측치 확인
base_df.isnull().sum()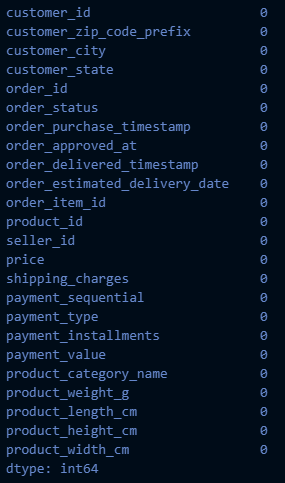

# 클러스터링 할 컬럼 지정
feature_names=['customer_zip_code_prefix','price','shipping_charges','payment_sequential','payment_value']

# 지정된 컬럼으로 새로운 dataframe 생성 
base_df = pd.DataFrame(base_df, columns=feature_names)

base_df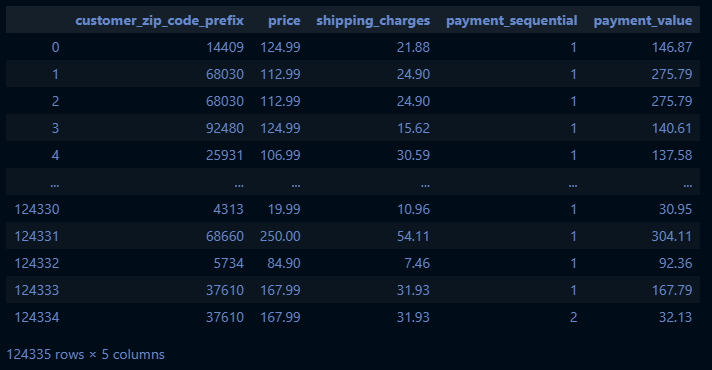

→ 고유값(e.g. zipcode)은 반드시 빼고 수치형 데이터만 가지고 와서 진행하세요!
→ feature를 가져올 때는 기본적으로 연속형 변수가 핵심
→ 경우에 따라서는 범주형 변수를 인코딩을 통해 수치형 변수로 만들 수도 있음
→ 이진형은 웬만하면 넣지 마세요

# 표준화
# 표준화 방식: standard scaler (평균0, 분산1)
scale_df = StandardScaler().fit_transform(base_df)

scale_df

→ 표준화는 컬럼 하나하나 넣어주는 거 아님!
한 번 넣어주면 알아서 컬럼끼리 수행함

# 주성분 개수를 판단하기 위한 pca 임의 시행 
pca = PCA(n_components=3)
pca.fit(scale_df)
# 설정한 주성분의 갸수로 전체 데이터 분산을 얼만큼 설명 가능한지 
pca.explained_variance_ratio_.sum()

→ n_components=3: 3차원으로 보겠다는 이야기임
→ 눈으로 보고 싶으면 2 또는 3 넣으면 됨!
(4 이상은 파이썬도 못 그리고(시각화 못하고) 우리도 못 그려요)

→ base_df의 컬럼 3개를 가져오는 게 아니라 그냥 성분을 3개로 한다는 것!

# pca 시행
pca_df = pca.fit_transform(scale_df)
pca_df = pd.DataFrame(data = pca_df, columns = ['PC1','PC2','PC3'])  

# Show the first 5 firms
pca_df.head()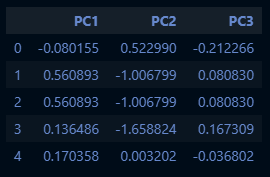

→ 설정한 주성분의 개수로 전체 데이터 분산을 얼만큼 설명 가능한지가 나옴
PC1, PC2, PC3은 base_df의 컬럼이 아님! 주의!!

# 주성분 개수를 판단하기 위한 pca 임의 시행 
pca = PCA(n_components=1)
pca.fit(scale_df)
# 설정한 주성분의 갸수로 전체 데이터 분산을 얼만큼 설명 가능한지 
pca.explained_variance_ratio_.sum()


→ 주성분이 1개인 경우에는 전체 데이터의 분산을 41% 설명할 수 있다는 이야기

  • 주성분 2개로 하면 62%

※주의사항※
주성분의 개수가 5개라고 하면 이 5개가 각각의 컬럼을 의미하는 건 아님!
이거를 하나로 합쳐놓고 성분을 5개를 뺀 것! 컬럼을 가져온 게 아님!! 뭉쳐놓고 차원 축소를 해 놓고 거기서 성분을 5개 뽑은 것!!!

# 초기 k 값 참고를 위한 scree plot 을 그리고, 군집이 나뉘는 시간까지 고려한 k 값 확인 
model = KMeans()

# k 값의 범위를 조정해 줄 수 있습니다. 
visualizer = KElbowVisualizer(model, k=(3,12))

# 데이터 적용 
visualizer.fit(pca_df) 
visualizer.show()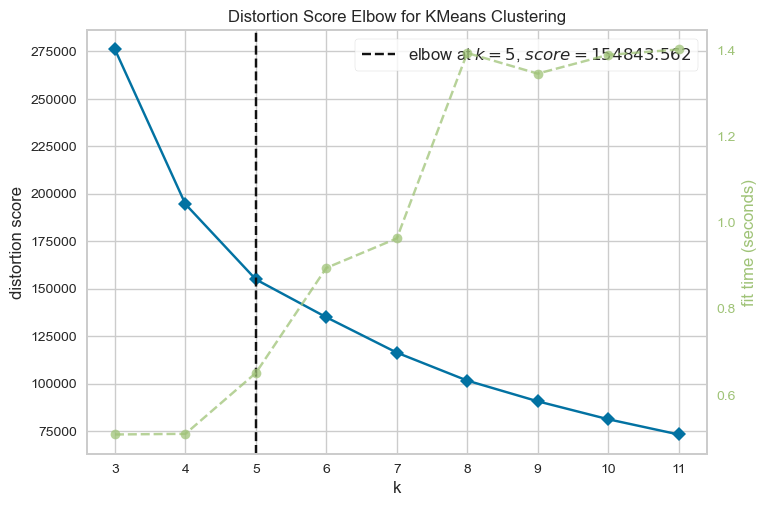   

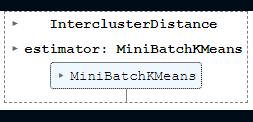
# 초기 k 값 참고를 위한 distance map 시각화
# 그룹의 갯수를 지정해 줄 수 있습니다. 저는 5로 적어두었습니다. 
intercluster_distance(MiniBatchKMeans(5, random_state=42), pca_df)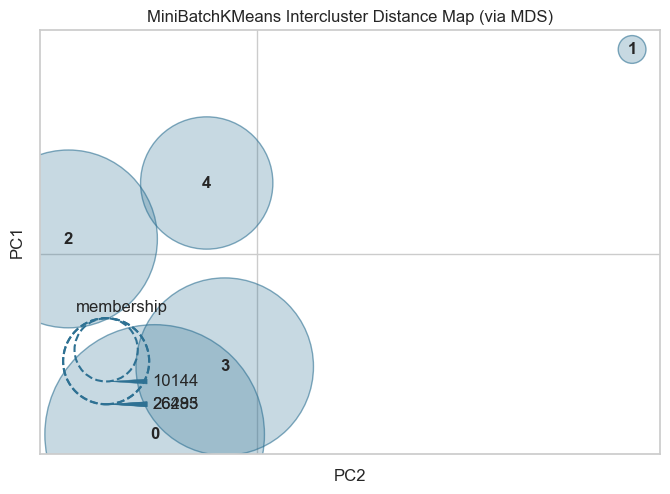


3. 모델 선택 및 학습

#  KMEANS
# 군집개수(n_cluster)는 5,초기 중심 설정방식 랜덤,  
kmeans = KMeans(n_clusters=5, random_state=42,init='random')

# pca df 를 이용한 kmeans 알고리즘 적용
kmeans.fit(pca_df)

# 클러스터 번호 가져오기 
labels = kmeans.labels_

# 클러스터 번호가 할당된 데이터셋 생성
kmeans_df = pd.concat([pca_df, pd.DataFrame({'Cluster':labels})],axis = 1)

# 클러스터 번호가 할당된 데이터셋 생성
kmeans_df.groupby(['Cluster'])['PC1'].count().reset_index()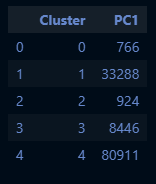

base_df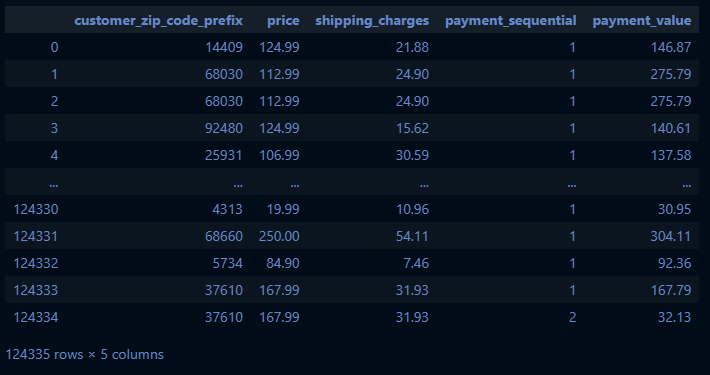

# 3차원으로 시각화 
x =kmeans_df["PC1"]
y =kmeans_df["PC2"]
z =kmeans_df["PC3"]

fig = plt.figure(figsize=(12,10))
ax = plt.subplot(111, projection='3d')
ax.scatter(x, y, z, s=40, c=kmeans_df["Cluster"], marker='o', alpha = 0.5, cmap = 'Spectral')
ax.set_title("The Plot Of The Clusters(3D)")

plt.show()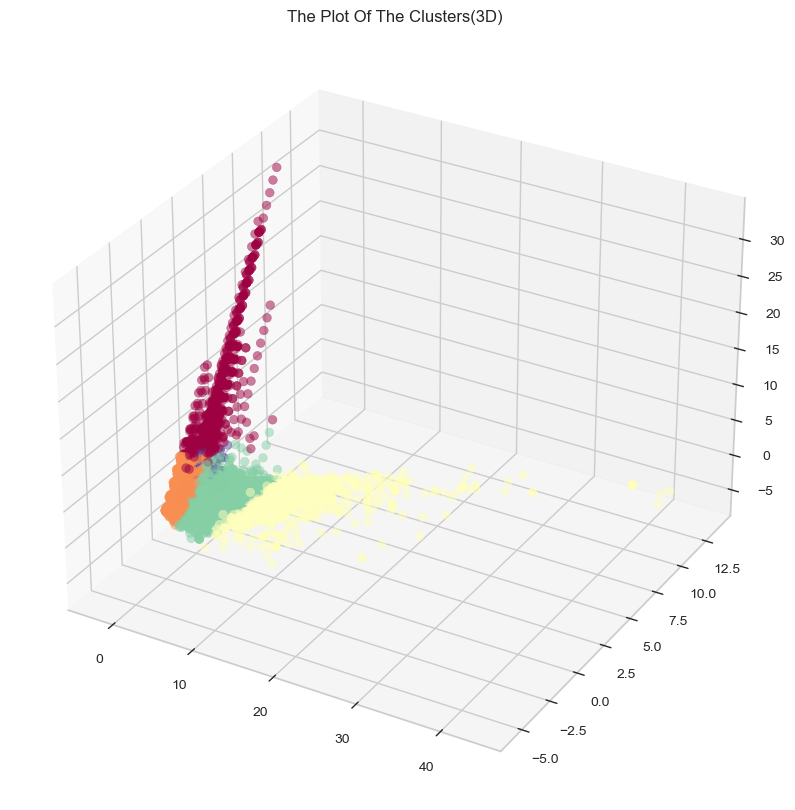

# 2차원으로 시각화

plt.figure(figsize=(8,6))

sns.scatterplot(data = kmeans_df, x = 'PC1', y='PC2', hue='Cluster')
plt.title('The Plot Of The Clusters(2D)')
plt.show()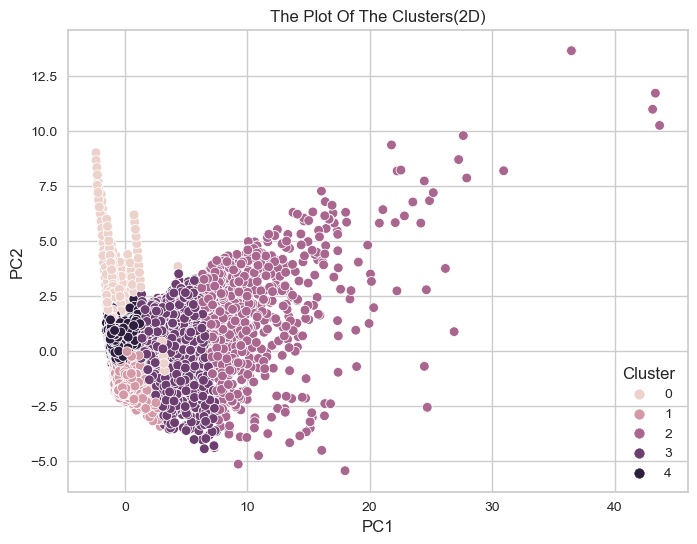

→ 대부분 2차원으로 그려요~
(더 잘 보임)

POINT
고유값은 다 drop
feature는 연속형 범주만 가져오셔야
범주형 쓸 거면 인코딩해야
파생범주 대환영
클러스터링 완료 후 역추적해야 함
(군집별 EDA 진행)
→ 클러스터가 어떤 특성인지는 클러스터 번호를 맨 마지막 컬럼에 붙이고 역추적

profile
Suhyeon Lee
2 B R 0 2 B

0개의 댓글

관련 채용 정보