목표

• 데이터의 통계적 실험 이해
• 대표적인 통계적 실험: A/B 테스트 이론 학습
• 통계적 실험의 유의성(우연인가?): p-value 이해
• 통계적 실험의 검정방식 숙지
• python 코드 작성 및 활용

구분	상세
분석 기법	기초 통계분석
	상관분석
	회귀분석
	분류분석
	군집분석
	RFM 분석
분석 방법론	A/B TEST ← HERE!
통계이론	기초통계이론(평균, 분산, 표준편차) ← DONE
	정규분포와 중심극한정리 ← DONE
	신뢰구간← DONE 유의수준 ← HERE!
	가설 설정 ← HERE!
	통계적 유의성 검정 ← HERE!
	통계적 가설 검정 ← HERE!

데이터 분석가의 통계적 실험

• 실험설계는 특정 가설(의도)을 확인하거나 기각하기 위한 목표를 가지고 있어요!
  • 통계적으로 내가 생각한 것이 의미가 있었는지 알기 위해 통계적 실험 진행
  • 통계적 실험: 내 생각이 통계적으로 유의한지(통계적으로도 괜찮은지) 물어보는 것

분석 기법 선택하기

• 데이터 분석가는 데이터 종류에 따라 알맞은 분석기법을 활용해야 함
  • 1회차에 학습한 데이터 종류 기억하기!
    • 범주형 및 연속형
• 아래 분석기법 선택 그림에서 분홍색 글씨로 표시된 분석기법들을 학습할 예정
  

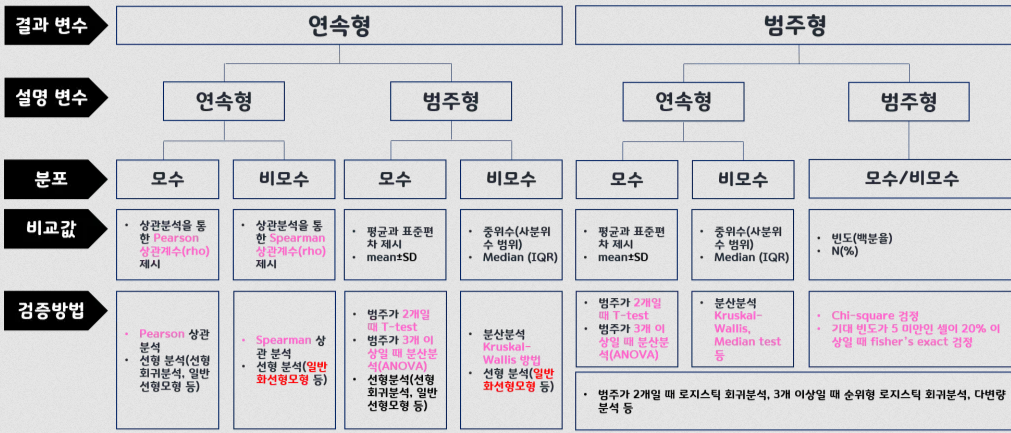
검증 방법

• 피어슨 상관 분석
  • 결과변수
    • 연속형
  • 설명변수
    • 연속형
  • 분포
    • 모수
  • 비교값
    • 피어슨 상관계수(rho)

EDA 하면서 이미 보셨죠?

• 상관관계
  • 연속형-연속형
    (Correlation for continous data)
    • pearson correlation
    • kendall correlation
      *spearman correlation

• 스피어만 상관 분석

  • 결과변수
    • 연속형
  • 설명변수
    • 연속형
  • 분포
    • 비모수
  • 비교값
    • 스피어만 상관계수(rho)

• 선형 분석(일반화선형모형 등)

  • 결과변수
    • 연속형
  • 설명변수
    • 연속형
  • 분포
    • 비모수
  • 비교값
    • 스피어만 상관계수(rho)

• T-test

  • 범주가 2개일 때
  • 결과변수
    • 연속형
  • 설명변수
    • 범주형
  • 분포
    • 모수
  • 비교값
    • 평균, 표준편차 | mean±SD

• ANOVA(분산분석)

  • 범주가 3개 이상일 때
  • 결과변수
    • 연속형
  • 설명변수
    • 범주형
  • 분포
    • 모수
  • 비교값
    • 평균, 표준편차 | mean±SD

• Kruskal-Wallis 방법

  • 결과변수
    • 연속형
  • 설명변수
    • 범주형
  • 분포
    • 비모수
  • 비교값
    • 중위수(사분위수 범위) | Median(IQR)

• 선형분석(일반화선형모형 등)

  • 결과변수
    • 연속형
  • 설명변수
    • 범주형
  • 분포
    • 비모수
  • 비교값
    • 중위수(사분위수 범위) | Median(IQR)

• T-test

  • 범주가 2개일 때
  • 결과변수
    • 범주형
  • 설명변수
    • 연속형
  • 분포
    • 모수
  • 비교값
    • 평균, 표준편차 | mean±SD

• ANOVA(분산분석)

  • 범주가 3개 이상일 때
  • 결과변수
    • 범주형
  • 설명변수
    • 연속형
  • 분포
    • 모수
  • 비교값
    • 평균, 표준편차 | mean±SD

• Kruskal-Wallis 방법

  • 결과변수
    • 범주형
  • 설명변수
    • 연속형
  • 분포
    • 비모수
  • 비교값
    • 중위수(사분위수 범위) | Median(IQR)

• Median test

  • 결과변수
    • 범주형
  • 설명변수
    • 연속형
  • 분포
    • 비모수
  • 비교값
    • 중위수(사분위수 범위) | Median(IQR)

• Chi-square 검정

  • 결과변수
    • 범주형
  • 설명변수
    • 범주형
  • 분포
    • 모수/비모수
  • 비교값
    • 빈도(백분율) | N(%)

이것도 EDA 하면서 나왔어요!

• 상관관계
  • 범주형-범주형(Correlation for categorical data)
    • chi square test
    • Cramer’s V

• fisher's exact 검정
  • 기대 빈도가 5 미만인 셀이 20% 이상일 때
  • 결과변수
    • 범주형
  • 설명변수
    • 범주형
  • 분포
    • 모수/비모수
  • 비교값
    • 빈도(백분율) | N(%)

용어 정리

• 변수: 대상의 속성이나 특성을 측정하여 기록한 것
  • 독립변수
    • 원인이 되는 변수
    • 설명변수라고도 불림
  • 종속변수
    • 결과가 되는 변수
    • 결과변수라고도 불림
    • 독립변수에 따라 그 값이 변할 것이라고 예상하는 변수
• 모수: 모집단을 대표하는 값
• 모수통계
  • 모집단이 정규분포를 따른다는 가정 하에 사용
  • 데이터 분석가는 주로 모수통계를 진행
  • 평균, 분산 등의 값을 알고 있다는 가정 하에 진행하는 통계분석
• 비모수통계
  • 모집단이 정규분포가 아닐 때 사용
    • 모집단이 정규분포가 아님
      == 표본의 크기가 충분히 크지 않음
      → 소규모 실험에 해당
  • 또는 평균, 분산 등의 값을 가정하지 않고 진행하는 통계분석

A/B 테스트에 필요한 3가지 통계적 지식

• A/B 테스트: 방법론 중 하나임

1. 가설설정
2. 통계적 의미 해석(P-value)
3. 가설검정(T검정, 카이제곱검정)

상황에 알맞은 분석 설계 및 진행

👨 사업: 안녕하세요~! 이번 제품의 가격이 지난번 가격보다 수익성이 좋을까요?
→ 굉장히 불친절한 질문(기준도 없고 기간도 없음)
→ A부터 B까지의 데이터와 C부터 D까지의 데이터를 비교해 주시고 환불 건은 제외해 주시고… 🡆 디테일하게 가이드가 와야 함!
👩 분석: select 가격 from 매출테이블… 네네 살펴보고 말씀드릴게요.
→ 데이터를 추출할 때 필요한 기준들이 필요: 보통 다시 물어봐야 함

• 데이터분석가는 현업에서 다른 팀의 요청을 받거나, 혹은 프로젝트를 진행하며 능동적으로 분석을 설계
  1. 데이터의 유형과 분포를 먼저 살피기
  2. 여러 통계적 실험 중에서 어떤 실험을 진행할 것인지 결정

통계적 실험

• 정의
  • 어떤 목적을 가지고 관찰을 통해 결과(측정값) 얻어내는 것
• 목적
  • 통계적 추론을 통해 보다 진실에 가까운 값을 도출
    • 예시
      : 모든 까마귀는 검정색이다.(가설) → (관찰) → 모든 까마귀가 검정색이 아닐 수도 있지만 전세계에 있는 까마귀를 모두 확인하는 것은 불가능하다. → 통계적 추론 실시 → 진실에 가까운 값 도출
      🡆 연역법처럼 보이지만 "확률성"을 내포하므로 귀납법의 다른 형식이라고 함
  • "제한된 환경에서의 관찰을 통해 확보된 사실을 바탕으로 제한된 결론을 내리고, 확률적 판단으로 제한된 결론을 내려 진실에 가까운 값 도출"
• 프로세스
  • 가설 수립 → 실험 설계 → 데이터 수집 → 추론 및 결론 도출

A/B TEST

비즈니스 마케팅 시 필수

개념 이해

• A/B 테스트

  • 마케팅 고객 데이터 분석 중 가장 널리 사용되는 방법
  • 오래전부터 과학에서 쓰여왔던 대조실험(가설을 입증하기 위해 대조군, 실험군을 설정하고 검증)과 동일
    • 테스트 과정에서 다양한 통계적 개념을 바탕으로 실험 진행

• A/B 테스트의 목적

  1. 고객의 니즈 파악
  2. 최소 투자로 최대 이익 창출(ROI 상승)

• 기업에서는 고객에게 최고의 서비스 경험을 제공하기 위해 자체적으로 A/B테스트 툴을 만들기도 함

→ A/B 테스트는 이렇게 TEST 그룹과 CONTROL 그룹으로 나뉘어 진행되나 꼭 2개의 그룹으로 나눌 필요는 없음

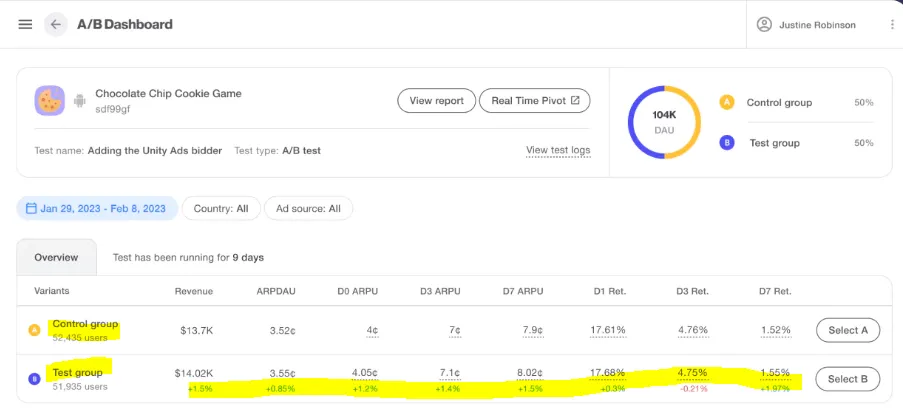
핵심 개념 정리

• 정의

  • 두 가지 처리 방법 중 어떠한 쪽이 더 좋다라는 것을 입증하기 위해 실험군을 두 그룹으로 나누어 진행하는 실험
  • 버킷테스트 또는 분할 테스트라고 불림
  • 종종 두 가지 처리 방법 중 하나는 기준이 되는 기존 방법이거나 아예 아무러 처리도 적용하지 않는 방법이 됨

• 목적

  • UI/UX 개선
    • 서비스에 진입한 방문자의 니즈에 알맞게 UI,UX 가 친절하지 않은 경우 이탈할 가능성이 있음
    • 고객이 될 수 있었던 방문자를 놓치지 않으려면 A/B TEST를 통해 이를 개선하는 작업이 중요
      "이 페이지에서는 구매버튼을 찾기 어렵구나!"
  • 전환율 증가
    • A/B TEST를 통해 무엇이 효과가 있는지(또는 없는지) 파악하면 전환율 상승에 도움
      "c배너보다 d 배너의 전환이 더 좋구나!"
      → 광고 구좌(광고의 자리)도 영향을 줌
      구좌는 Inventory라고도 하며, 1개의 광고 영역에 롤링되어 노출되는 광고 개수를 말함
  • 매출 증가
    • A/B TEST 를 통해 UX가 개선되면 전환율이 상승할 뿐만 아니라, 브랜드에 대한 고객 충성도도 높아짐
    • 이는 곧 반복 구매로 이어져 매출 증가에 영향을 미치게 됨

• 주요 지표

  • 서비스 가입률
  • 재방문율
  • CTR(Click Through Ratio; 노출 대비 클릭률), CVR(ConVersion Rate; 클릭 대비 전환율, 구매전환율)
  • ROAS(캠페인 비용 대비 캠페인 수익)
  • eCPM(1,000회 광고 노출당 얻은 수익)

프로세스

• A/B 테스트는 크게 다섯가지 단계로 진행
  • 모든 단계에서 통계적 개념을 필요로 함

1. 현행 데이터 탐색
   • 앞서 살펴본 주요 지표를 기준으로 현재 데이터 탐색
2. 가설 설정
   • 비즈니스 목표를 달성하는 데 필요한 KPI 정의
     • KPI: Key Performance Indicator; 핵심 성과 지표
   • KPI 전환율을 증가를 위한 귀무가설, 대립가설을 설정
   • 귀무 가설
     • 통계학에서 처음부터 버릴 것을 예상하는 가설
     • 차이가 없거나 의미 있는 차이가 없는 경우의 가설
       "새로운 광고배너를 게재해도 기존과 차이가 없을 것이다"
   • 대립 가설
     • 귀무가설에 대립하는 명제
       "새로운 광고배너를 게재하면 기존과 차이가 있을 것이다(다를 것이다)"
3. 유의수준 설정
   • 귀무가설이 맞을 때 오류를 얼마나 허용할 것인지 기준을 정하는 단계
4. 테스트 설계 및 진행
   • 사용자를 대조군과 실험군의 두 그룹으로 분리
   • 대조군 그룹에게는 제품이나 서비스의 현재 버전을 보여주고, 실험군 그룹에게는 새 버전을 노출 처리
5. 테스트 결과 분석
   • 측정 항목(가설)에 대해 두 그룹의 결과를 분석(검정통계량 분석)
   • 통계적 방법으로 결과를 분석하여 대조군과 실험군 사이의 통계적으로 유의미한 차이가 있는지 확인

주의사항

• 적절한 표본 크기
  • 표본의 크기가 충분하지 않으면 유의미한 결과를 얻을 수 없음
  • 적절한 표본 크기를 결정하고, 그에 맞는 시간과 자원을 투자해야 함
• 하나의 변수만 변경
  • A/B 테스트에서는 하나의 변수만을 변경해야 함
  • 두 가지 이상의 변수를 동시에 변경하면 어떤 변수가 영향을 미쳤는지 파악할 수 없음
• 무작위성
  • A/B 테스트는 무작위로 선택된 사용자들에게 각각 다른 변수를 적용해야 함
• 적절한 분석 방법
  • A/B 테스트 결과를 해석할 때는 가설 검증을 위한 통계적 분석 방법을 선택하고, 유의수준을 설정해야 함
• 테스트 결과의 의미
  • A/B 테스트 결과가 통계적으로 유의미하더라도 항상 실제로 의미 있는 결과인지 한번 더 생각해보아야 함
• 정해진 기간 동안 진행
  • A/B 테스트는 동일한 기간 동안 진행되어야 함
    • 그 기간 동안에만 결과를 수집하고, 분석
  • 너무 짧은 기간 동안에는 결과를 수집하기 어렵고, 너무 긴 기간 동안에는 사용자들의 행동이 변할 가능성이 있음

유의수준 설정하기

신뢰수준의 반대 개념

중심극한정리 복습

• 갈턴 보드
  
  • 확률 분야에서 가장 두드러지는 분포인 정규분포(= 종 모양 곡선, 가우스 분포)를 보여줌
    • 비슷한 인구 통계에 속하는 많은 사람들을 대상으로 키를 조사하면 정규분포를 따름
    • 길이가 정말 긴 자연수들을 대상으로 각 숫자가 가진 소인수의 개수를 새면 그 개수의 모음 역시 어떤 정규분포에 가까워짐: Erdős–Kac theorem

• 중심극한정리
  • 정규분포를 흔하게 볼 수 있는 이유를 설명하는 핵심적인 사실
  • 표본수집을 기반으로 한 추리통계에서 모집단의 분포가 어떤 모양이더라도 모집단의 크기가 충분히 크다면 표본평균의 분포가 정규분포를 이룬다는 이론
    • 이를 통해, 모집단의 모수를 추정할 수 있음

유의수준

• 표본을 추출하는 순간 모집단과 100% 일치할 수 없기 때문에, 오류의 가능성이 존재
• 가설 검정에서 결론을 해석하기 위해서는 기준을 세우고, 그 기준을 만족하는지 확인해야 함
  • 여기서 기준이 되는 것이 유의수준

구분	상세
정의	귀무가설(차이가 없을 것이라고 생각하는 가설)이 맞을 때 기각할 확률
표기	α
범용적 기준	• 0.05(5%) • 0.01(1%) • 0.10(10%)
신뢰도와의 관계	95%의 신뢰도를 기준으로 한다면 (1−0.95)인 0.05 값이 유의수준 → 즉 반대의 개념

• 유의수준에 대한 내용을 이해하기 위해, 정규분포 그래프를 살펴보기
  
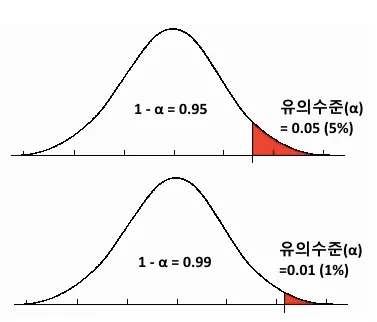
  • 그래프 면적은 확률을 의미하므로, 0부터 1 사이의 값을 가짐
  • 유의수준을 0.05로 설정 → 즉 95% 신뢰도로 기준을 정한 것

검정통계량과 p-value

유의수준을 정하고 실험을 진행했어요.
결과를 해석하고 싶어요!

검정 방식 정하기 & 검정통계량 계산하기

• 지금까지 가설을 설정하고 유의수준을 정했으니 실험을 완료한 뒤, 실험 전과 후를 비교하면서 유의미했는지 살펴보기

  • 결론적으로 귀무가설을 채택할지, 기각할지 결정할 수 있어야 함

• 검정통계량

  • 귀무가설을 채택 또는 기각하기 위해 사용하는 확률변수
    • 확률변수: 특정 확률로 발생하는 각각의 결과를 수치값으로 표현하는 변수
    • 즉 확률에 대한 수치 → 0과 1 사이의 값

[예제]
주사위를 던졌을 때 나오는 숫자를 확률변수 X 라고 가정했을 때, 각 X 에 대한 확률 P(X) 를 구하시오.
→ 확률변수 X는 1,2,3,4,5,6 입니다.
→ 주사위 값이 1~6 중 어떤 수가 나올지 모르기 때문에 우리는 이를 확률변수라고 합니다.
→ 각 X 에 대한 확률은 1/6 입니다.

• 검정통계량은 표본 평균, 비율, 상관 계수 간의 차이 등 다양한 형태를 취할 수 있음
• 검정 방식의 선택은 가설과 데이터 종류에 따라 달라짐

활용 대상 ★★★

• Z 검정
  • 표본의 평균 비교
  • 모집단의 표본을 알 수 있는 경우
  • 집단 개수: 주로 2개
• T 검정
  • 표본의 평균 비교
  • 모집단의 표본을 알 수 없는 경우
  • 집단 개수: 주로 2개
• 카이제곱 검정
  • 표본의 비율이나 빈도 비교
  • 집단 개수: 주로 2개 이상
• F 검정
  • 두 개 이상 그룹의 분산 비교
  • 세 개 이상의 집단 간 평균의 차이 비교
  • 회귀식 검정
  • 집단 개수: 주로 3개 이상

검정 방식	검정통계량	범위	대상
Z검정	Z-value	-∞ ~ ＋∞	연속형 자료
T검정	t-value	-∞ ~ ＋∞	연속형 자료
카이제곱검정	$x^2$-value	0 ~ ＋∞	범주형 자료
F검정	F-value	0 ~ ＋∞	범주형 자료

p-value ★★★

• 어떤 사건이 우연히 발생할 확률
• Probability-value 의 줄임말로 ‘확률’을 뜻함
  • 확률이므로, p-value 는 0 이상이고 1 이하의 값을 가짐
• 우리의 목표는 대립가설 채택이므로, 우연히 일어날 확률이 작으면 좋음
  • 즉 유의수준보다 p-value 가 작은 경우에 우연히 일어날 가능성이 거의 없어 대립가설을 채택
    • p-value가 0.05 보다 작다
      = 우연히 일어났을 가능성이 거의 없다
      = 인과관계가 있다고 추정
      = 대립가설 채택
    • p-value가 0.05 보다 크다
      = 우연히 일어났을 가능성이 높다
      = 인과관계가 없다고 추정
      = 대립가설 기각

정규분포 그래프에서 p-value 확인

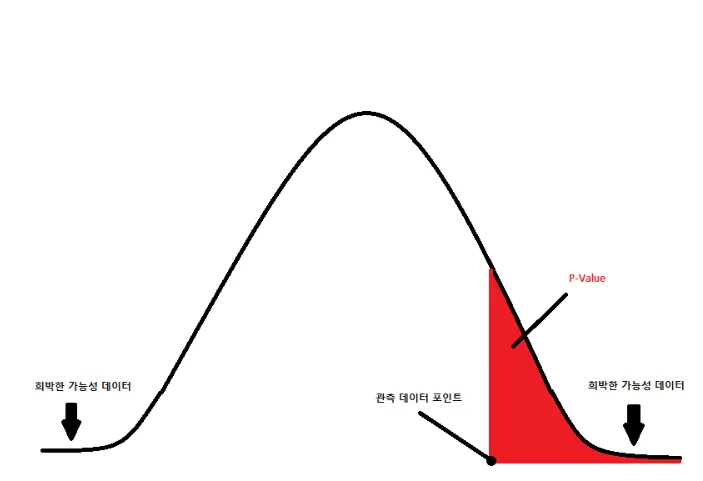
• 중심극한정리를 통해, 모집단이 큰 경우 표본평균이 정규분포를 따르게 된다고 가정
  • 정규분포의 그래프 아래쪽이 확률값이라는 사실을 기억
  • 유의 수준을 설정하고, p-value 를 도출해서 의미를 해석한다는 점 역시 잊으면 안 됨

더 알아보기

검정 방식과 검정 통계량을 설정했는데, 모두 계산해야 할까?

• python library 를 통해서 계산!

🧑(데이터분석가) : scipy library 불러와서 t-value 계산해줘
📒(라이브러리): 두두둥 여기 있습니다.

요약

• 데이터분석가는 데이터 종류에 따라 알맞은 분석기법을 활용해야 함
• A/B 테스트라는 방법론을 통해 해당 과정에서 사용되는 통계개념 학습
  • 가설설정, 통계적 의미 해석, 가설검정
• A/B 테스트는 5가지 단계로 진행
  • 현행 데이터 탐색 → 가설설정 → 유의수준설정 → 실험 → 해석
• 귀무가설과 대립가설의 의미
  • 귀무가설은 차이가 없거나 의미 있는 차이가 없는 경우의 가설
  • 대립가설은 차이가 있는 경우의 가설
• 유의수준은 신뢰도의 반대 개념
  • 오류의 허용 범위
    - 일반적으로 0.05를 사용
    - 이는 곧 신뢰도 95% 를 의미
    -p-value는 어떠한 사건이 우연하게 발생할 확률
  • p-value가 0.05 보다 작다
    = 우연히 일어났을 가능성이 거의 없다
    = 인과관계가 있다고 추정
    = 대립가설 채택
• python library를 통해서 가설검정을 진행