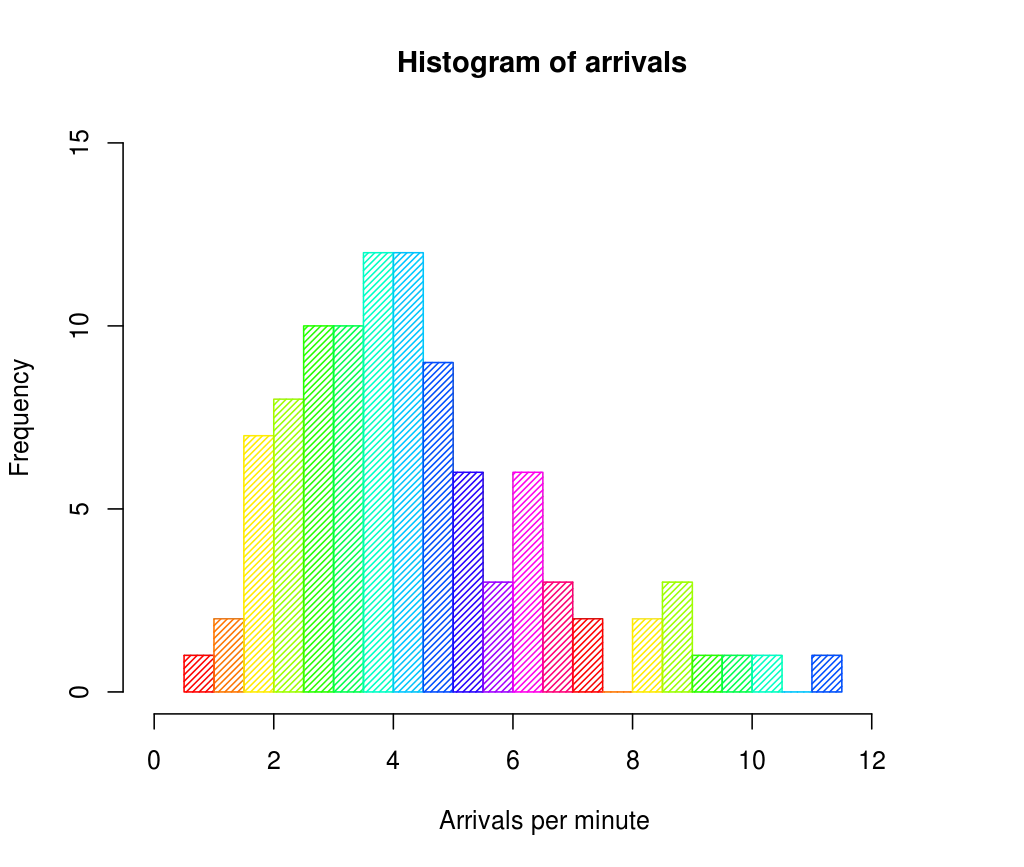목표

• 함수에 대해 이해하고 어떤 코드든 함수 형태로 만들 수 있다.

파이썬의 몸통 : 함수

• 파이썬을 보다 편리하게 사용할 수 있게 해주는 함수
• 일반적으로 파이썬 코드를 작성할 때 긴 길이의 코드를 작성하는 경우가 많고 같은 코드를 동일하게 다양한 상황에서 사용해야 하는 상황들이 많음
• 이럴 때 함수 형태로 한번 만들어 두면 그 다음부터 언제든 함수 이름만 호출하면 편하게 그 안에 있는 코드들을 실행할 수 있음

결과물 미리보기

• 함수를 활용하여 긴 길이의 코드를 하나로 묶어 효과적으로 활용 가능
• 설명
  • 머신러닝과 딥러닝: 하나의 거대한 함수
  • 데이터 처리하는 하나의 흐름(과정)을 함수로 제작 가능
• 목적
  • 파이썬 코드를 하나의 함수로 묶어놓아 보다 효율적으로 사용 가능
• 기대효과
  1. 훨씬 더 길고 복잡한 코드들을 함수로 만들 수 있다.
  2. 간결하게 다양한 작업들을 수행할 수 있다.

함수 기본 배우기

1) 함수란?

개념

• 입력을 받아 원하는 처리를 한 후 출력을 내보내는 일련의 작업을 수행하는 코드 블록
  • 입력이 없거나 출력이 없는 함수도 종종 있지만 기본적으로는 입력값, 출력값 항상 생각해 줘야 함
• 프로그램 내에서 특정한 기능을 수행하기 위해 코드를 논리적으로 그룹화하여 재사용 가능한 형태로 정의

필요성

• 코드 재사용
  • 반복되는 코드를 함수로 정의하여 여러 곳에서 재사용
• 모듈화
  • 프로그램을 여러 개의 작은 모듈로 나누어 개발 및 관리
• 유지 보수 용이성
  • 함수는 각각의 기능을 독립적으로 정의하므로, 수정이나 확장이 필요할 때 해당 함수만 수정
• 가독성 향상
  • 함수는 코드의 의도를 명확하게 표현할 수 있으며, 복잡한 작업을 함수로 분해하여 이해하기 쉽게 만듦

함수 정의와 호출 방법

• 함수 정의
  • def 키워드를 사용하여 함수를 정의
  • 함수 이름 뒤에 소괄호 안에 매개변수(입력 값)를 정의
    • 매개변수: 함수 내에서 사용되어지는 변수
  • 함수 내부에서 필요한 작업을 수행한 후, return을 사용하여 결과값을 반환

def 함수이름(매개변수1, 매개변수2, ...):
    # 함수 내부에서 수행할 작업
    return 결과값  # (선택적) 함수의 결과를 반환

• 함수 호출
  • 함수를 호출할 때는 함수 이름을 적고, 소괄호 안에 인수(함수에 전달할 값)를 넣어 호출
    • 인수: 함수에 입력값으로 들어가는 변수
  • 필요에 따라 결과를 변수에 저장

결과 = 함수이름(인수1, 인수2, ...)

예시

• 이름을 전달하면 해당 이름과 함께 인사말을 반환하는 간단한 함수 정의
  • greet라는 함수를 정의하여 함수를 호출하면 반환된 인사말을 출력
  • 함수를 사용하면 코드를 구조화하고 재사용 가능한 모듈로 만들 수 있음

# 함수 정의
def greet(name): # name: 매개변수
    message = "Hello, " + name + "!"
    return message

# 함수 호출
greeting = greet("Alice") # "Alice": 인수
print(greeting)  # 출력: Hello, Alice!

2) 간단한 계산의 함수 만들기

평균 계산 함수

def calculate_mean(numbers):
    """
    주어진 숫자 리스트의 평균을 계산하는 함수

    Parameters:
    numbers (list of int or float): 평균을 계산할 숫자들의 리스트

    Returns:
    float: 주어진 숫자 리스트의 평균값
    """
    total = sum(numbers)
    mean = total / len(numbers)
    return mean

# 함수 호출 및 예시
data = [10, 20, 30, 40, 50]
average = calculate_mean(data)
print("평균:", average)

• 주어진 숫자 리스트의 평균을 계산하는 간단한 데이터 분석 계산을 수행
  • calculate_mean이라는 함수를 정의하여 주어진 숫자 리스트의 평균을 계산
  • 숫자 리스트를 받아서 sum() 함수를 이용해 총합을 구하고, 리스트의 길이로 나누어 평균을 계산합니다. 그리고 그 값을 반환
  • 이 함수를 호출할 때는 숫자 리스트를 인수로 전달하면 됨
• 위의 코드에서는 [10, 20, 30, 40, 50]라는 리스트를 전달하여 평균을 계산하고 출력함
• 이러한 함수는 데이터 분석에서 계산을 수행할 때 유용하게 사용될 수 있음

3) 다양한 함수 예시

• 조건문, 반복문, 리스트, 튜플, 딕셔너리 등을 활용한 다양한 함수

숫자 리스트에서 최대값을 찾는 함수

def find_max(numbers):
    max_num = numbers[0]
    for num in numbers:
        if num > max_num:
            max_num = num
    return max_num

# 함수 호출
print(find_max([3, 7, 2, 9, 5]))  # 출력: 9

튜플의 모든 요소를 곱하는 함수

def multiply_tuple(tup):
    result = 1
    for num in tup:
        result *= num
    return result

# 함수 호출
print(multiply_tuple((2, 3, 4)))  # 출력: 24

주어진 문자열에서 각 문자의 출현 빈도를 딕셔너리로 반환하는 함수

def char_frequency(string):
    freq_dict = {}
    for char in string:
        if char in freq_dict:
            freq_dict[char] += 1
        else:
            freq_dict[char] = 1
    return freq_dict

# 함수 호출
print(char_frequency("hello"))  # 출력: {'h': 1, 'e': 1, 'l': 2, 'o': 1}

함수 심화 배우기

1) 전역변수와 지역변수의 차이

전역변수 (Global Variables)

• 프로그램 전체에서 접근 가능한 변수
• 어디서든지 사용할 수 있음
• 프로그램이 시작될 때 생성되고, 프로그램이 종료될 때까지 메모리에 유지됨
• 프로그램의 어디서든지 접근할 수 있으므로, 여러 함수에서 공통적으로 사용되는 값을 저장할 때 유용
• 너무 많은 전역변수를 사용하면 코드의 가독성이 떨어지고 디버깅이 어려워질 수 있음

지역변수 (Local Variables)

• 특정한 범위(예: 함수 내부)에서만 접근 가능한 변수
• 해당 범위를 벗어나면 사용할 수 없음
• 지역변수는 해당 범위에서 생성되고, 범위를 벗어나면 메모리에서 사라짐
  • 함수 내에서 정의된 변수는 해당 함수 내에서만 사용 가능한 지역변수임
• 지역변수는 함수 내에서만 사용되므로, 해당 함수에서만 유효하고 다른 함수나 코드 블록에서는 사용할 수 없음
• 함수가 실행될 때 생성되고, 함수가 종료되면 메모리에서 제거되므로 메모리 관리에 효율적

예시

# 전역변수 예시
global_var = 10

def global_example():
    print("전역변수 접근:", global_var)

global_example()  # 출력: 전역변수 접근: 10

# 지역변수 예시
def local_example():
    local_var = 20
    print("지역변수 접근:", local_var)

local_example()  # 출력: 지역변수 접근: 20

# 함수 내에서 전역변수를 수정하는 예시 ★
def modify_global():
    global global_var
    global_var = 30
    print("함수 내에서 수정된 전역변수:", global_var)

modify_global()  # 출력: 함수 내에서 수정된 전역변수: 30
print("수정된 전역변수 확인:", global_var)  # 출력: 수정된 전역변수 확인: 30

• 위의 코드에서 global_var는 전역변수
  • 프로그램 어디서든지 접근 가능
• local_var는 함수 local_example() 내에서만 접근 가능한 지역변수
• 함수 내에서는 global 키워드를 사용하여 전역변수를 수정할 수 있음
  • 함수 내에서 전역변수를 수정하더라도, 해당 변수는 전역적으로 수정됨

global 키워드를 안 쓰면 어떻게 될까?

global_var = 10
def modify_global():
    global_var = 30
    print("함수 내에서 수정된 전역변수:", global_var)
modify_global()  # 출력: 함수 내에서 수정된 전역변수: 30
print("수정된 전역변수 확인:", global_var)  # 출력: 수정된 전역변수 확인: 10

global 키워드 문법 사용하지 않으면 전역변수 수정 안 됨
함수 내부적으로 30을 출력했을 뿐
함수 내부에 있는 global_var는 진짜 전역변수가 아니라 이름만 같은 지역변수임 → 값 변화시켜도 전역변수에 영향 없음

2) 인수(argument)와 매개변수(parameter)의 차이

• 매개변수(parameter)와 함수를 호출할 때 전달되는 값(argument; 인수 혹은 전달인자라고 표현하기도 해요)은 혼동하기 쉬운 개념

매개변수(Parameter)

• 함수를 정의할 때 함수가 받아들이는 값을 지정하는 변수
• 함수의 헤더 부분에서 매개변수가 정의되며, 함수 내부에서 사용됨
• 함수를 정의할 때 매개변수를 정의하고, 함수가 호출될 때 매개변수에 해당하는 값을 전달받음

인수(Argument)

• 함수를 호출할 때 함수에 전달되는 값
• 함수를 호출할 때 전달되는 실제 값
  • 함수를 호출할 때마다 다를 수 있음
• 함수 호출 시 매개변수에 전달되는 값으로, 해당 값은 함수 내부에서 매개변수로 사용
• 전달인자라는 표현으로도 사용

예시

# 매개변수(parameter) 예시
def greet(name):  # 여기서 'name'은 매개변수입니다.
    print("Hello, " + name + "!")
    
# 함수 호출할 때 전달되는 값이 인수(argument)입니다.
greet("Alice")  # 함수 호출 시 "Alice"는 greet 함수의 매개변수 'name'에 전달됩니다.

• 위 코드에서 greet 함수의 매개변수는 name
• 이 함수를 호출할 때 "Alice"라는 값이 name 매개변수로 전달되는데, 여기서 "Alice"가 인수에 해당

더 복잡한 예시

def add_numbers(x, y):  # 'x'와 'y'는 매개변수입니다.
    result = x + y
    return result

# 함수 호출 시 10과 20이 각각 'x'와 'y' 매개변수에 전달됩니다.
sum_result = add_numbers(10, 20)  # 10과 20이 전달인자(Argument; 인수)입니다.
print("Sum:", sum_result)  # 출력: Sum: 30

• add_numbers 함수의 매개변수는 x와 y
• 이 함수를 호출할 때 10과 20이 각각 x와 y 매개변수로 전달되는데, 이 10과 20이 각각 인수에 해당
• 함수 내부에서는 이 인수들을 이용하여 연산 수행

3) 위치 인수 (Positional Arguments)란?

• 함수 호출 시 전달되는 인자(argument)의 두 가지 유형 중 하나
  • 나머지 하나는 키워드 인수(keyword argument)
• 함수 정의에서 매개변수(parameter)의 위치에 따라 전달되는 인수
• 인자의 값이 함수의 매개변수에 순서대로 매핑됨

def greet(name, age):
    print("안녕하세요", name, "님! 나이는 ", age, "세입니다.")

# 위치 전달인자 사용
greet("철수", 30)  # 출력: 안녕하세요, 철수님! 나이는 30세입니다.

• 함수 호출 시 위치 전달인수는 매개변수의 위치에 따라 전달됨
  • 위 예시에서는 "철수"가 name 매개변수에, 30이 age 매개변수에 순서대로 전달
    (인수로 넣는 순서에 따라서 매개변수의 값이 순서대로 들어감)

4) 키워드 인수 (Keyword Arguments) 설정

• 함수를 호출할 때, 인수를 순서대로 전달하는 대신에 특정 매개변수에 값을 할당하여 전달

def greet(name, age):
    print("이름:", name)
    print("나이:", age)

# 키워드 인수를 사용하여 함수 호출
greet(name="Alice", age=30)

• 위의 코드에서 greet 함수는 name과 age 두 개의 매개변수를 가짐
• 함수를 호출할 때, 각 매개변수에 직접 값을 할당하여 전달하고 있음

5) 기본값 (Default Values) 설정

• 함수의 매개변수에 기본값을 설정할 수 있음
  • 해당 매개변수에 인수가 전달되지 않았을 때 기본값으로 사용

def greet(name="Guest", age=25):
    print("이름:", name)
    print("나이:", age)

# 기본값이 설정된 함수 호출
greet()

• 위의 코드에서 greet 함수의 매개변수인 name과 age는 각각 "Guest"와 25의 기본값을 가집니다.
  • 함수를 호출할 때 인수를 전달하지 않으면 기본값 사용

6) 키워드 인수와 기본값을 함께 사용

• 키워드 인수와 기본값을 함께 사용하여 함수를 호출

def greet(name="Guest", age=25):
    print("이름:", name)
    print("나이:", age)

# 키워드 인수를 사용하여 함수 호출
greet(name="Alice", age=30)

# 일부 매개변수에만 키워드 인수 사용하여 호출
greet(name="Bob")

• 위의 코드에서는 greet 함수를 호출할 때 키워드 인수를 사용하여 name과 age에 값을 전달
• 또한 일부 매개변수에만 키워드 인수를 사용하여 값을 전달할 수 있음
• 함수의 매개변수에 기본값이 설정되어 있으면 해당 매개변수에 값을 전달하지 않아도 기본값이 사용됨

7) 가변 인수 (Variable-length Arguments) 활용

• 여러 개의 인수들을 받을 수 있는 함수를 만들기 위해 활용
  • 인수가 몇 개 들어갈지 모르는 상황에서 사용
• 파이썬에서는 *args와 **kwargs를 사용
  • *args(arguments): 함수를 호출할 때 임의의 개수의 위치 인수를 전달할 수 있도록 함
    • asterisk가 핵심임(여러 개의 인수를 받는다는 표시)
    • c언어 포인터(주소값 저장)와 헷갈리지 말기 → 난 c언어 모르니까 헷갈릴 일이 없겠군...
    • 꼭 args라고 쓸 필요 없음(*a도 되고 *myname도 되고 원하는 단어 다 됨)
    • 일반 변수보다는 뒤에 위치해 있어야 함!(파이썬은 어디서부터 어디까지를 *변수에 담을지 알 수 없기 때문)
  • **kwargs(keyword argument): 함수를 호출할 때 임의의 개수의 키워드 인수를 전달할 수 있도록 함

*args 예시 ★

def sum_values(*args):
    total = 0
    for num in args:
        total += num
    return total

result = sum_values(1, 2, 3, 4, 5)
print("합계:", result)  # 출력: 합계: 15

• 함수 sum_values는 임의의 개수의 위치 인수를 받아서 그 합계를 계산
• 함수 내에서는 args라는 튜플로 위치 인수들을 받아 처리

**kwargs 예시: 키워드 인수 받기

def print_info(**kwargs):
    for key, value in kwargs.items():
        print(f"{key}: {value}")

print_info(name="Alice", age=30, country="USA")

• print_info 함수는 임의의 개수의 키워드 인수를 받아서 그 정보를 출력

• 함수 내에서는 kwargs라는 딕셔너리로 키워드 인수들을 받아 처리

• 우리가 사용하는 함수 중에서도 kwargs가 있음

  • 사용자가 원하는 방식대로 동작하게 하는 함수
    • keyword argument와 기본값이 사용된 예시

# 1번
print("안녕하세요, 파이썬 재미있나요?")
print("네, 정말 재미있습니다.")

# 2번
print("안녕하세요, 파이썬 재미있나요?", end="(사실 재미없어요...)")
print("네, 정말 재미있습니다.")

'''
1번 출력:
안녕하세요, 파이썬 재미있나요?
네, 정말 재미있습니다.

→ 파라미터에 기본값이 \n(개행문자)로 되어있음 

2번 출력:
안녕하세요, 파이썬 재미있나요?(사실 재미없어요...)네, 정말 재미있습니다.
'''

요약:

• *변수: 여러 개가 argument로 들어올 때 함수 내부에서 해당 변수를 튜플로 처리
• **변수: keyword=''로 입력할 경우 그걸 각각 key와 value로 가져오는 딕셔너리로 처리
• 함수의 파라미터 순서
  • 일반변수 → *변수 → **변수

8) 함수가 데이터 분석에서 사용되는 예시

데이터 전처리 함수

• 데이터 분석을 진행할 때 데이터 전처리는 매우 중요 → 이를 위해 다양한 전처리 함수를 사용
• 데이터 정규화, 결측치 처리, 특성 스케일링 등의 함수를 사용하여 데이터를 전처리할 수 있음

def stadardization(data):
    # 데이터 표준화 함수
    scaled_data = (data - data.mean()) / data.std()
    return scaled_data

def impute_missing_values(data):
    # 결측치 처리 함수
    filled_data = data.fillna(data.mean())
    return filled_data

def nomalization(data):
    # 데이터 정규화 함수
    scaled_data = (data - data.min()) / (data.max() - data.min())
    return scaled_data

정규화(Normalzation), 표준화(Standardization), 결측값(Missing Values)에 대한 부가 설명

• 정규화(Normalization)
  • 데이터를 일정한 범위로 변환하여 비교나 분석을 용이하게 하는 과정
  • 주로 0과 1 사이의 값으로 변환하거나 -1과 1 사이의 값으로 변환하는 등의 방법 사용
• 표준화(Standardization)
  • 데이터의 평균을 0으로, 표준편차를 1로 만들어주는 데이터 전처리 과정
  • 주로 데이터의 분포를 정규분포로 만들거나, 특성 간의 스케일을 일치시키기 위해 사용
  • 일부 머신러닝 알고리즘에서 가정하는 가우시안 분포를 만족시키는 데 도움이 됨
• 결측값(Missing Values)
  • 데이터에서 측정되지 않거나 없는 값을 의미
  • 데이터 수집 과정에서 발생할 수 있거나, 처리 과정에서 발생할 수 있음
  • 분석이나 모델링 과정에서 문제를 일으킬 수 있으며, 이를 처리하는 방법이 중요
  • 데이터 전처리 과정에서 결측값을 채우거나, 해당 행이나 열을 삭제하여 처리하거나, 평균이나 중앙값으로 결측값을 대체하는 등의 방법을 사용

데이터 시각화 함수

• 데이터를 시각화하여 탐색적 데이터 분석을 수행할 때 다양한 시각화 함수를 사용할 수 있음
• 데이터의 분포, 상관 관계, 이상치 등을 확인

import matplotlib.pyplot as plt

def plot_histogram(data):
    # 히스토그램을 그리는 함수
    plt.hist(data, bins=20)
    plt.xlabel('Value')
    plt.ylabel('Frequency')
    plt.title('Histogram of Data')
    plt.show()

def plot_scatter(x, y):
    # 산점도를 그리는 함수
    plt.scatter(x, y)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.title('Scatter Plot')
    plt.show()

히스토그램과 산점도

• 히스토그램
  • 데이터의 분포를 시각화하는 데 사용되는 그래프
  • 연속된 데이터의 빈도를 막대 형태로 나타내어 데이터의 분포를 살펴볼 수 있음
    
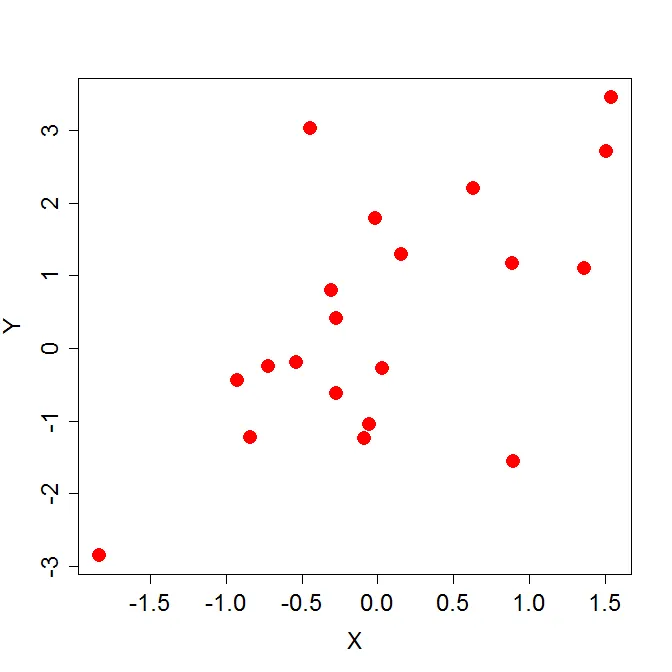
• 산점도
  • 두 변수 간의 관계를 시각화하는 데 사용되는 그래프
  • 각각의 데이터 포인트를 점으로 나타내어 변수 간의 상관 관계를 확인
  • 두 변수 간의 관계를 살펴보거나 이상치를 탐지하는 데 사용
    

통계 계산 함수

• 데이터 분석에서는 다양한 통계량을 계산해야 할 때가 있음
• 이를 위해 통계 계산 함수를 사용

import numpy as np

def calculate_mean(data):
    # 평균을 계산하는 함수
    return np.mean(data)

def calculate_std(data):
    # 표준편차를 계산하는 함수
    return np.std(data)

def calculate_correlation(x, y):
    # 상관 관계를 계산하는 함수
    return np.corrcoef(x, y)

표준편차와 상관관계

• 표준편차(Standard Deviation)
  • 데이터가 평균에서 얼마나 떨어져 있는지를 나타내는 측도
  • 분산의 제곱근으로 계산되며, 데이터 포인트와 평균 간의 거리의 제곱의 평균의 제곱근으로 정의
  • 데이터의 분포를 측정하는 데 널리 사용되며, 분산과 함께 데이터의 변동성을 나타내는 중요한 통계적 지표
    
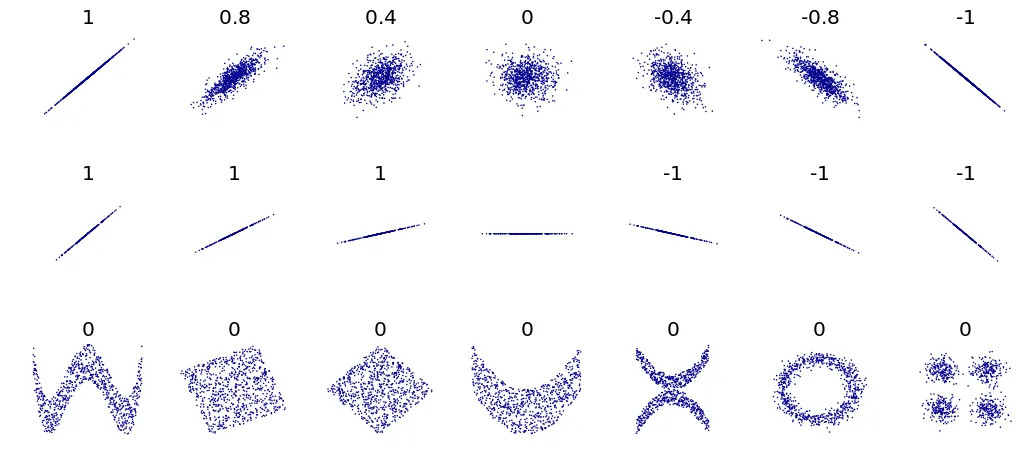
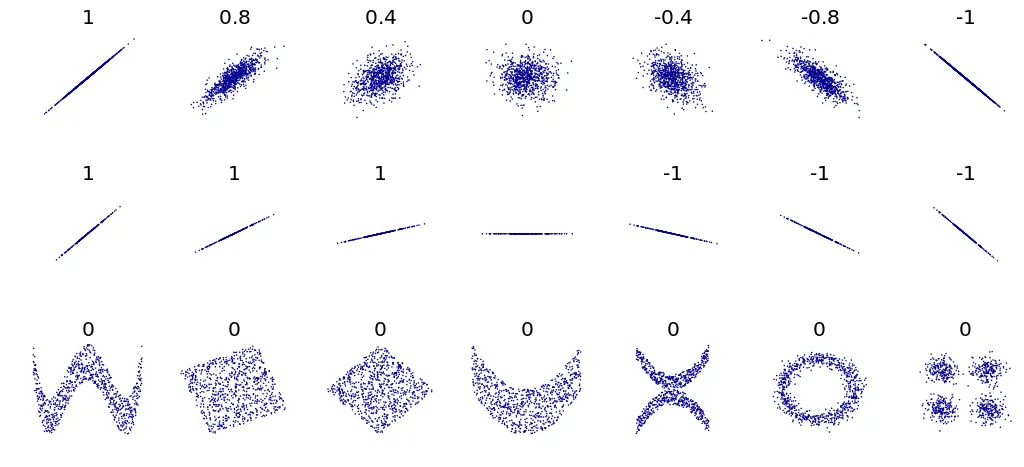
• 상관관계
  • 두 변수 간의 선형 관계의 강도와 방향을 나타내는 지표
  • -1부터 1까지의 값을 가짐
    → 1에 가까울수록 양의 선형 관계가 강함
    → -1에 가까울수록 음의 선형 관계가 강함
    → 0에 가까울수록 선형 관계가 약하거나 존재하지 않음을 의미
    

Quiz

• 평균과 분산 계산기
  • 주어진 데이터셋의 평균을 계산하는 함수를 작성하고 함수의 결과를 출력해 보세요!

data = [2, 4, 6, 8, 10]
def solution(data):
	return sum(data)/len(data)
result = solution(data)
print(f"평균: {result}")

다양한 경우의 수를 가진 정답이 나올 수 있기 때문에 혹여나 완전 똑같이 코딩하지 않았더라도 취지와 결과만 맞으면 모두 정답이라고 보시면 됩니다 🙂

def calculate_average(data):
    total = sum(data)
    length = len(data)
    average = total / length
    return average

data = [2, 4, 6, 8, 10]
result = calculate_average(data)
print("평균:", result)