https://www.acmicpc.net/problem/4673
문제
셀프 넘버는 1949년 인도 수학자 D.R. Kaprekar가 이름 붙였다. 양의 정수 n에 대해서 d(n)을 n과 n의 각 자리수를 더하는 함수라고 정의하자. 예를 들어, d(75) = 75+7+5 = 87이다.
양의 정수 n이 주어졌을 때, 이 수를 시작해서 n, d(n), d(d(n)), d(d(d(n))), ...과 같은 무한 수열을 만들 수 있다.
예를 들어, 33으로 시작한다면 다음 수는 33 + 3 + 3 = 39이고, 그 다음 수는 39 + 3 + 9 = 51, 다음 수는 51 + 5 + 1 = 57이다. 이런식으로 다음과 같은 수열을 만들 수 있다.
33, 39, 51, 57, 69, 84, 96, 111, 114, 120, 123, 129, 141, ...
n을 d(n)의 생성자라고 한다. 위의 수열에서 33은 39의 생성자이고, 39는 51의 생성자, 51은 57의 생성자이다. 생성자가 한 개보다 많은 경우도 있다. 예를 들어, 101은 생성자가 2개(91과 100) 있다.
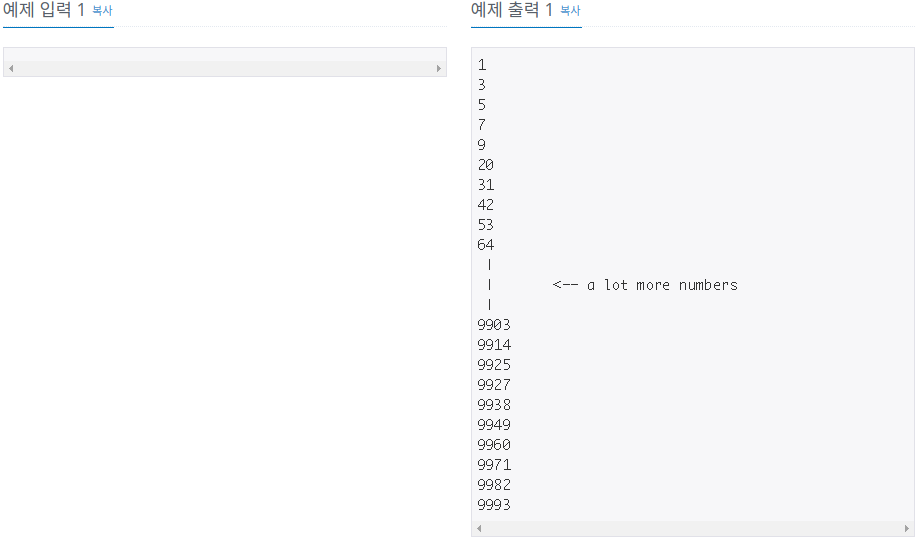
생성자가 없는 숫자를 셀프 넘버라고 한다. 100보다 작은 셀프 넘버는 총 13개가 있다. 1, 3, 5, 7, 9, 20, 31, 42, 53, 64, 75, 86, 97
10000보다 작거나 같은 셀프 넘버를 한 줄에 하나씩 출력하는 프로그램을 작성하시오.
입력
입력은 없다.
출력
10,000보다 작거나 같은 셀프 넘버를 한 줄에 하나씩 증가하는 순서로 출력한다.
풀이 1 (참고한 풀이)
def d(n):
return (n + sum(list(map(int, str(n)))))
not_self_number = []
for i in range(1, 10001):
if d(i) <= 10000:
not_self_number.append(d(i))
for j in range(1, 10001):
if j not in not_self_number:
print(j)월요일부터 고민한 문제고, 결국 풀지 못했다.
사실 몇 달 전에도 한창 알고리즘 문제를 풀다가, 이 문제에 막혀서 그만두었던 것 같다.
너무 안풀려서 오늘 결국 s직군님(https://rightbellboy.tistory.com/37)의 논리를 참고하였고,
구현만 내가 했다.
문제 마지막 줄에 적혀있듯이, 10000 이하의 셀프 넘버(생성자가 없는 수)를 찾아내어야 하는데
대체 이 셀프 넘버를 어떻게 구해야 하는건지 도통 생각이 나지 않았다.
내가 생각한 풀이는 1~10000 중 셀프 넘버가 아닌 수들을 not_self_number라는 list에 저장한 후,
출력할 때 1~10000에서 not_self_number에 포함된 수를 제외하고 출력하는 것이었다.
결국 이 논리가 맞긴 했지만, not_self_number를 구하지 못했다.
1~10000 전부 d(i)에 넣을 생각을 못하고, 계속 self number([1, 3, 5, 9, 20, 31 ... ])의 특징(공통점)을 찾으려 애썼다.
전부 부질없는 짓이었다..
배운 점
- 진짜 모르겠으면 주어진 범위의 수 전부를 때려 넣어보자.
- 특정 집단을 구해야 하는데, 구할 방법을 모르겠으면 전체 집단 - 나머지 집단(여집합)을 사용해 구해보자.