2609: 최대공약수와 최소공배수 - Python

문제

https://www.acmicpc.net/problem/2609

풀이 1: 중딩

a, b = map(int, input().split())
lst = []
div, gcd = 2, 1

while div <= min(a, b):
    if a % div == 0 and b % div == 0:
        a //= div
        b //= div
        lst.append(div)
    else:
        div += 1

for i in lst:
    gcd *= i

print(gcd)
print(a * b * gcd)

중학교 때 배우는 추억의 방법으로 풀어보았다.

풀이 2: math 모듈

import math

a, b = map(int, input().split())
gcd = math.gcd(a, b)
print(gcd)
print(a * b // gcd)

Python 내장 모듈인 math에서 gcd() 함수를 사용해 간단히 구할 수 있다.
또는

import math

a, b = map(int, input().split())
print(math.gcd(a, b))
print(math.lcm(a, b))

최소공배수를 구하는 math.lcm()를 사용할 수도 있다.

풀이 3: 유클리드 호제법

def GCD(x, y):
    while y:
        x, y = y, x % y
    return x

a, b = map(int, input().split())
gcd = GCD(a, b)
print(gcd)
print(a * b // gcd)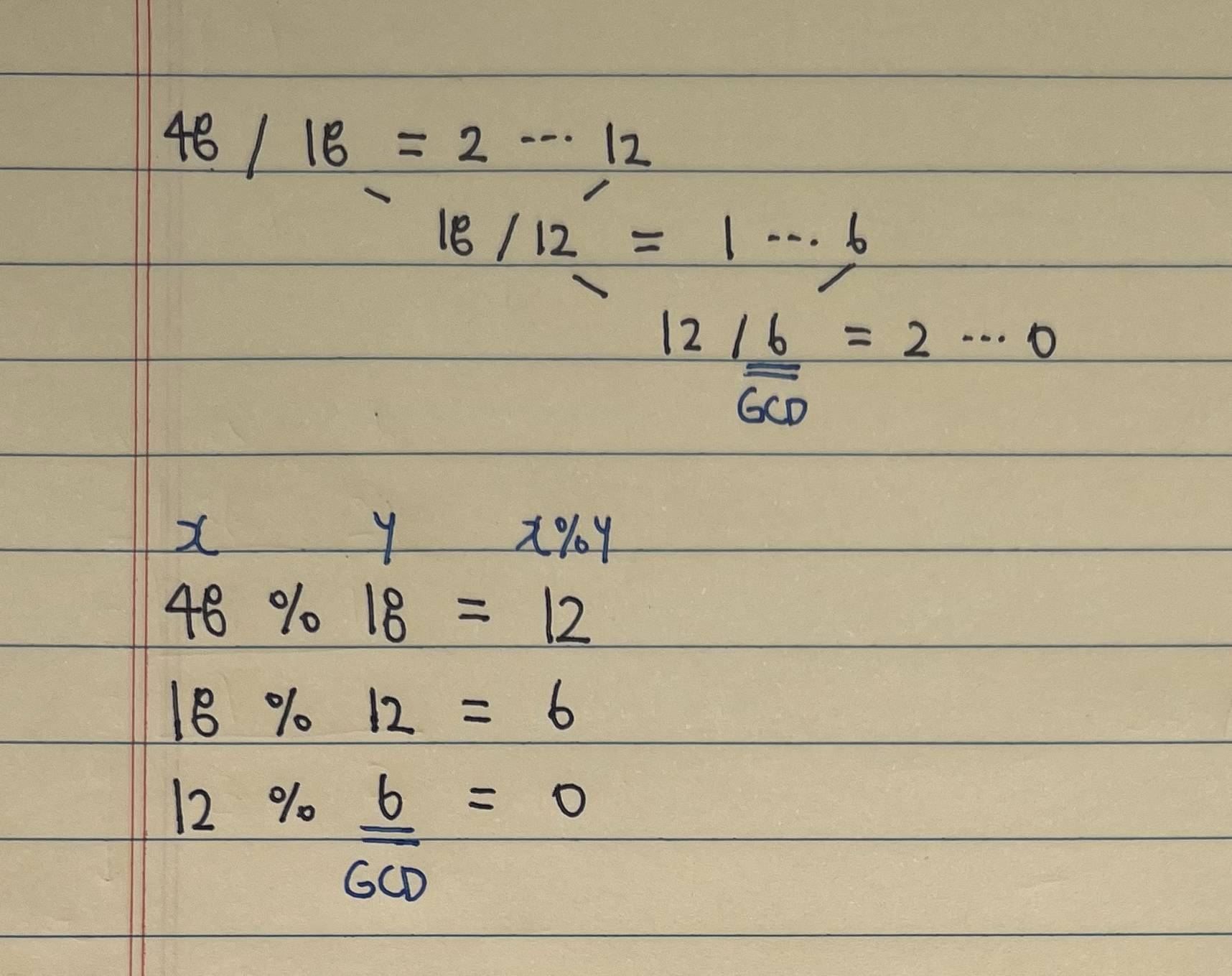

유클리드 호제법을 이용해 최대공약수를 구할 수 있다.
GPT를 조금 참고했다.

---

오늘의 교훈

• 최대공약수를 구할 때는 유클리드 호제법을 이용하자.
• 최소공배수는 수1 * 수2 // 최대공약수로 구할 수 있다.
• 아래의 약자는 기억하자.
  • 최대공약수 = Greatest Common Divisor = GCD
  • 최소공배수 = Least Common Multiple = LCM