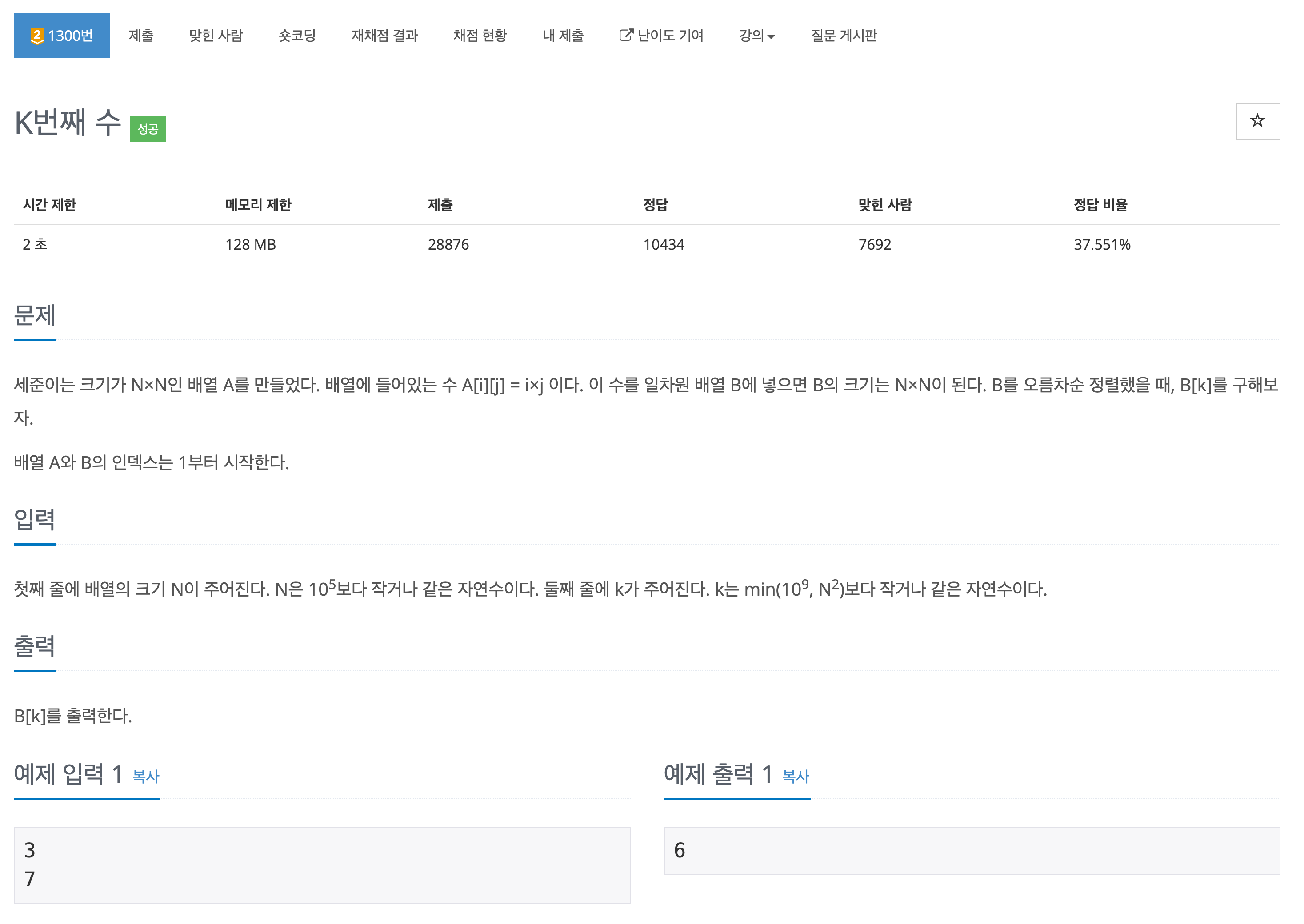
문제

풀이 과정

이분 탐색 문제.
풀이 방식은 다음과 같다.
우선 idx는 1부터 시작하기 때문에 어떤 수 arr[k] 는 k 보다 작거나 같을 수 밖에 없다. 또한 해당 배열에는 arr[k] 보다 작은 값이 k개 있다고 판단 할 수 있다.
해당 임의의 값 x 보다 작은 수를 판단하는 것은 x를 idx 로 나눈 몫이 된다. 해당 배열은 오름차순 정렬이 되어있기 땜누에, 모두 임의의 값 x 보다 작은 값이 된다.

이분 탐색을 시작하여, 전체 x 보다 작은 수가 K 개 보다 크다는 것은 일단 범위 반경 안에, arr[k] 보다 작거나 같은 값들이 모두 포함되어 있다고 할 수 있다. 따라서 더 근접한 확인을 위해 ed 값을 줄이자.
반대로 전체 x 보다 작은 수가 K 개 보다 작다는 것은 현재 arr[k] 보다 작거나 같은 값이 모두 포함되어 있지 않다는 것을 의미하므로, 따라서 st 값을 높여주면 된다.

upperBound, lowerBound 에 대해 따로 공부할 필요가 있겠다.

정답

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class Main {
    static int N, K;
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        K = Integer.parseInt(br.readLine());

        int st = 1;
        int ed = K;
        while (st<ed) {
            int mid = (st + ed) / 2;
            int cnt = 0;
            for (int i = 1; i <= N; i++) cnt += Math.min(N, mid/i);
            if (cnt>=K) ed = mid;
            else st = mid+1;
        }
        System.out.println(ed);
    }
}