BOJ 3474 : 교수가 된 현우

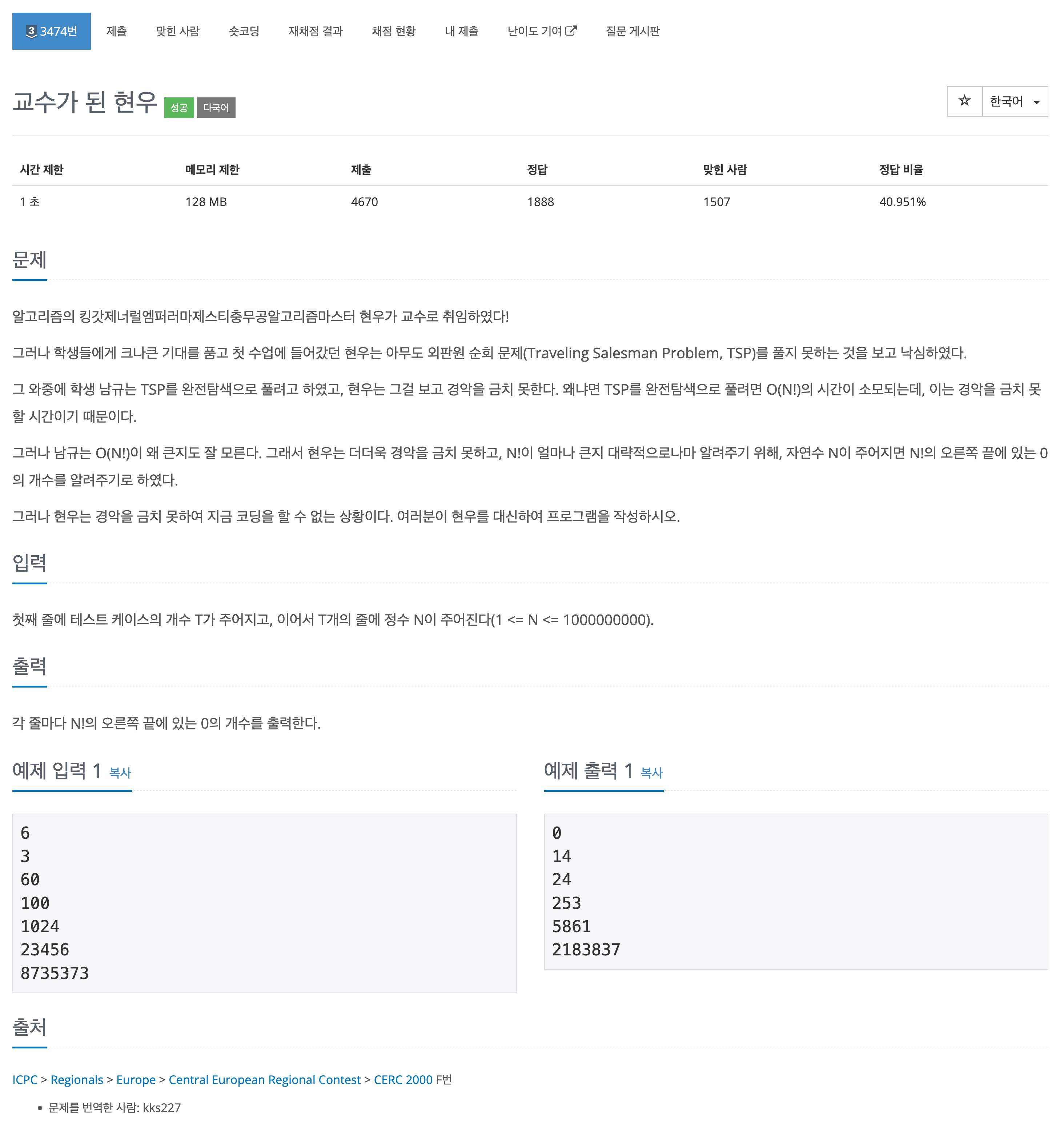
풀이 요약

그리디 문제

풀이 상세

1. 임의의 수에 대한 팩토리얼에 대하여, 오른쪽 끝이 $0$ 으로 채워진 갯수는 $10$ 이 곱해질 때 마다 생성되는 것이며, 이러한 $10$ 을 곱하는 경우가 총 몇개인지 찾는 문제이다.

2. $10$ 을 소인수 분해 하면 $2^1 * 5^1$ 로 표현이 가능하며, $10^i$ 는 $2^i*5^i$ 로 치환할 수 있다.

3. 즉, 해당 팩토리얼의 전체 값을 소인수 분해로 나누었을 때, $2$ 의 갯수와 $5$ 의 갯수 가운데, 더 작은 갯수를 반환하면 된다.

4. 허나, 기본적으로 어떠한 수에서든 $5$ 의 갯수 가 $2$ 의 갯수 보다 많은 경우는 없기 때문에, $5$ 의 갯수만 구하면 된다.

5. 모든 팩토리얼 값은 기본 숫자 타입을 아득히 넘기 때문에, 팩토리얼을 구하지 않은 상태에서 $5$ 의 갯수를 찾아야 한다.

6. $5!$ 로 예를 들어보자. 다음과 같은 식을 통해 팩토리얼의 해당 배수의 갯수를 구할 수 있다.

   		1 2 3 4 5
   2의 배수    1   1  
   4의 배수        1    
   
   5! = 120 => 2^3*3*5
   5의 2의 갯수는 5/2 + 5/4 = 3

배운점

• C++ 시, 그냥 입력값을 받으면 시간 초과가 나온다. 꼭 ios::sync_with_stdio(0) , cin.tie(0) 를 작성해주자.
• 식을 찾기까지가 별의별 생각을 다했는데, 결국 최초의 식이 정답에 제일 근접했다. 이럴 때가 제일 허탕한 거 같다.

#include <iostream>
using namespace std;
int N, curr_num;

int solve() {
    int num = 0;
    for(int i=5; i<=curr_num; i*=5) num += curr_num/i;
    return num;
}

void output(int ans) {
    cout << ans << "\n";
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> N;
    for (int i = 0; i < N; i++) {
        cin >> curr_num;
        int ans = solve();
        output(ans);
    }
}