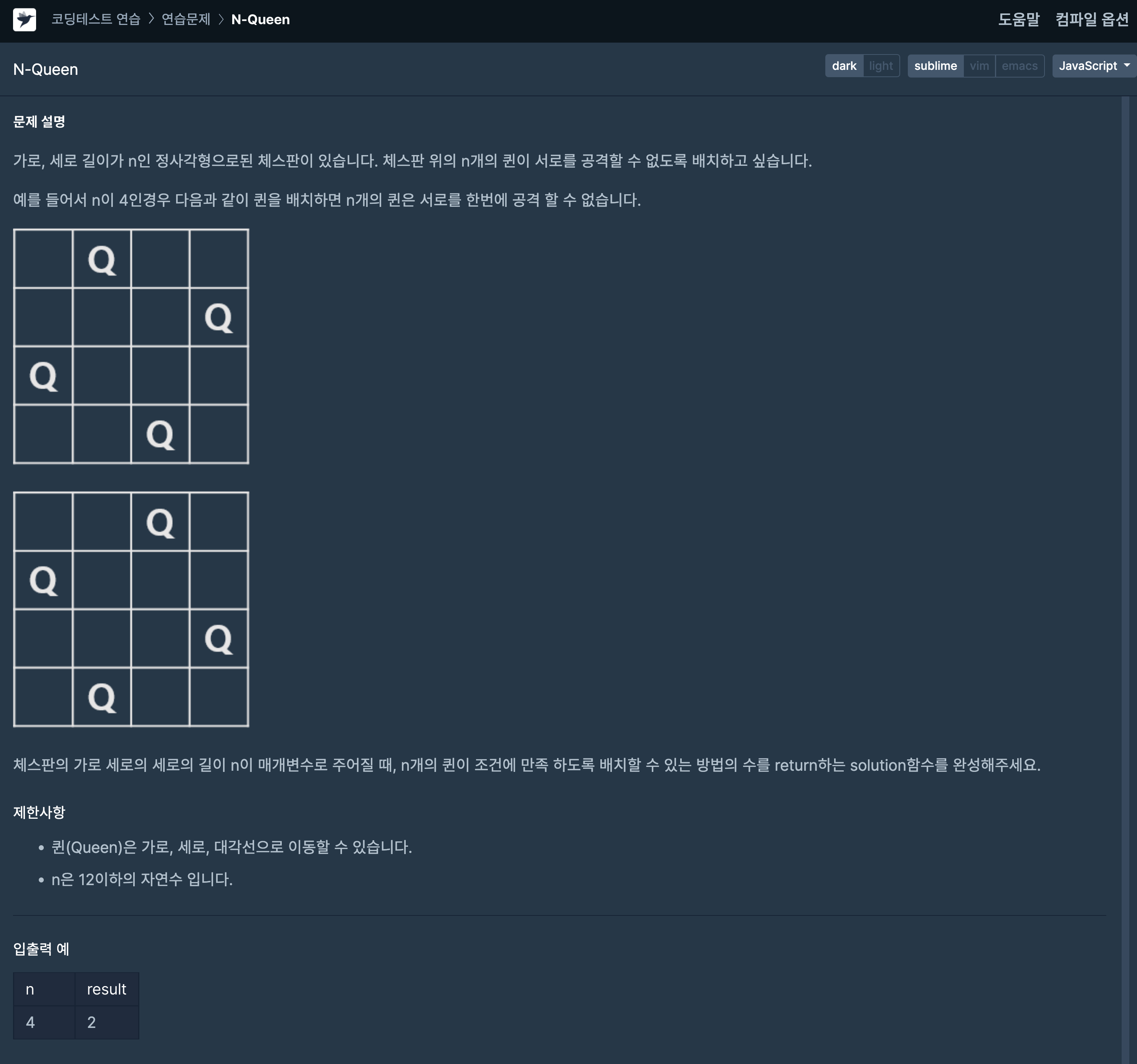
문제

풀이 과정

백트래킹 대표 문제.
갑자기 N-Queen 어떻게 풀었지 기억이 안나 한번 시도해보았다.
체스의 퀸은 상하좌우, 모든 대각선을 자유롭게 움직일 수 있다. 따라서 다음 퀸이 놓이는 좌표는 이전 퀸으로부터 행, 열이 같으면 안되며, 대각선 방향도 같아서는 안된다.

먼저 일차원 배열에, 각각의 퀸의 $x$ 좌표를 넣을 거다. DFS() 로 탐색하기 때문에 depth 곧 $y$ 좌표가 되어 열이 겹칠일은 없을 것이다. 일차원 배열 초깃값은 최대 범위에서 절대 도달할 수 없는 값을 넣어두었다. (999)
만약 해당 배열의 인덱스가 999 라면 해당 열에 아직 퀸이 놓여있지 않음을 의미한다.

대각선의 경우에는 테케를 직접 만들어 찾아보았는데 (0,1) 에 퀸이 놓이면 다음 퀸은 (1,0), (1,2), (2,3) 좌표에 놓일 수 없다. 이전 퀸의 좌표와 다음 퀸의 좌표가 대각선을 이루는 공식은 다음과 같다.

$|prev.y-next.y| == |prev.x-next.x|$

이를 기반으로 백트래킹을 수행하면 정답이 나온다.

정답

let ans = 0;
let arr;
function solution(n) {
  arr = new Array(n).fill(999);
  DFS(n,0)
  return ans;
}

function DFS(n, r) {
  if(r>=n) {
    ans++;
    return;
  }

  for(let c=0; c<n; c++) {
    if(check1(c) && check2(r,c)) {
      arr[c] = r;
      DFS(n, r+1);  
      arr[c] = 999;  
    }
  }
}

function check1(c) {
  return arr[c] == 999;
}

function check2(r,c) {
  for(let i=0; i<arr.length; i++) {
    if(Math.abs(r-arr[i]) == Math.abs(c-i)) {
      return false;
    };
  }
  return true;
}