버블정렬, $O(N^2)$

소개

인접한 두 원소끼리 비교하여 정렬을 진행하는 알고리즘이다.

정렬 과정

첫 번째 자료와 두 번째 자료를, 두 번째 자료와 세 번째 자료를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1)번째 자료와 마지막 자료를 비교하여 교환하면서 자료를 정렬한다.

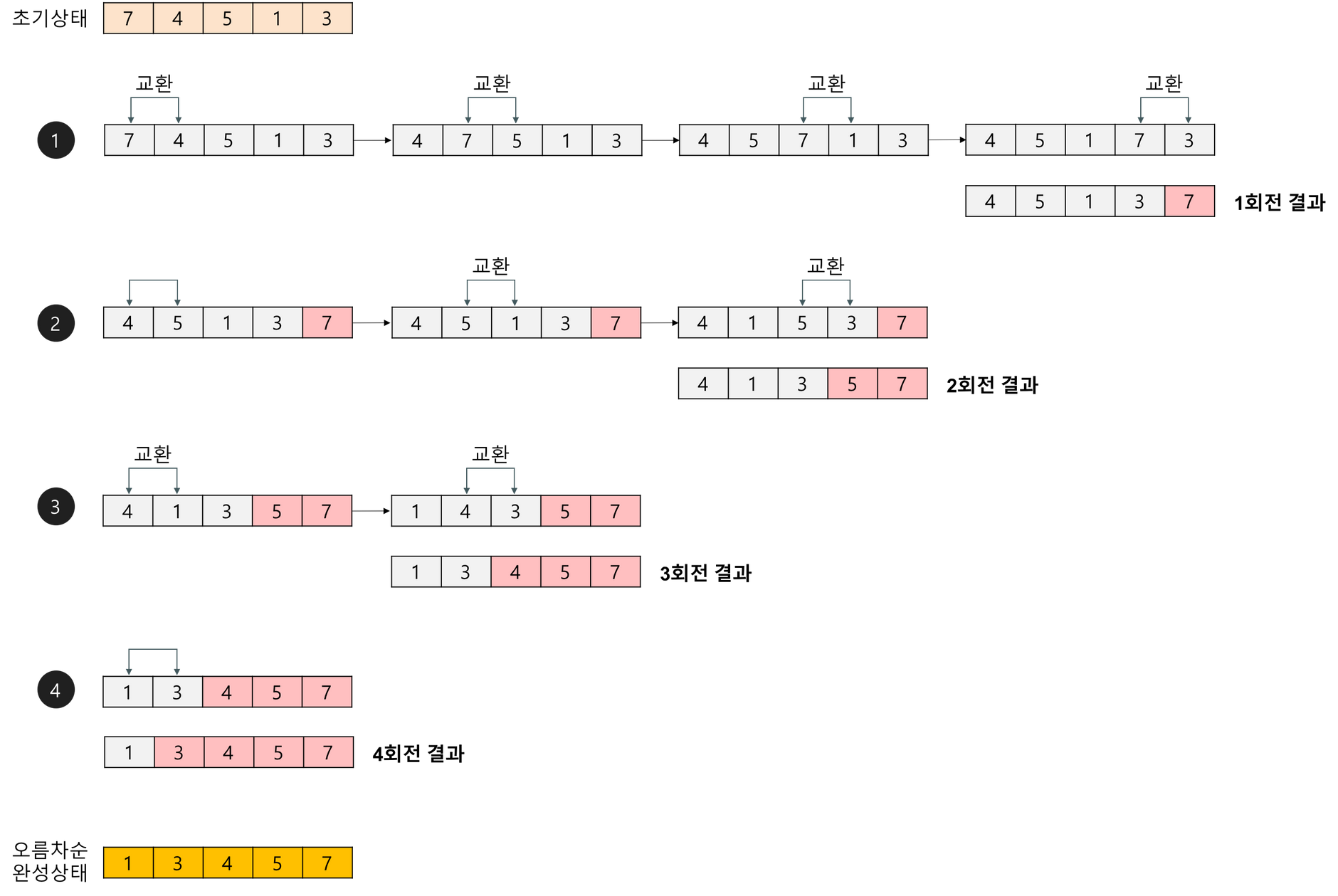
비고

동일한 값에 기존 순서가 유지되는 안정 정렬 이면서, 추가적인 메모리가 더 필요하지 않은 제자리 정렬(in-place sort) 이다.

선택정렬, $O(N^2)$

소개

원소를 넣을 위치를 지정하고, 그 위치에 어떠한 원소를 넣을지 선택하는 알고리즘이다.

정렬 과정

현재 인덱스를 시작으로 최소값 혹은 최댓값을 탐색하여, 현재 인덱스의 값과 교체한다. 이후 다음 인덱스에서 동일한 과정을 반복하여 마지막 인덱스 - 1 까지 진행한다.

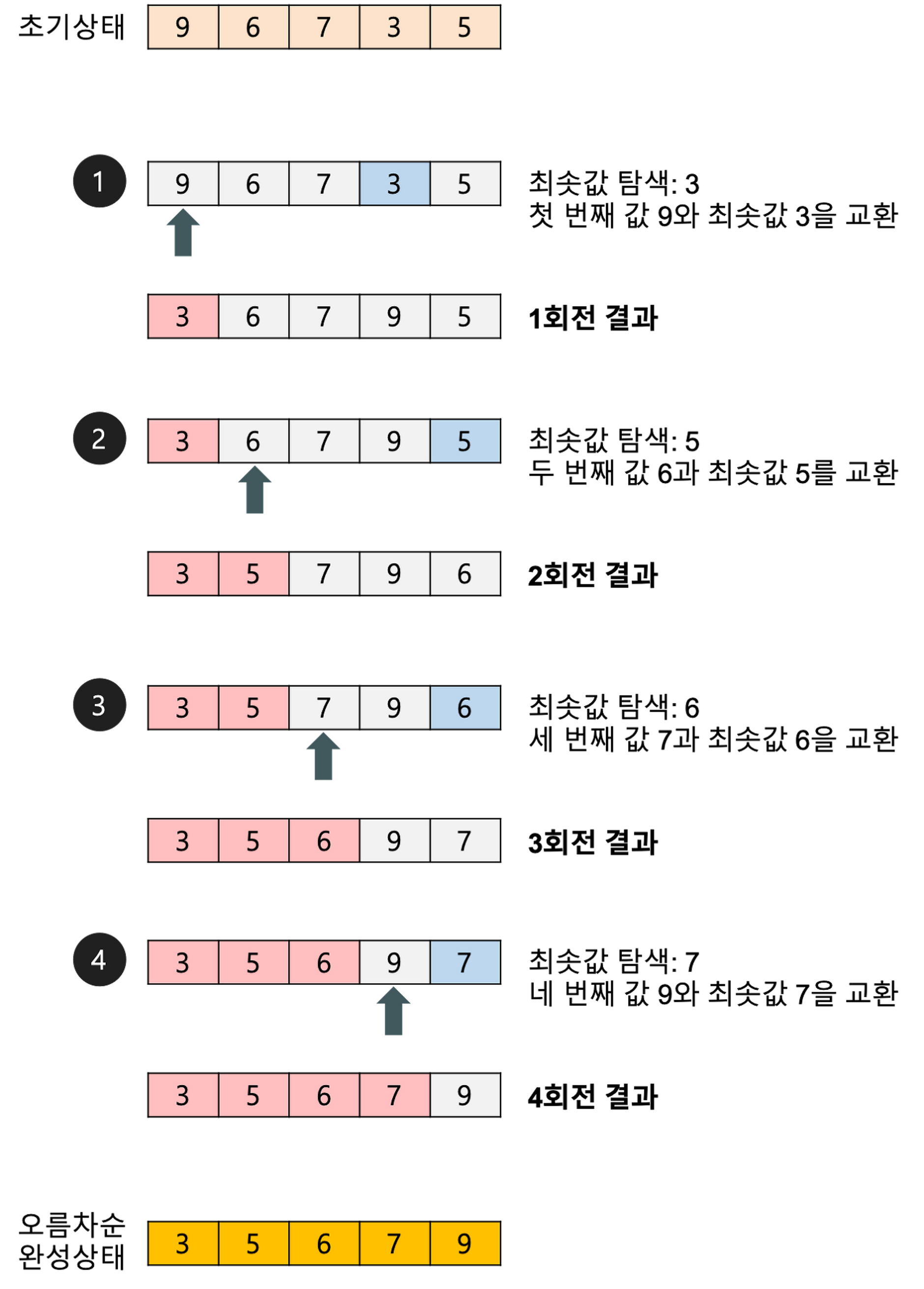
비고

시간 복잡도는 버블 정렬과 동일하지만, 버블 정렬의 경우 매 과정마다 최대 $N$ 번의 swap 과정이 진행되는 것 대비, 선택정렬은 단 한번의 swap 만 발생한다는 점에서 버블정렬보다 더 적은 리소스를 사용한다. (더 빠를 수 있다)

동일한 값에 기존 순서가 보장되지 않는 불안정 정렬을 이루며, 추가적인 저장 메모리가 더 필요하지 않은 제자리 정렬(in-place sort) 이다.

카운팅(계수) 정렬, $O(N+K)$

소개

카운팅을 활용한 정렬 알고리즘으로, 주어진 조건에만 부합한다면 가장 빠른 정렬 알고리즘이다. 기존 비교 기반의 알고리즘이 아닌, 원소 값의 누적합을 기반으로, 배열 정렬을 수행한다.

정렬 과정

카운팅 배열을 생성하여, 각 원소의 숫자가 몇번 등장했는지를 배열에 저장한 후 누적합을 진행한다. 누적합의 값에 따라 이후 배치가 이루어지고, 배치마다 각 인덱스의 값을 -1 씩 지운다. 이과정을 반복한다.

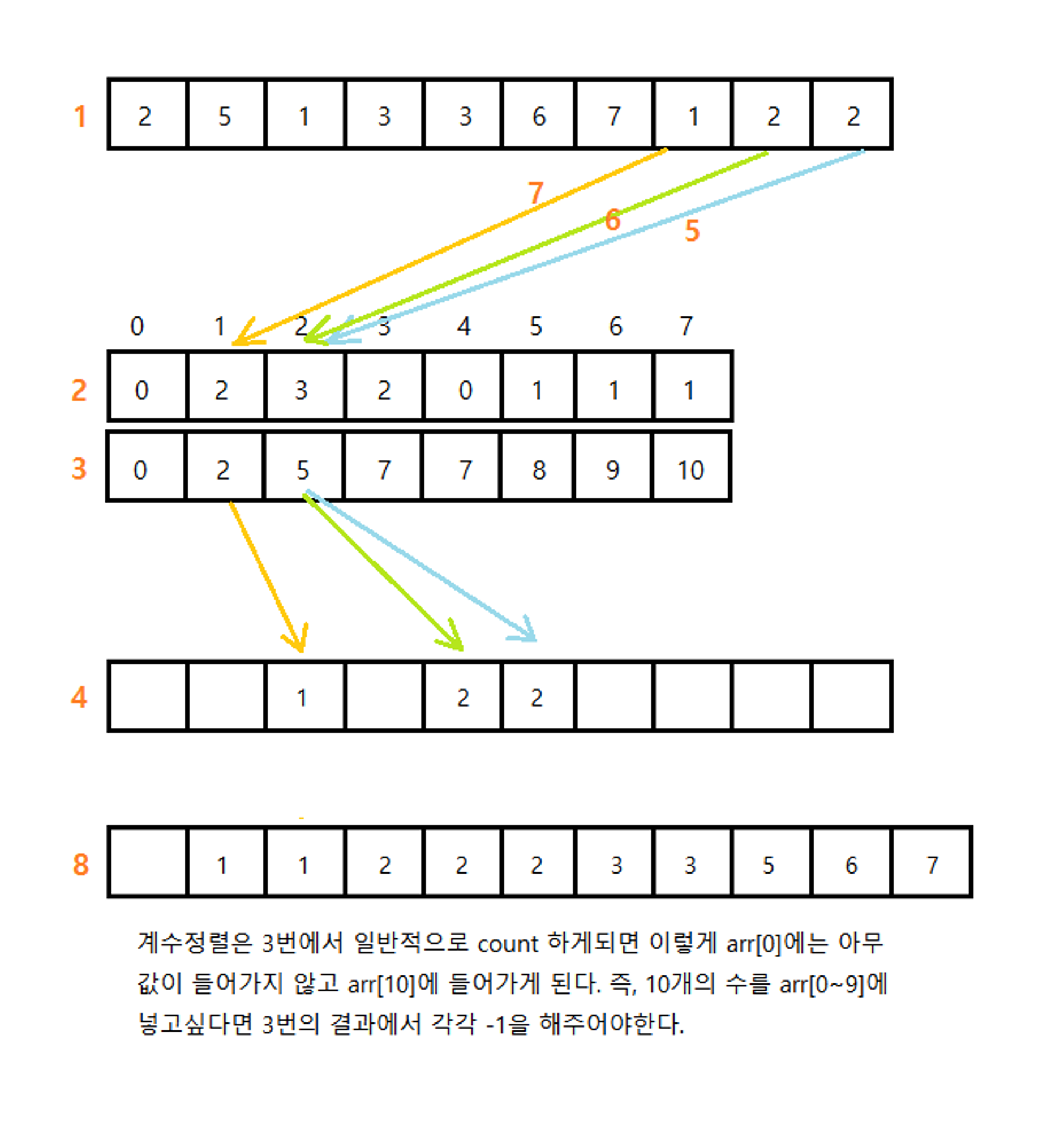
비고

카운팅 정렬의 경우 최댓값이 100만 이내여야 하며(더 크면 배열을 생성하기 어렵기 때문), 최솟값과 최댓값의 범위가 비교적 적어야 한다. 범위가 큰 경우에는 사용되지 않는 인덱스가 많아 메모리 낭비가 심하기 때문이다..

동일한 값에 기존 순서가 유지되는 안정 정렬을 이루며, 추가적인 메모리가 확보되어야 하는 비제자리 정렬 (NOT in place sort) 이다.

삽입정렬, $O(N^2)$

소개

앞의 원소들과 비교하여 삽입할 위치를 지정하여 해당 원소를 그 자리에 삽입하는 정렬 알고리즘이다.

정렬 과정

두번째 원소를 시작으로, 이전 위치에 있는 원소들을 비교한다. 타겟이 되는 숫자가 이전 위치에 있던 원소보다 작다면 타겟이 되는 숫자를 다음 인덱스로 미룬다. 타켓이 더 큰 경우가 나타나면 반복문을 종료하고 해당 이전 위치의 원소의 다음 자리에 타켓 숫자를 배치한다.

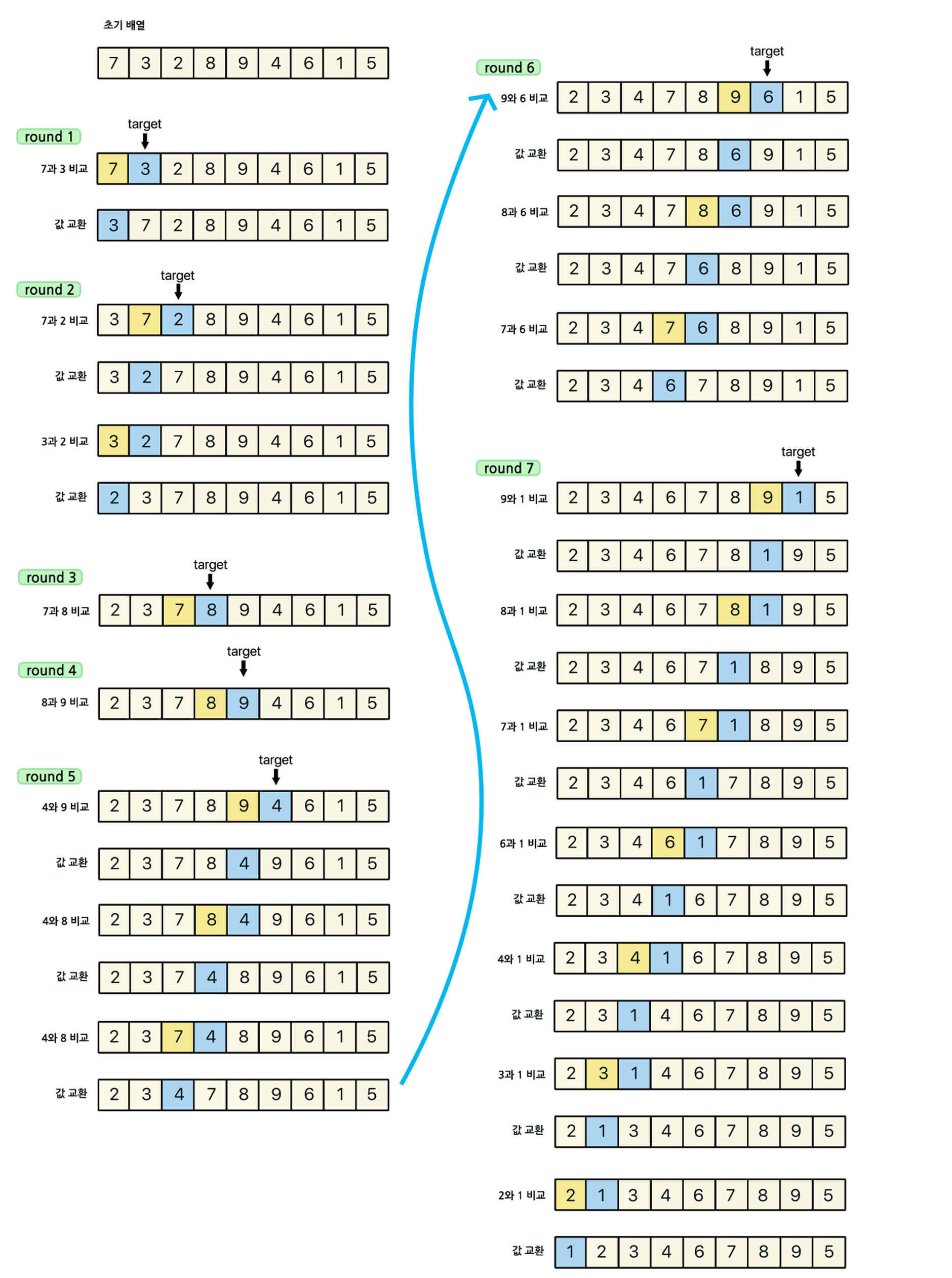
비고

동일한 값에 기존 순서가 유지되는 안정 정렬 이면서, 추가적인 메모리가 더 필요하지 않은 제자리 정렬(in-place sort) 이다. 버블정렬과 유사하게 계속해서 자리 이동이 진행되기 때문에 연산비용이 비교적 크다.

힙정렬, $O(nlogn)$

소개

완전 이진트리 기반의 우선순위 큐를 위한 정렬 알고리즘이다.

정렬 과정 (최대힙 정렬)

최대 값을 루트 노드로 하여 자식 노드로 갈수록 더 작은 값이 배치되는 배열을 만든다. 루트 인덱스를 1 이라 하고 자식 노드에 해당하는 임의의 인덱스를 $n$ 이라 한다고 가정했을 때, 관련 노드의 배열 인덱스는 다음과 같이 표현할 수 있다.

• 부모 인덱스 : $n/2$
• 왼쪽 자식 인덱스 : $n∗2$
• 오른쪽 자식 인덱스 : $n∗2+1$

Heapify

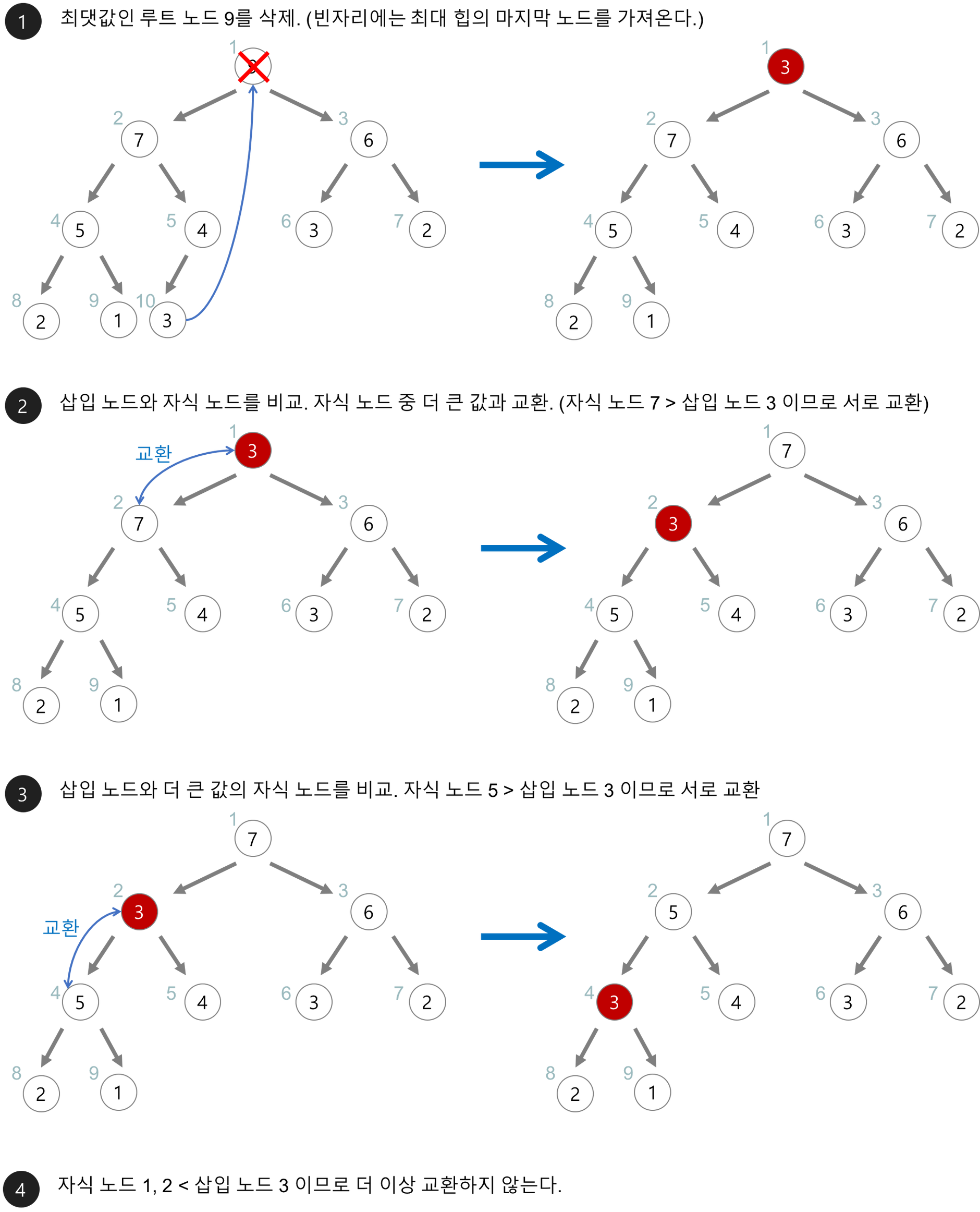
자식과 부모의 대소비교를 통해, 노드의 위치를 스왑하는 과정이다. 해당 원리는 새로운 노드를 삽입하는 경우와 노드를 반환(삭제) 하는 경우 일어난다.

• 삽입 : 삽입하는 값을 먼저, 배열의 마지막 인덱스로 추가한다. 삽입한 리프 노드를 기준으로, 부모 노드와 대소비교를 통해 조건에 해당하는 경우, 부모-자식의 관계를 스왑한다.
• 삭제 : 루트 노드의 값 (최소 혹은 최대) 을 제거하고, 맨 마지막 데이터를 루트노드로 옮긴 후, 부모 노드와 대소비교를 통해 조건에 해당하는 경우, 부모-자식 관계를 스왑한다.

비고

동일한 값에 기존 순서가 유지되지 않는 불안정 정렬 이면서, 상황에 따라 배열의 길이가 늘거나 줄어드는 비제자리 정렬(NOT in-place sort) 이다.

병합정렬, $O(nlogn)$

소개

분할정복 기법과 재귀 알고리즘을 이용한 정렬 알고리즘이다.

정렬과정

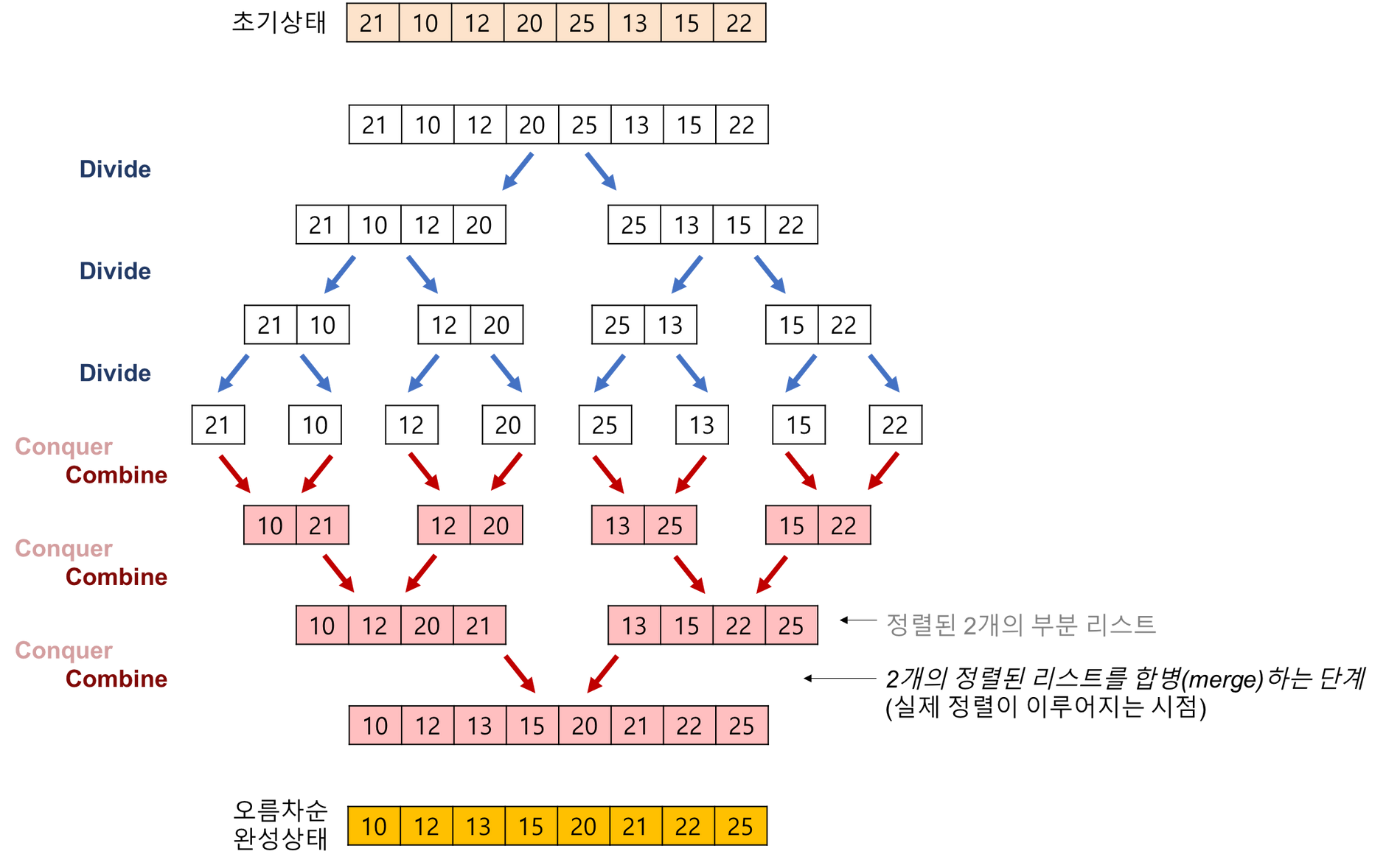
주어진 원소가 하나 밖에 남지 않을 때 까지 지속적으로 반으로 쪼갠 후 쪼개진 배열끼리 먼저 정렬하여 다시 원래 크기로 합치는 과정을 반복한다.

비고

동일한 값에 기존 순서가 유지되는 안정 정렬 이면서, 분할된 배열 값을 저장하기 위한 추가적인 메모리를 사용하는 비제자리 정렬에 해당한다. 배열 값의 이동이 매우 많다는 점에서 배열의 사이즈가 클수록 연산 비용이 기하급수적으로 증가한다.

퀵정렬, $O(nlogn)$

소개

분할정복 기반의 알고리즘으로, 피벗 기반의 비교 정렬 알고리즘이다. 평균 속도가 빠른 편이라, 실제 프로그래밍 언어의 정렬 API에 많이 사용된다.

정렬 과정

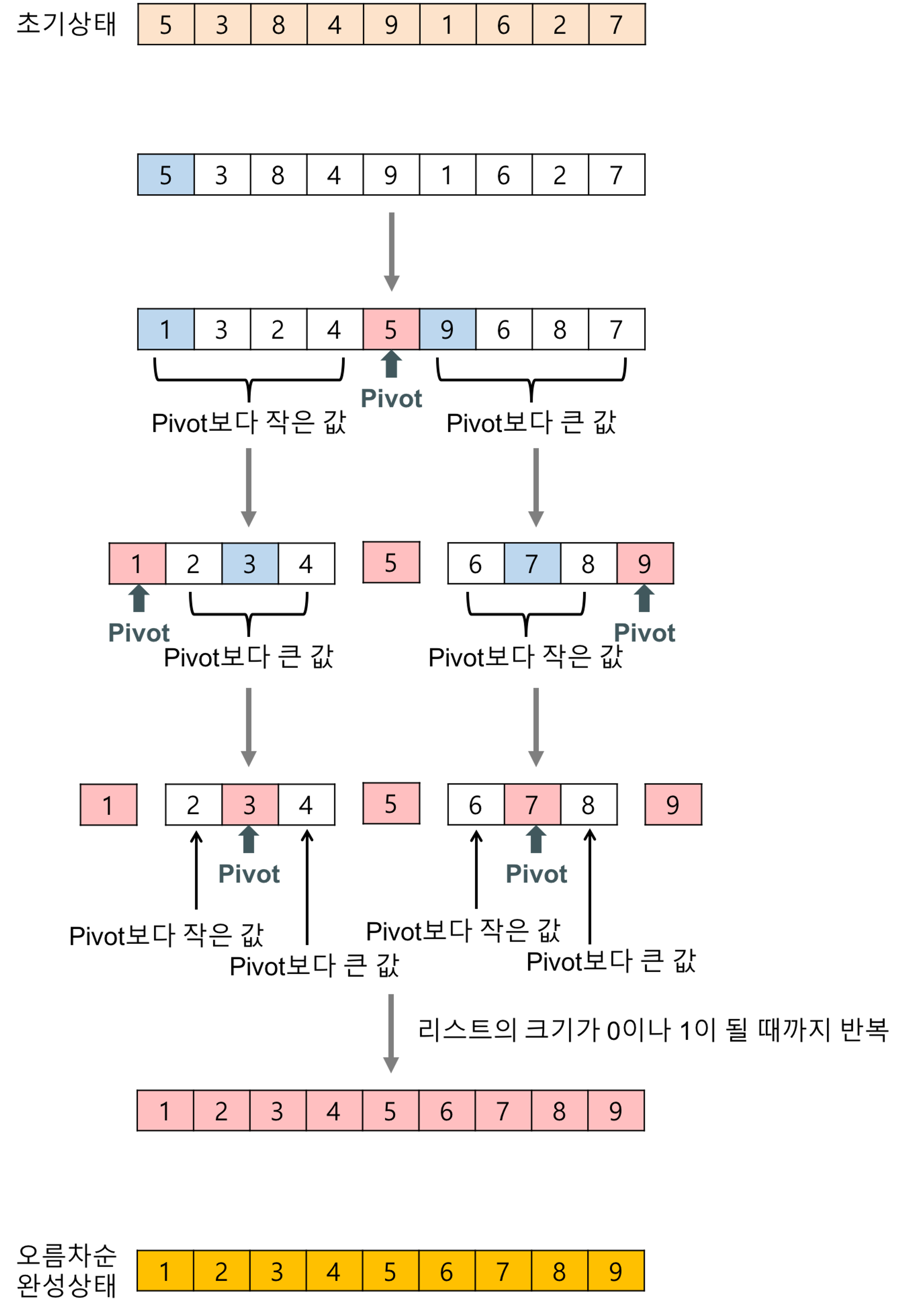
피벗 데이터를 선택하여 피벗 데이터 대비 작은 데이터의 묶음과 큰 데이터의 묶음을 만든 후, 작은 데이터의 묶음과 큰 데이터의 묶음의 피벗 데이터를 선택하여 해당 과정을 반복한다.

비고

동일한 값에 기존 순서가 유지되지 않는 불안정 정렬 이면서, 추가적인 메모리가 더 필요하지 않은 제자리 정렬(in-place sort) 이다.

불필요한 데이터의 이동을 줄이고, 한 번 결정된 피벗들의 경우 추후 연산에서 제외되기 때문에, 시간복잡도가 $O(nlogn)$ 의 알고리즘 가운데 가장 빠르다. 피벗 선택 시 균등하게 분할되지 않는 경우 오히려 수행시간이 올라갈 수 있다. (최대 $O(N^2)$)

위상정렬, $O(V+E)$

소개

DAG (사이클이 없는 방향 그래프) 기반의 정렬 알고리즘. 노드 간 진입차수를 통해 일의 순서를 정렬한다.

정렬과정

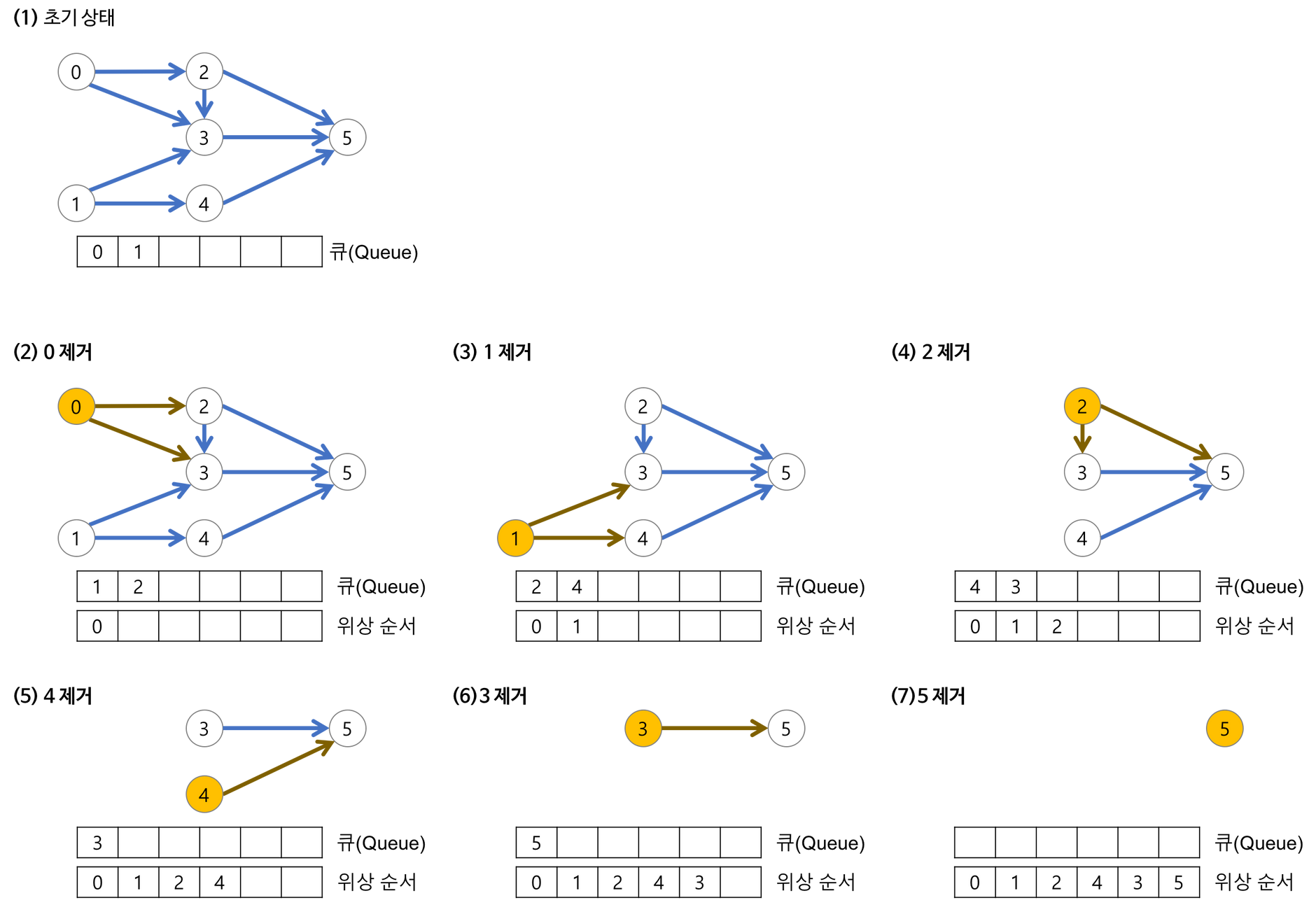
진입차수가 0인 노드를 큐에 넣는다. 이때 진입차수가 0이라는 뜻은 해당 업무를 위한 선행작업이 없거나 모두 끝마친 상태를 의미한다. 해당 노드와 연결된 간선을 통해 다음 노드로 이동하며, 다음 노드에 대한 진입 차수도 1개씩 제거한다. 만약 다음 노드의 진입 차수도 0이 된다면, 큐에 넣어 탐색과정을 반복한다.

비고

선행 및 후행작업이 있고, 해당 입력값이 사이클이 없는 그래프를 이루는 경우에만 사용이 가능하다. 특히 쉬운 것부터 빠르게 해결하는 최적해 방식의 문제는 대부분 위상정렬 문제에 해당하는 듯 하다.

참고
[알고리즘] 버블 정렬(bubble sort)이란 - Heee's Development Blog
Counting Sort : 계수 정렬
자바 [JAVA] - 카운팅 정렬 (Counting Sort / 계수 정렬)
자바 [JAVA] - 삽입 정렬 (Insertion Sort)
[알고리즘] 퀵 정렬(quick sort)이란 - Heee's Development Blog
25. 위상 정렬(Topology Sort)
퀵 정렬 (Quick sort) 쉽게 알기
[알고리즘] 위상 정렬(Topological Sort)이란 - Heee's Development Blog