Binary Search Tree
Definition: a hierarchical data structure (tree) in which each node has at most 2 children
- A node's left subtree has values less than the node's value
- A node's right subtree has values greater than the node's value
BST enables efficient search for values since all values are sorted into the tree.
However, upon insertion and deletion operations, the tree must rebalance each time, resulting in inefficient performances.
M-Way Search Tree
Multi-level indexing attempts to manage multiple indexes, which appeared with larger datasets.
- Another level of indexing: The new index stores a pointer to each block of the first level index table
- uses a hierarchy of index structures to efficiently access data
- keeps a tree balanced by storing more than 1 key per node
- Hence, a tree will always be perfect (but not necessarily binary)
M-way search tree is a common multi-level indexing structure that allows more than two children per node, more specifically M-1 to 2M-1 children (M >= 1).
Unfortunately, this restriction in number of trees means that the tree requires restructuring upon insertion and deletion operations.
B-tree
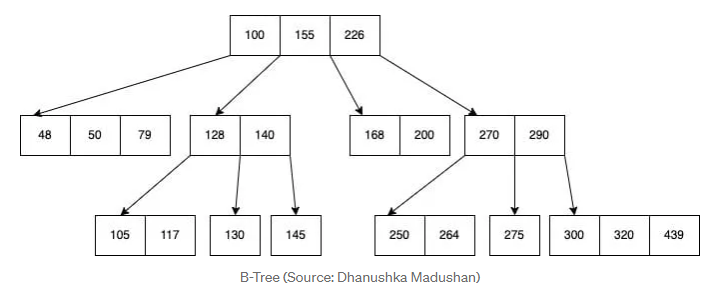
A B-tree addresses the shortcomings of M-way search trees in cases of frequent insertions and deletions.
Definition: a balanced tree structure that
- balanced height: all leaf nodes are at the same level
- self-balancing
- enables predictable and efficient search operations
- provides sorted data
- allows searches, sequential access, insertions/deletions in sorted order
- maintains a BST quality of having a node's left subtree as values less than node and its right subtree as values greater than node
- but allows more than 2 children
Downsides
- requires additional storage space for creating and maintaining a B-tree
- restructuring a B-tree upon insertions and deletions may cause performance issues
B+ tree
The key difference between a B-tree and a B+ tree is how data is stored. The fact that B-trees store data in internal and leaf nodes whereas B+ trees store data only in leaf nodes result in the following differences as well.
-
Data pointer storage
- All internal and leaf nodesof B-trees have data pointers
- Only leaf nodes of B+trees have data pointers
-
Redundant keys
- B-tree does not have duplicates of keys
- B+tree has duplicate keys since all nodes are present at a leaf node.
-
Search complexity
- B+ tree has simplified search process because all data is found in leaf nodes
- B+ tree allows sequential search due to linked list nature of leaf nodes
-
Range queries
- Leaf nodes of a B+ tree are linearly connected, improving range-query performances
-
Balancing
- Leaf-only data structures allows B+ trees to be more balanced
References:
