문제 바로가기

https://www.acmicpc.net/problem/1541

문제 소개 및 재정의

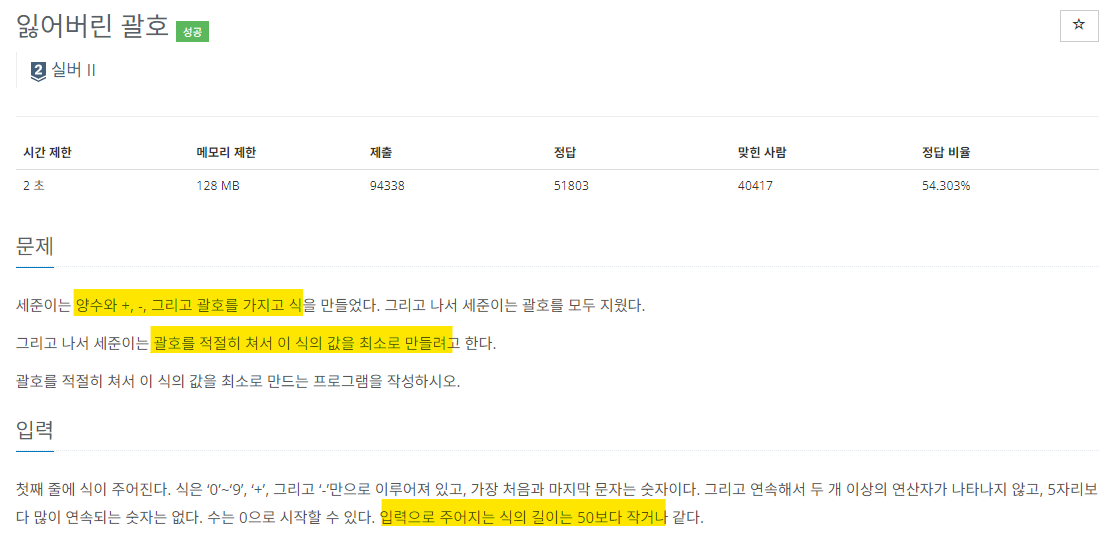
+와 - 연산만 있는 식의 값을 최소화 하시오.
피연산자는 모두 양수이고, 임의대로 괄호를 추가할수 있다.

문제 패턴

처음에 두가지의 생각이 들었다.

• 괄호를 치는 모든 경우의 수를 구해서 완전탐색으로 푸는 것
• 최소값이 되는 규칙을 찾아서 푸는것

어떻게 풀까? - 완전 탐색

포인트

괄호를 치는 것을 구현하는게 너무 어려웠다.
고민 끝에 아래와 같은 결론을 얻었다.

• 괄호를 친다. <=> 연산 순서를 결정한다.
• 연산자에 번호를 매긴다음에 순열을 만든다 => 연산 순서를 결정한다
• 연산자에 번호를 매긴다음에 순열을 만든다 => 괄호를 친다

따라서 연산자의 개수를 길이로 가지는 순열을 만들었다.
그런데 문제에서 최악의 경우 연산자의 개수는 24개이다.
시간복잡도가 24!인 것인데....
순열의 시간복잡도를 착각하지 않았더라면 시간복잡도가 너무 커서.
완전탐색 풀이를 포기했을것 같다.
이런 말을 하는 이유는 착각했기 때문이다.

구현 시 어려웠던 점.
연산할때마다 피연산자는 연산결과값으로 덩어리로 뭉치게됨.

하나로 합쳐졌으니 인덱스를 삭제해볼까?
그러면 피연산자리스트의 인덱스와 연산자 인덱스의 조화가 어그러진다.
그리고 리스트의 삭제 연산은 비용이 비싸서 다른 방법을 생각해봤다.

연산할때마다 나온 결과값을, 같은 덩어리로 합쳐진 피연산자 위치에 마스킹 하는 것이다.
그러면 계산이 정확해진다.
그러기 위해서는 같은 덩어리를 찾기 위해서 DFS를 할 필요가 있다.
DFS를 하기 위해서 현재 연산이 몇번째(i)로 하는중인지 그 값으로 방문배열 상에서의 덩어리들을 마스킹 할 필요가 있었다.
그러면 연산을 처음하는 피연산자는 바로 i로 저장하고.
아니라면 DFS로 자기랑 같은 덩어리 번호인것들만 타고가면서 i로 저장한다. 그럼 또 같은 덩어리가 기록된다.

하지만 다시 생각해보니 연산자의 크기가 최대 24이므로 그냥 리스트에서 인덱스를 삭제해도 될것 같다.
피연산자리스트에서 리스트를 삭제할때, 해당 위치의 연산자 리스트의 인덱스도 삭제해주는 방식으로.
시간이 많이 소요되지 않는것 같아서 좋다.
위의 방법은 너무 구현하기 힘들다.

샘플 테케는 잘 통과했지만, 실제 채점에서는 1% 이후에 시간초과가 발생했다.

코드

// 어디까지 마스킹할지가 너무 어려운데영....
import java.io.*;
import java.util.*;

public class Main {

	// 입력고정
	static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
	static StringTokenizer tokens;
	// 세팅
	static ArrayList<Integer> operandList;
	static ArrayList<Character> operatorList;
	static int[] operandVisited;
	static int[] work;
	static int mini = Integer.MAX_VALUE;
	// 메소드
	
	//// 연산자 기준 순열 생성 => 연산 순서 생성 => 정상 작동 확인
	static void makePermu(int[] leaf, int nowDigit, final int targetDigit, final int pool, boolean[] visited) {
		// 바닥 조건
		if(nowDigit>=targetDigit) {
			// 추가 작업
			reset();
			// 전체 연산
			for (int i = 0; i < leaf.length; i++) {
				int operatorIndex = leaf[i];
				int maskingValue;
				if(operatorList.get(operatorIndex)=='+') {
					maskingValue = work[operatorIndex]+work[operatorIndex+1];
				} else {
					maskingValue = work[operatorIndex]-work[operatorIndex+1];
				}
				// 방문처리 + 값 마스킹 처리
				int left = operandVisited[operatorIndex];
				int right = operandVisited[operatorIndex+1];
				if(left==-1) {
					operandVisited[operatorIndex] = i;
					work[operatorIndex] = maskingValue;
				} else {
					DFS(operatorIndex, left, i, maskingValue);
				}
				
				if(right==-1) {
					operandVisited[operatorIndex+1] = i;
					work[operatorIndex+1] = maskingValue;
				} else {
					DFS(operatorIndex+1, right, i, maskingValue);
				}
			}
			// work의 모든 값이 연산 최종결과가 됨.
			mini = Math.min(mini, work[0]);
			return;
		}
		
		// 재귀 파트
		for(int i=0; i<pool;i++) {
			if(visited[i]) // 사용한 인덱스면 점프
				continue;
			visited[i] = true;
			leaf[nowDigit] = i;
			makePermu(leaf, nowDigit+1, targetDigit, pool, visited);
			visited[i] = false;
		}
	}
	
	//// 연산결과 마스킹 용도
	static void DFS(int x, final int compare, final int maskingIndex ,final int maskingValue) {  // 둘중의 최소값 골라서. 
		// 범위 초과시 버림 ==> DFS 타기 전에 해줄수도 있음. 동작 잘 안되면 여기부터 조지기.
		if(x<0 || x>operandList.size()-1)
			return;
		// 바닥 조건
		if(operandVisited[x]!=compare) // 비교값(compare)이랑 같을때만 확장. 비교값이랑 달라지면 확장불가!
			return;
		// 방문 처리가 아닌 마스킹
		operandVisited[x] = maskingIndex;
		work[x] = maskingValue;
		
		// 재귀 파트
		DFS(x-1, compare, maskingIndex, maskingValue);
		DFS(x+1, compare, maskingIndex, maskingValue);
	}
	
	//// 연산을 위한 재료 세팅
	static void reset() {
		Arrays.fill(operandVisited, -1);
		for (int i = 0; i < operandList.size(); i++) {
			work[i] = operandList.get(i);
		}
	}
	
	// 메인
	public static void main(String[] args) throws Exception {
		// 입력
		operandList = new ArrayList<>();
		operatorList = new ArrayList<>();
		
		tokens = new StringTokenizer(input.readLine(),"-+",true);
		for (int i = 0; ; i++) { // 무한루프
			if(tokens.hasMoreTokens()==false) { // 더 이상 토큰이 없으면 탈출
				break;
			}
			if(i%2==0) { // 짝수번째는 피연산자임. origin 리스트에 분류하기.
				int operand = Integer.parseInt(tokens.nextToken());
				operandList.add(operand);
			} else { // 홀수번쨰는 연산자임. operator 리스트에 분류하기.
				char operator = tokens.nextToken().charAt(0);
				operatorList.add(operator);
			}
		}
		// 세팅
		operandVisited = new int [operandList.size()];
		work = new int[operandList.size()];
		// 작업
		makePermu(new int[operatorList.size()], 0, operatorList.size(), operatorList.size(), new boolean[operatorList.size()]);
		// 출력
		System.out.println(mini);
	}

}

어떻게 풀까? - 수학

포인트

더하거나 빼기만 하는 식에서 최소값을 구하려면?
빼기 뒤에 있는 피 연산자를 최대한 크게 만들면 된다.
그러기 위해서는 빼기 뒤의 더하기를 먼저 계산해두면 된다.
빼기가 나올때까지는 수를 더해 나간다.
그리고 빼기가 나오면 그때부터 다시 새롭게 수를 더해 나간다.
그러면 값이 [양수, 음수, 음수, ... ,음수] 로 구성된다.
이 순서대로 계산해주면 전체식의 최소값이 나온다.

입력이 조금 까다로운 문제였는데 StringTokenizer에서 구분자 단위로 끊고 구분자도 포함시키는 메소드가 있어서 손쉽게 파싱했다.
✨ 레퍼런스: https://reakwon.tistory.com/90

코드

import java.io.*;
import java.util.*;

public class Main {

	// 입력고정
	static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
	static StringTokenizer tokens;
	// 세팅
	static ArrayList<Integer> operandList;
	static ArrayList<Character> operatorList;
	static ArrayList<Integer> subSums;
	// 메소드
	

	
	// 메인
	public static void main(String[] args) throws Exception {
		// 입력
		operandList = new ArrayList<>();
		operatorList = new ArrayList<>();
		subSums = new ArrayList<>();
		
		tokens = new StringTokenizer(input.readLine(),"-+",true);
		for (int i = 0; ; i++) { // 무한루프
			if(tokens.hasMoreTokens()==false) { // 더 이상 토큰이 없으면 탈출
				break;
			}
			if(i%2==0) { // 짝수번째는 피연산자임. origin 리스트에 분류하기.
				int operand = Integer.parseInt(tokens.nextToken());
				operandList.add(operand);
			} else { // 홀수번쨰는 연산자임. operator 리스트에 분류하기.
				char operator = tokens.nextToken().charAt(0);
				operatorList.add(operator);
			}
		}
		// 세팅

		// 작업
		int sum =0;
		sum += operandList.get(0); 	// 첫번째꺼는 미리 더해놓기 그래야 더하는 로직이 단순해짐. 지금 시점 하나만 더하면 되니까. 
									// 안 그러면 반복문에서 처음에 두개 더해야되는데 뒤에서도 같은 로직 쓰면서 계속 1번씩 중복해서 더해짐.
		for (int i = 0; i < operatorList.size(); i++) {
			if(operatorList.get(i) == '-') { // 연산자가 -가 나오기 전까지는 계속 더한다. -가 나오면 지금까지 더해놓은거 subSums에 저장하기. 
				subSums.add(sum); 	// -가 나오면 지금까지 더해놓은거 저장하기. 
				sum = 0;			// 다시 처음부터 더하기 위해서 초기화하기.
			}
			sum += operandList.get(i+1); 
		}
		// 마지막 한덩어리도 add
		subSums.add(sum);
		
		// 값 계산. 첫번째만 양수고 나머지는 다 음수이므로 빼줌.
		int answer = subSums.get(0);
		for (int i = 0+1; i < subSums.size(); i++) {
			answer -= subSums.get(i);
		}
		// 출력
		System.out.println(answer);
	}
}

퍼포먼스

[ 11,588 KB | 64 ms ]

마무리

퍼뮤테이션을 오랜만에 써서 시간복잡도가 끔찍하게 크다는 사실을 간과했다...
구현하는거 힘들었다...
StringTokenizer를 더 잘 쓸수 있게 되어 좋았다.