
문제 바로가기
https://www.acmicpc.net/problem/1753
문제 소개 및 재정의
심층분석
이전에 오버플로우가 발생했던 진짜이유 = 인접행렬
인접행렬의 ROW(Ingeger.MAX_VALUE 값이 포함돼있음)를 순회하면서 탐색을 했기 때문에 최소길이를 비교하고 갱신하는 로직에서 오버플로우가 발생했고 오버플로우 된 값이 최단거리 배열에 저장되면서 오버플로우된 값의 노드를 선택하고 전체적인 로직이 어그러졌기 때문이다.
if(visit[nextNode] == false) { // 방문이면 이미 최소화 루트를 통해서 결정된 값이기때문에 최소값임. 굳이 갱신할필요가 없음. 갱신하는 로직에 포함시켜도 됨. 어차피 더 작은 값이 안 붙어서 갱신안됨.
if(distance[currentNode] + nextWeight < distance[nextNode]) {
distance[nextNode] = distance[currentNode] + nextWeight;
}
}나이스한 다익스트라 - minHeap
망한 코드
import java.io.*;
import java.util.*;
public class BOJ_G4_1753_최단경로3 {
// 입력고정
static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer tokens;
static StringBuilder output = new StringBuilder();
static int V;
static int E;
// 세팅
static boolean[] visit;
static int[] distance;
// static ArrayList<int[]>[] graph; // int[]을 담는 ArrayList의 배열 ㅋㅋ..
static ArrayList<ArrayList<Node>> graph; // int[]을 담는 ArrayList의 배열 ㅋㅋ..
static int INF = 10*200_000+1;
// Node 클래스 // 노드 보다는 의미적으로 from이 주어졌을때 to로 가는 간선에 대한 정보와 가까움,
static class Node implements Comparable<Node>{
int num, weight;
Node(int num, int weight){
this.num = num;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}
// 메소드
//// 다익스트라
static void dijkstra(int start) {
// 부품 초기화 1
//// 방문배열 초기화 + init
visit = new boolean [V];
visit[start-1] = true;
//// 거리배열 초기화 + init
distance = new int [V];
Arrays.fill(distance, INF);
for (int i = 0; i < graph.get(start).size(); i++) {
Node node = graph.get(start).get(i);
distance[node.num] = node.weight;
}
distance[start-1] = 0;
// 부품 초기화 2
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.offer(new Node(start,0));
// 순회 시작
while(pq.isEmpty() ==false) {
Node nowNode = pq.poll();
if (visit[nowNode.num]) // 뽑은 노드가 방문한 노드라면 무시
continue;
visit[nowNode.num] = true;
for (int next = 0; next < graph.get(nowNode.num).size(); next++) {
Node nextNode = graph.get(nowNode.num).get(next);
if(visit[nextNode.num]) // 방문이면 이미 최소화 루트를 통해서 결정된 값이기때문에 최소값임. 굳이 갱신할필요가 없음.
continue;
if(distance[nowNode.num] + nextNode.weight < distance[nextNode.num]) {
distance[nextNode.num] = distance[nowNode.num] + nextNode.weight;
pq.add(nextNode);
}
}
}
}
// 메인
public static void main(String[] args) throws NumberFormatException, IOException {
// 입력
tokens = new StringTokenizer(input.readLine());
V = Integer.parseInt(tokens.nextToken());
E = Integer.parseInt(tokens.nextToken());
int start = Integer.parseInt(input.readLine());
graph = new ArrayList();
for (int i = 0; i < V; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < E; i++) {
tokens = new StringTokenizer(input.readLine());
int from = Integer.parseInt(tokens.nextToken())-1; // -1 해서 그래프에 맞게 넣음.
int to = Integer.parseInt(tokens.nextToken())-1; // -1
int weight = Integer.parseInt(tokens.nextToken());
// 인접리스트 생성 + 업데이트
boolean isAlready = false;
for (int j = 0; j < graph.get(from).size(); j++) {
int alreadyNode = graph.get(from).get(j).num;
int alreadyWeight = graph.get(from).get(j).weight;
if(alreadyNode==to) { // 같은 노드를 잇는 간선이 기존에 있음 => 최소값만 남김.
graph.get(from).get(j).weight = Math.min(weight, alreadyWeight);
isAlready = true;
break;
}
}
if(isAlready==false) { // 기존에 없다고? 추가해~
graph.get(from).add(new Node(to, weight));
}
// 인접리스트 생성만
// graph.get(from).add(new Node(to, weight));
}
// 세팅
// 작업
dijkstra(start);
// 출력
for (int i = 0; i < V; i++) {
if(distance[i]==INF) {
output.append("INF").append("\n");
} else {
output.append(distance[i]).append("\n");
}
}
System.out.println(output);
}
}시행착오 복기
이전 코드를 수정하는 방식으로 짰더니 오류가 많이 발생했다.
수정 1: 이전 코드에서는
start를 인덱스번호가 아니고 Node번호로 받아와서 코드 안에서start-1처리를 해줘야했다.
번거로움을 덜기 위해서start입력을 받을때 -1처리를 해줬다.
실수 1: 방문 배열 초기화
큐에 처음 노드를 넣을때, 이전 코드에서는 첫 노드에 대해서 미리 방문처리를 했었다.
visit[start-1] = true;
이미 방문한 노드는 작업처리 없이 건너뛰기 때문에 미리 초기화한 초항이 아무 작업도 하지 않으니 디큐를 딱 한번만 하는 불상사가 발생했다.
그리고 우선순위 큐를 쓸때는 큐에서 꺼냈을 때 방문처리를 해줘야한다.
실수 2: 거리 배열 초기화
큐에 처음 노드를 넣을때, 이전 코드에서는 첫노드가 갈수있는 노드에 대한 최소거리를 미리 갱신했었다.
for (int i = 0; i < graph.get(start).size(); i++) {
Node node = graph.get(start).get(i);
distance[node.num] = node.weight;
}
아래 while문에서 Node를 꺼내고 난후 업데이트 가능여부를 판단할때, 미리 업데이트를 해놨기 때문에 업데이트 불가능 판정이 뜬다.
그리고 업데이트가 가능할때 경로가 확장된다.
따라서 다음 노드로 확정이 불가능한 코드였다.
실수 3: 큐에 넣는 Node와 graph에서 꺼내는 Node를 혼동했다.
nextNode는 nowNode에서 다른 노드로 갈수있는 간선에 대한 정보이다.
따라서 다음노드의 번호와 그때까지의 최소거리를 Node에 담아서 보내줘야 했다.
정상 코드
package lecture.d0902;
import java.io.*;
import java.util.*;
public class BOJ_G4_1753_최단경로3 {
// 입력고정
static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer tokens;
static StringBuilder output = new StringBuilder();
static int V;
static int E;
// 세팅
static boolean[] visit;
static int[] distance;
static ArrayList<ArrayList<Node>> graph; // int[]을 담는 ArrayList의 배열 ㅋㅋ..
static int INF = 10*200_000+1;
// Node 클래스 // 노드 보다는 의미적으로 from이 주어졌을때 to로 가는 간선에 대한 정보와 가까움,
static class Node implements Comparable<Node>{
int num, weight;
Node(int num, int weight){
this.num = num;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}
// 메소드
//// 다익스트라
static void dijkstra(int start) {
// 조기 종료 조건
int visitedCount = 0;
// 부품 초기화 1
//// 방문배열 초기화 + init
visit = new boolean [V];
//// 거리배열 초기화 + init
distance = new int [V];
Arrays.fill(distance, INF);
distance[start] = 0;
// 부품 초기화 2
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.offer(new Node(start,0));
// 순회 시작
while(pq.isEmpty() ==false) {
// 조기 종료
if(visitedCount==V)
break;
Node nowNode = pq.poll();
if (visit[nowNode.num]) // 뽑은 노드가 방문한 노드라면 무시
continue;
// 방문처리
visit[nowNode.num] = true;
visitedCount++;
// 최단거리 갱신 + 인큐
for (int next = 0; next < graph.get(nowNode.num).size(); next++) {
Node nextNode = graph.get(nowNode.num).get(next);
if(visit[nextNode.num]) // 방문이면 이미 최소화 루트를 통해서 결정된 값이기때문에 최소값임. 굳이 갱신할필요가 없음.
continue;
if(distance[nowNode.num] + nextNode.weight < distance[nextNode.num]) {
distance[nextNode.num] = distance[nowNode.num] + nextNode.weight;
pq.add(new Node(nextNode.num, distance[nextNode.num]));
}
}
}
}
// 메인
public static void main(String[] args) throws NumberFormatException, IOException {
// 입력
tokens = new StringTokenizer(input.readLine());
V = Integer.parseInt(tokens.nextToken());
E = Integer.parseInt(tokens.nextToken());
int start = Integer.parseInt(input.readLine())-1;
graph = new ArrayList();
for (int i = 0; i < V; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < E; i++) {
tokens = new StringTokenizer(input.readLine());
int from = Integer.parseInt(tokens.nextToken())-1; // -1 해서 그래프에 맞게 넣음.
int to = Integer.parseInt(tokens.nextToken())-1; // -1
int weight = Integer.parseInt(tokens.nextToken());
// 인접리스트 생성 + 업데이트
// boolean isAlready = false;
// for (int j = 0; j < graph.get(from).size(); j++) {
// int alreadyNode = graph.get(from).get(j).num;
// int alreadyWeight = graph.get(from).get(j).weight;
// if(alreadyNode==to) { // 같은 노드를 잇는 간선이 기존에 있음 => 최소값만 남김.
// graph.get(from).get(j).weight = Math.min(weight, alreadyWeight);
// isAlready = true;
// break;
// }
// }
// if(isAlready==false) { // 기존에 없다고? 추가해~
// graph.get(from).add(new Node(to, weight));
// }
// 인접리스트 생성만
graph.get(from).add(new Node(to, weight));
}
// 세팅
// 작업
dijkstra(start);
// 출력
for (int i = 0; i < V; i++) {
if(distance[i]==INF) {
output.append("INF").append("\n");
} else {
output.append(distance[i]).append("\n");
}
}
System.out.println(output);
}
}퍼포먼스 비교
모든 간선을 인접리스트에 저장했을때 [
115_948 KB|612 ms]
가중치가 최소값인 간선만 저장했을때 [
112_780 KB|2_268 ms]
의외로 Heap을 사용할때는 나이브하게 모든 간선을 인접리스트에 넣어야 빠르다.
간선의 개수가 많고 그만큼 중복된 간선의 개수가 많기 때문에 그런것으로 추정된다.
모든 노드를 방문했을때 큐에 남아있는 노드를 다 안 빼고 조기종료시 [
115_676 KB|624 ms]
큐가 빌때까지 반복문이 실행되므로 모든 노드 방문 후 남아있는 노드를 빼기 위해서 돌아가는 부분을 생략했을때 오히려 더 오래 걸렸다.
불필요한 최적화로 생각된다.
이해를 돕기 위한 다익스트라 시뮬레이션
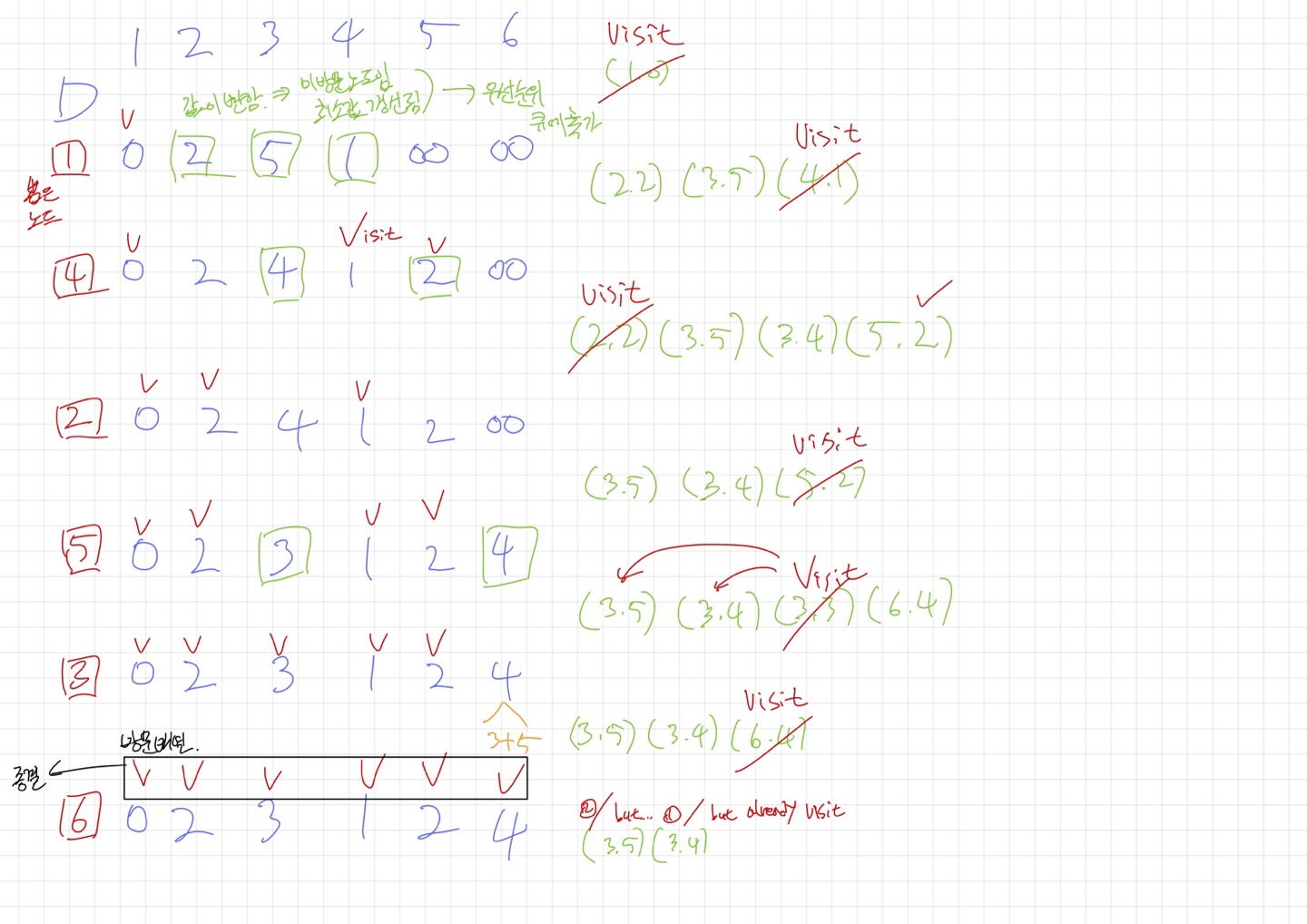
군더더기 제거한 코드
import java.io.*;
import java.util.*;
public class BOJ_G4_1753_최단경로3 {
// 입력고정
static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer tokens;
static StringBuilder output = new StringBuilder();
static int V;
static int E;
// 세팅
static boolean[] visit;
static int[] distance;
static ArrayList<ArrayList<Node>> graph; // int[]을 담는 ArrayList의 배열 ㅋㅋ..
static int INF = 10*200_000+1;
// Node 클래스 // 노드 보다는 의미적으로 from이 주어졌을때 to로 가는 간선에 대한 정보와 가까움,
static class Node implements Comparable<Node>{
int num, weight;
Node(int num, int weight){
this.num = num;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}
// 메소드
//// 다익스트라
static void dijkstra(int start) {
// 부품 초기화 1
//// 방문배열 초기화
visit = new boolean [V];
//// 거리배열 초기화 + init
distance = new int [V];
Arrays.fill(distance, INF);
distance[start] = 0;
// 부품 초기화 2
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.offer(new Node(start,0));
// 순회 시작
while(pq.isEmpty() ==false) {
Node nowNode = pq.poll();
if (visit[nowNode.num]) // 뽑은 노드가 방문한 노드라면 무시
continue;
visit[nowNode.num] = true;
for (int next = 0; next < graph.get(nowNode.num).size(); next++) {
Node nextNode = graph.get(nowNode.num).get(next);
if(visit[nextNode.num]) // 방문이면 이미 최소화 루트를 통해서 결정된 값이기때문에 최소값임. 굳이 갱신할필요가 없음.
continue;
if(distance[nowNode.num] + nextNode.weight < distance[nextNode.num]) {
distance[nextNode.num] = distance[nowNode.num] + nextNode.weight;
pq.add(new Node(nextNode.num, distance[nextNode.num]));
}
}
}
}
// 메인
public static void main(String[] args) throws NumberFormatException, IOException {
// 입력
tokens = new StringTokenizer(input.readLine());
V = Integer.parseInt(tokens.nextToken());
E = Integer.parseInt(tokens.nextToken());
int start = Integer.parseInt(input.readLine())-1;
graph = new ArrayList();
for (int i = 0; i < V; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < E; i++) {
tokens = new StringTokenizer(input.readLine());
int from = Integer.parseInt(tokens.nextToken())-1; // -1 해서 그래프에 맞게 넣음.
int to = Integer.parseInt(tokens.nextToken())-1; // -1
int weight = Integer.parseInt(tokens.nextToken());
// 인접리스트 생성
graph.get(from).add(new Node(to, weight));
}
// 세팅
// 작업
dijkstra(start);
// 출력
for (int i = 0; i < V; i++) {
if(distance[i]==INF) {
output.append("INF").append("\n");
} else {
output.append(distance[i]).append("\n");
}
}
System.out.println(output);
}
}
