문제 바로가기

https://www.acmicpc.net/problem/2343

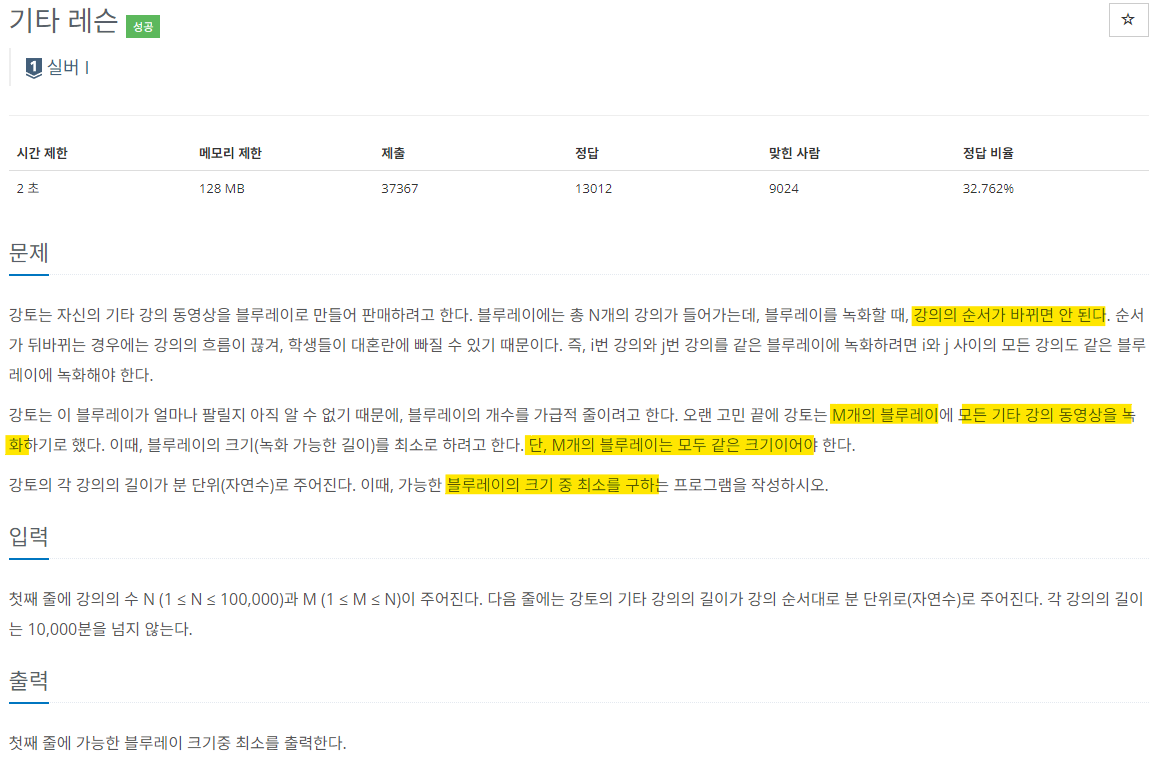
문제 소개

문제를 이해하기 편하게 재정의

고정된 순서의 요소들(강의의 순서가 바뀌면 안된다 = 정렬상태 )을 박스에 모두 담아야 한다.
박스의 개수는 고정돼있고.
모든 박스의 크기는 동일하다.
이때 박스의 크기를 최소화하시오.

이 문제에서 박스 == 블루레이.

어떻게 풀까? - 이진탐색

범위 정의

위에서 문제를 재정의 하는 과정에서 느꼈지만, 상술한 문제는 이진탐색 문제의 패턴중 하나이다.
문제의 조건에 부합하는 박스의 크기(Size)는 여러개 있을수 있다.
그중에서 최소값을 구해야하는 문제다.

먼저 문제의 조건에 부합하는 Size의 범위에 대해 고민해봐야한다.
진짜로 필요한 범위를 A라고 하자.
A를 포함하는 범위인 B안에서 Naive하게 이진탐색을 해도 Size를 구할수 있다.
=> 넉넉하게 잡자. 혹시 모르니까.
해당 범위 안에 찾고 싶은 값이 있으면 찾을수 있다가 포인트다.

그렇게 범위 B를 잡아보면 아래와 같다.
0<=Size<= total(모든 강의들 크기의 합)

Size가 0이면 아무것도 못 담겠지만.
일단 크기와 관련된 것이므로 음수는 제외하고 범위를 0부터 시작해도 될것으로 보인다.

Size가 total일때는 하나의 박스에 모든 강의를 담을수 있다.
이 이상 커지는 것은 의미가 없다.

범위 축소

이진 탐색은 탐색할 범위를 절반씩 줄여나가는 방식의 탐색이다.
따라서 시간복잡도는 O(logN)이다.
10억개의 배열중 원하는 값을 찾는데 30번의 연산이면 충분한것이다.

대신 탐색대상이 정렬된 상태여야 한다는 조건이 있다.
탐색대상이 정렬돼 있어야 중앙값을 확인한 후에 범위를 축소할때 어느 방향으로 축소할건지 결정할수 있기 때문이다.
중앙값이 우리가 원하는 값보다 크면 더 작은 쪽으로 범위를 축소하고
중앙값이 우리가 원하는 값보다 작으면 더 큰 쪽으로 범위를 축소한다.

활용

많이 풀어본건 아니지만 지금까지 본 이진탐색의 문제는
이진 탐색 로직과 그 안에서 범위축소 방향을 결정해주는 로직으로 구성된다.

이 문제에서는 블루레이의 크기를 구해야 한다.
이진 탐색 로직으로 크기를 하나 정한 후.
해당 크기를 단위로 하는 블루레이로 모든 강의를 담을수 있다면,
블루레이의 크기를 줄여서 시도해봐야한다.
모든 강의를 담을수 없다면, 크기를 늘려서 시도해봐야 한다.
정반합과 같이 크기를 늘리고 줄이고를 반복하다보면 최적화된 값에 도달하게 되는 것이다.

이진탐색 포인트

바닥 조건: 시작점의 값이 끝점의 값보다 클때 탈출.
범위 : [시작, 중앙-1] | [중앙+1, 끝]
길이가 작은 리스트에 대해서 직접 시뮬레이션 하면 위 구조를 이해할수 있다.

코드

package study.week7;

import java.io.*;
import java.util.*;

public class BOJ_2343_기타_레슨 {
	
	// 입력 고정
	static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
	static StringTokenizer tokens;
	
	// 세팅
	static int N;
	static int M;
	static int[] lectureList;

	static int minK; // 블루레이의 길이! == 이진탐색으로 값을 찾을 대상
	
	// 용량 적당한가?
	static boolean sizeEnough(int k) {
		int quatity = M-1; 	// 아 시작할때 블루레이를 하나 꺼내서 담아야하구나!
		int sum = 0;		// 블루레이 사용 용량 초기화
		for (int i = 0; i < lectureList.length; i++) {
			// 블루레이 용량에 들어가지면 넣고, 안되면 블루레이를 새로 꺼내서 담는다.
			// 그런데 여기서 문제가 발생한다... 블루레이 용량보다 큰값이면 블루레이에 못 담는데 여기서는 else문에서 담고 넘겨버리는게 문제다.
			// 따라서 그런 경우 false를 뱉고 탈출을 해야한다.
			if(lectureList[i]>k) {
				return false;
			}
			
			if(sum+lectureList[i]<=k) {
				sum += lectureList[i];
			} else {
				quatity --;
				sum =0;
				sum += lectureList[i];
			}
		}
		if(quatity>=0) {
			return true;
		} else {
			return false;
		}
	}
	
	// 재귀적 이진탐색
	static void binarySearch(int start, int end) {
		// 바닥 조건
		if(start > end) {
			return;
		}
		
		// 재귀파트
		int mid = (start+end)/2;
		boolean isOK = sizeEnough(mid);
		if(isOK) {
			minK = mid;
			binarySearch(start, mid-1);
		} else {
			binarySearch(mid+1, end);
		}
	}
	
	
	
	public static void main(String[] args) throws IOException {
		// 입력부
		tokens = new StringTokenizer(input.readLine());
		N = Integer.parseInt(tokens.nextToken());
		M = Integer.parseInt(tokens.nextToken());
		lectureList = new int[N];
		tokens = new StringTokenizer(input.readLine());
		for (int i = 0; i < N; i++) {
			lectureList[i] = Integer.parseInt(tokens.nextToken());
		}
		
		// 세팅부
		int sum =0;
		for (int i = 0; i < lectureList.length; i++) {
			sum+=lectureList[i];
		}
		
		// 작업부
//		binarySearch(1, (int) Math.pow(10, 9));
		binarySearch(0, sum+1);
		
		// 출력부
		System.out.println(minK);
		
	} // 메인 종료

}

퍼포먼스

["22,388"KB | "216" ms]