문제 바로가기

https://www.acmicpc.net/problem/3079

문제 소개 및 재정의

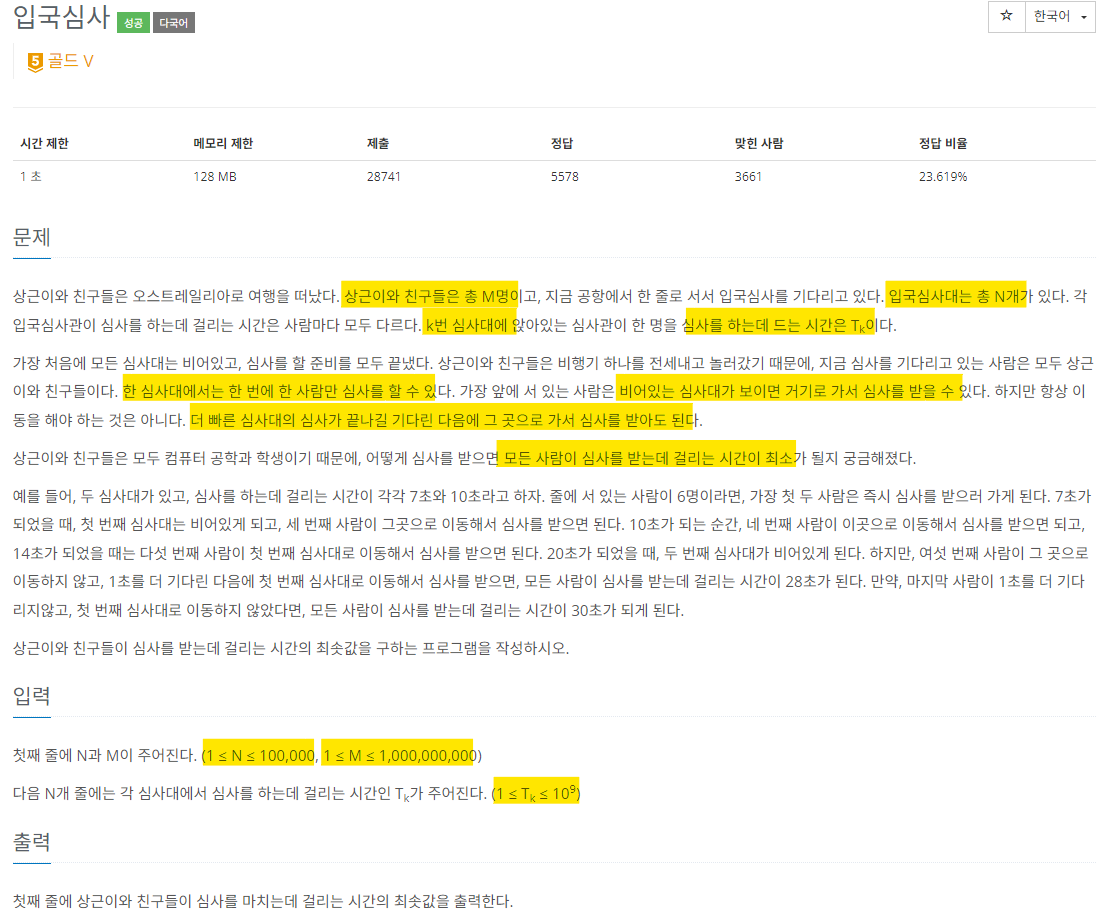
M명의 사람이 N개의 창구에서 심사를 받는데 걸리는 최소 시간을 구하시오.
각각의 창구는 심사하는데 걸리는 시간이 다를수 있음.

문제 패턴

이전 이진탐색 포스트에서 정제한 패턴에 비춰보면.
M개의 아이템 N개의 박스로 보여지기도 한다.
박스의 크기는 전체시간으로 결정된다.
그리고 입력의 크기가 심각하게 크다. 10억!
이진탐색으로 해결해야겠다는 생각이 먼저 들었다.

어떻게 풀까? - 시뮬레이션

시도에 대한 배경

그런데 빈 곳으로 바로 가지 않고, 끝나는 시간이 더 빠른 곳이 빌때까지 기다린다는 문제의 조건을 보고 이 점을 보장하는 방법을 생각하게 됐다.
다시 말하면, 심사를 했을떄 끝나는 시간이 더 빠른 곳에 간다는 것이다.

대기열 + 제일 먼저 끝나는 곳으로 간다는 점에서 우선순위 큐 그 자체라는 생각이 든다.

포인트

모든 입국 심사대를 우선순위 큐에 인큐한다.
입국 심사대는 심사를 한번 하는데 필요한 시간(loading) 과 지금 하고 있는 심사가 끝나는 시간(endTime)을 가진다.
endTime에 대해서 정렬을 해두면 디큐할때마다 가장 빨리 끝나는 창구가 나오게 된다.

따라서 디큐가 가지는 의미는 한명이 심사를 끝냈다는 것과 그 창구에서 심사가 가능하다는 의미를 가진다.
따라서 디큐할때 심사를 한 사람의 수(peopleCount)를 세주고, 다시 해당 창구에서 심사를 시작하도록 endTime에 loading을 더해줘서 인큐한다.

이렇게하면 끝나는 시간이 빠른 순으로 입국심사대를 사용하게 된다.
따라서, 더 빠른 곳이 빌때까지 기다렸다 사용하는 것이 보장된다.

인큐와 디큐가 무한히 반복되는 구조이므로 peopleCount==M일때 탈출한다.

코드 - 우선순위 큐에 클래스를 인큐

import java.io.*;
import java.util.*;

public class BOJ_3079_입국심사 {
	// 입력 고정
	static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
	static StringTokenizer tokens;
	// 세팅
	static int N;
	static int M;
	// 메소드
	
	// 클래스
	static class Simsa implements Comparable<Simsa> {
		int loading;
		int endTime;
		
		Simsa(int loading, int endTime){
			this.loading = loading;
			this.endTime = endTime;
		}
		
		@Override
		public int compareTo(Simsa o) {
			return Integer.compare(this.endTime, o.endTime);
		}
	}
	
	// 메인
	public static void main(String[] args) throws Exception {
		
		// 입력
		tokens = new StringTokenizer(input.readLine());
		N = Integer.parseInt(tokens.nextToken());
		M = Integer.parseInt(tokens.nextToken());
		
		PriorityQueue<Simsa> pq = new PriorityQueue<Simsa>();
		for(int i=0; i<N; i++) {
			int loading = Integer.parseInt(input.readLine());
			pq.offer(new Simsa(loading, loading));
		}
		// 세팅
		// 작업
		int peopleCount = 0;
		// 디큐할때마다 한명의 심사가 끝남. M명의 심사가 끝났을때 카운트는 M임. 디큐하고나서 카운트가 M이라면 해당 Simsa의 endTime을 값으로 제출.
		while(pq.isEmpty()==false) {
			Simsa nowEndSimsa = pq.poll(); 
			peopleCount++;
			int loading = nowEndSimsa.loading;
			int endTime = nowEndSimsa.endTime;
			pq.offer(new Simsa(loading, endTime+loading));
			if(peopleCount==M) {
				System.out.println(endTime);
				break;
			}
		}
		// 출력
	}
}

코드 - 우선순위 큐에 int[]를 인큐

import java.io.*;
import java.util.*;

public class BOJ_3079_입국심사2 {
	// 입력 고정
	static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
	static StringTokenizer tokens;
	// 세팅
	static int N;
	static int M;
	static int[] origin;
	// 메소드
	
	// 클래스
	static class Simsa implements Comparable<Simsa> {
		int loading;
		int endTime;
		
		Simsa(int loading, int endTime){
			this.loading = loading;
			this.endTime = endTime;
		}
		
		@Override
		public int compareTo(Simsa o) {
			return Integer.compare(this.endTime, o.endTime);
		}
	}
	
	// 메인
	public static void main(String[] args) throws Exception {
		
		// 입력
		tokens = new StringTokenizer(input.readLine());
		N = Integer.parseInt(tokens.nextToken());
		M = Integer.parseInt(tokens.nextToken());
		
		origin = new int[N];
		PriorityQueue<int[]> pq = new PriorityQueue<int[]>(
			Comparator.comparingInt(o->o[1])
		);
		
		for(int i=0; i<N; i++) {
			int loading = Integer.parseInt(input.readLine());
			pq.offer(new int[] {loading,loading});
		}
		// 세팅
		// 작업
		int peopleCount = 0;
		// 디큐할때마다 한명의 심사가 끝남. M명의 심사가 끝났을때 카운트는 M임. 디큐하고나서 카운트가 M이라면 해당 Simsa의 endTime을 값으로 제출.
		while(pq.isEmpty()==false) {
			int[] nowEndSimsa = pq.poll(); 
			peopleCount++;
			int loading = nowEndSimsa[0];
			int endTime = nowEndSimsa[1];
			pq.offer(new int[] {loading, endTime+loading});
			if(peopleCount==M) {
				System.out.println(endTime);
				break;
			}
		}
		// 출력
	}
}

한계

아니나 다를까 잘 안됐다!
이진 탐색 문제인데 그렇게 안 풀었으니까.
하지만 우선순위 큐에 미숙했던터라 우선순위 큐를 연습한 것에 만족했다.

공간 복잡도
사람수인 M의 크기가 O(10억)이기 때문에 10억개의 클래스를 만들어야 한다.
Integer 두개로 구성된 클래스이기 때문에 단순하게 계산해봐도 다음과 같다.
8byte10억2 = 160억 byte => 대략 16GB의 메모리를 필요로 한다

시간 복잡도
디큐를 10억번 해야한다.
인큐는 10억번(디큐할때마다 인큐) + 10만번(우선순위 큐 초기화) 해야한다.
(초기화 이후 디큐할때마다 인큐하므로)
따라서 대략 20억번의 우선순위 큐 업데이트가 발생한다.
우선순위 큐의 사이즈는 0부터 시작해서 10만에서 고정된다.
우선순위 큐를 1번 업데이트 하는데는 log2(10만) => 대략 16번의 연산이 필요하다.
따라서 20억*16==320억번의 연산이 필요하다.
연산량이 많다는 것은 그만큼 많은 정보를 가질수 있다는 뜻이다.
O(M*log(N))

어떻게 풀까? - 이진 탐색

포인트

이진 탐색할 범위를 먼저 구해야한다.
0~아무 심사 시간*M
전체 시간은 양수이므로 범위는 0부터 시작한다.
어떤 창구라도 M번 심사하면 되므로 아무 심사 시간*M 까지다.

최악의 경우 모든 심사대의 심사시간이 10억(=10^9)이다.
그리고 심사 받아야하는 사람의 수도 10억이다.
이 경우 전체 시간은 10^18이다.
10^3은 대략적으로 2^10이므로 10^18은 2^60이 된다.
따라서 전체 시간과 관련된 변수를 int타입으로 저장하면 오버플로우가 발생한다.
그래서 long타입으로 저장돼야 한다.
long타입도 2^63-1의 자연수까지만 표현가능해서 제법 꽉 찬다.

탐색 범위의 중앙값인 mid 시간내에 M명의 입국심사가 가능한지 확인한다.
가능하다면 시간을 줄여보기 위해서 탐색범위를 시작~중앙값-1로 결정한다.
(성공했을때 성공한 값인 mid를 저장해둠으로써 최적값을 관리한다.)
불가능하다면 시간을 늘려봐야 하므로 탐색범위를 중앙값+1~끝 으로 결정한다.

코드 - 이진 탐색

static void bs(long start, long end) {
	// 바닥 조건
	if(start>end)
		return;
	
	// 재귀 파트
	long mid = (start+end)/2;
	if(isOK(mid)) {
		best = mid; // 성공할때마다 저장. 가장 최신 성공의 값으로 갱신됨. 최소값 유지.
		bs(start, mid-1);
	}else {
		bs(mid+1,end);
	}
}

코드 - 탐색 방향 결정 로직

static boolean isOK(long mid) {
	long sum =0;
	for(int i=0; i<N; i++) {
		sum += mid/origin[i]; // 정해진 시간(mid)동안 각각의 입국심사대가 처리할수 있는 사람의 수. 그것들의 합. // mid/origin[i]이 맞는데... origin[i]/mid 이따구로 해놨음.
	}
	if(sum>=M) // mid 시간동안 M명 이상을 처리할수 있음. ==> mid를 줄여보자
		return true;
	else // sum<M ==> mid 시간동안 M명을 처리할 수 없음. ==> mid를 늘려보자
		return false;
}

한계

논리적으로 완벽한데 자꾸 답이 안 나와서 힘들었다.
범위를 심사시간 최대값*M으로 하면 채점이 더 되고.
origin을 정렬해두면 채점이 더 되고.
논리적으로 결론의 방향이 일정하지 않아서 아주 많이 헤맸다.
일단 논리적으로는 문제가 없다고 판단하여 다른 사람의 코드와 비교하면서 다른 점을 분석했다.

같은 자바를 사용한 풀이 코드도 나와 같은 타이밍에서 막혔다.
테스트 케이스가 추가된듯하다.
파이썬 풀이 코드와 비교해봤다.
완전히 똑같은 로직인데, 파이썬 코드는 통과했다.
자바혐오를 멈춰주세요 ㅠ
자바와 파이썬의 다른점이 키포인트일것으로만 추정된다.

해당 문제의 질문게시판에서 나와 같은 증상을 호소하는 사람을 봤고 그곳에 정답이 있었다. https://www.acmicpc.net/board/view/141496

심사가 끝난 사람을 구하는 과정에서 이미 M을 넘겼으면 더 이상 더하지 않고 끝내야 안전하다.
최악의 경우를 가정해보자.
하나의 심사대가 10억의 시간을 소모하고 나머지는 1을 소모한다.
심사를 받아야 하는 사람의 수는 10억명이다.
탐색범위는 (0~10^18)가 된다.
처음에 들어오는 mid의 값은 (10^18)/2다.
심사가 끝난 사람 수인 mid/각 심사대 소요시간을 더하게되면
(10^18)/2를 (10억-1)번 더하게 된다.
그 값이 (10^27)/2 ==> 2^(90-1)에 육박한다.
따라서 long에서도 오버플로우가 발생한다.

그것을 막기 위해서 M을 넘겼을때 더 이상 더하지 않도록 반복문을 조기 종료하는 방법이 있다.
(M을 넘겼을때 우리가 필요한 정보는 이미 획득된 상태이므로)
한번에 최대로 더할수 있는 값은 (10^18)/2이다.
두번 더하더라도 (10^18)으로 오버플로우가 발생하지 않는 값이다.
M은 10^9가 최대이므로, M을 넘긴 상태에서 최대값이 들어오더라도 오버플로우는 발생하지 않는다.

코드 - 탐색 방향 결정 로직 (수정됨)

static boolean isOK(long mid) {
	long sum =0;
	for(int i=0; i<N; i++) {
		if(sum>=M) 
			break;
		sum += mid/origin[i]; // 정해진 시간(mid)동안 각각의 입국심사대가 처리할수 있는 사람의 수. 그것들의 합. // mid/origin[i]이 맞는데... origin[i]/mid 이따구로 해놨음.
	}
	if(sum>=M) // mid 시간동안 M명 이상을 처리할수 있음. ==> mid를 줄여보자
		return true;
	else // sum<M ==> mid 시간동안 M명을 처리할 수 없음. ==> mid를 늘려보자
		return false;
}

전체 코드

import java.io.*;
import java.util.*;

public class BOJ_3079_입국심사4 {
	// 입력 고정
	static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
	static StringTokenizer tokens;
	// 세팅
	static int N;
	static int M;
	static int[] origin;
	static long best;
	// 메소드
	//// 이진탐색
	static void bs(long start, long end) {
		// 바닥 조건
		if(start>end)
			return;
		
		// 재귀 파트
		long mid = (start+end)/2;
		if(isOK(mid)) {
			best = mid; // 성공할때마다 저장. 가장 최신 성공의 값으로 갱신됨. 최소값 유지.
			bs(start, mid-1);
		}else {
			bs(mid+1,end);
		}
	}
	
	//// 탐색 방향 결정 로직
	static boolean isOK(long mid) {
		long sum =0;
		for(int i=0; i<N; i++) {
			if(sum>=M) 
				break;
			sum += mid/origin[i]; // 정해진 시간(mid)동안 각각의 입국심사대가 처리할수 있는 사람의 수. 그것들의 합. // mid/origin[i]이 맞는데... origin[i]/mid 이따구로 해놨음.
		}
		if(sum>=M) // mid 시간동안 M명 이상을 처리할수 있음. ==> mid를 줄여보자
			return true;
		else // sum<M ==> mid 시간동안 M명을 처리할 수 없음. ==> mid를 늘려보자
			return false;
	}
	
	
	// 메인
	public static void main(String[] args) throws Exception {
		
		// 입력
		tokens = new StringTokenizer(input.readLine());
		N = Integer.parseInt(tokens.nextToken());
		M = Integer.parseInt(tokens.nextToken());
		
		origin = new int[N];
		for(int i=0; i<N; i++) {
			origin[i] = Integer.parseInt(input.readLine());
		}
		// 세팅
		// 작업
		bs((long) 0, (long) origin[0]*M); // 아무 입국심사대에서나 M번처리하면 모두 처리 가능하므로 끝값을 그렇게 설정.
		// 출력
		System.out.println(best);
	}
}

퍼포먼스

[ 22_508 KB | 252 ms ]

마무리

이 캐릭터는 수를 더할때 꼭 오버플로우를 생각하는 직업병이 추가되었습니다.