[백준]23040 : 누텔라 트리 (Easy)

비가츄·2024년 2월 23일

문제 설명

누텔라 트리 문제 링크는 아래에.
누텔라 트리 (Easy)

위의 누텔라 로고처럼 시작은 검정, 이후는 빨강 노드로 구성된 경로의 개수를 찾는 문제이다.
누텔라 경로의 조건은 아래와 같다.

$k$ 는 $2$ 이상이다.
각 $1 \le i \le k-1$ 에 대해, $v_i$ 와 $v_{i+1}$ 은 트리에서 간선으로 직접 연결되어 있다.
$v_1$ 은 검은색이다.
각 $2 \le i \le k$ 에 대해, $v_i$ 는 빨간색이다.

접근

union-find를 이용한 접근

단순하게 DFS로 접근하면 N이 100,000이라 시간초과가 날 것 같았다.
중복 연산을 줄이기 위해, 검정 노드와 연결된 각 빨강 노드의 길이를 먼저 연산해서 사용하자는 아이디어가 떠올랐다.

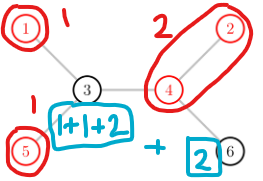
위의 그림과 같이 연결된 빨강 노드의 개수를 알면 검정 노드에서 자신과 직접 연결된 빨강 노드만을 확인해서 답을 구할 수 있다.
때문에 연결된 빨강 노드의 개수를 계산하기 위해 union find 알고리즘을 채택했다.

아래는 첫 번째로 시도한 코드이다.

# 누텔라 트리 (Easy) : 골드 3
import sys
input = sys.stdin.readline

N = int(input())
E = [[] for _ in range(N+1)] # 간선
P = [i for i in range(N+1)] # 집합 부모 정보
L = [0 for _ in range(N+1)] # 집합 크기(rank)
B = []  # 검정 노드
R = []  # 빨강 노드
answer = 0

# 유니온 파인드 사용
def union(a, b):
    a = find(a)
    b = find(b)
    if a==b:
        return
    if L[b] > L[a]:
        P[a] = b
    else:
        P[b] = a
        if L[b] == L[a]:
            L[a] += 1

def find(a):
    if a!=P[a]:
        P[a] = find(P[a])
    return P[a]


# 간선 정보 저장
for _ in range(N-1):
    u, v = map(int, input().split())
    E[u].append(v)
    E[v].append(u)


# 노드 색상별로 분리
C = " " + input()

for i in range(1, len(C)):
    if C[i] == "R":
        R.append(i)
        # 집합 크기(rank) 초기화
        L[i] = 1

    elif C[i] == "B":
        B.append(i)

# 빨강 노드에 대해 유니온파인드 실행
for n in R:
    for m in E[n]:
        if C[m]=="R":
            union(n, m)

# 검정 노드를 포함하는 모든 누텔라 찾기
for n in B:
    # 검정끼리는 L[m]이 0이므로 다 더함
    for m in E[n]:
        answer += L[find(m)]

print(answer)

해당 코드는 내자마자 틀렸습니다를 받았다..
아무리 생각해도 접근은 맞는 것 같은데 뭐가 문제인가 싶었다.

디버깅

알고보니 집합 크기로 쓰기 위해 사용한 L을 나도 모르게 습관적으로 rank로 쓰고 있었다!!
union find 최적화를 목적으로 사용한 배열이 아니기에 원래에 목적에 맞게 union 함수를 아래와 같이 수정했다.

def union(a, b):
    a = find(a)
    b = find(b)
    if a!=b:
        P[b] = a
        L[a] += L[b]

소스코드

최종적으로 제출한 코드는 다음과 같다.

# 누텔라 트리 (Easy) : 골드 3
import sys
sys.setrecursionlimit(100000)
input = sys.stdin.readline

N = int(input())
E = [[] for _ in range(N+1)] # 간선
P = [i for i in range(N+1)] # 집합 부모 정보
L = [0 for _ in range(N+1)] # 집합 크기(rank)
B = []  # 검정 노드
R = []  # 빨강 노드
answer = 0

# 유니온 파인드 사용
def union(a, b):
    a = find(a)
    b = find(b)
    if a!=b:
        P[b] = a
        L[a] += L[b]

def find(a):
    if a!=P[a]:
        P[a] = find(P[a])
    return P[a]


# 간선 정보 저장
for _ in range(N-1):
    u, v = map(int, input().split())
    E[u].append(v)
    E[v].append(u)


# 노드 색상별로 분리
C = " " + input()

for i in range(1, len(C)):
    if C[i] == "R":
        R.append(i)
        # 집합 크기(rank) 초기화
        L[i] = 1

    elif C[i] == "B":
        B.append(i)

# 빨강 노드에 대해 유니온파인드 실행
for n in R:
    for m in E[n]:
        if C[m]=="R":
            union(n, m)

# 검정 노드를 포함하는 모든 누텔라 찾기
for n in B:
    # 검정끼리는 L[m]이 0이므로 다 더함
    for m in E[n]:
        answer += L[find(m)]

print(answer)