구간 합 알고리즘 (1차원 배열)

구간 합 알고리즘은 1차원배열에서 i ~ k번째 사이의 값들의 합을 구하는데 사용한다. 단순히 for문을 사용하여 i~k사이의 값을 더해가면서 할 수도 있지만 이 경우 시간복잡도는 O(N)이다. 하지만 구간 합 알고리즘의 경우 O(1)성능을 가집니다.

즉, 구간 합은 합 배열을 이용해 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘이다.
이 알고리즘을 활용하기 위해서는 먼저 합 배열을 구해야 한다.

배열 A가 있을 때 합 배열 S는 다음과 같이 정의된다.
🔽 합 배열 S의 정의
S[i] = A[0] + A[1] + A[2]+ ... + A[i-1]+ A[i]


합 배열은 기존의 배열을 전처리한 배열이라고 생각하면 된다. 이렇게 합 배열을 미리 구해 놓으면 시간 복잡도가 O(N) → O(1)로 감소한다.


🔽 합 배열 표

인덱스	0	1	2	3	4	5
배열 A	1	2	3	4	5	6
합 배열 S	1	3	6	10	15	21

🔽 합 배열 S를 만드는 공식
S[i] = S[i-1] + A[i]


합 배열을 만들었다면 아래와 같이 구간 합을 쉽게 구할 수 있다.
🔽 합 배열 S를 만드는 공식
S[j] - S[i-1] → i에서 j까지의 구간 합

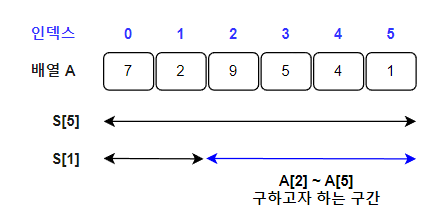
☄️A[2] ~ A[5] 까지의 구간합을 구하고자 한다. 어떻게 해야할까 ?

🔨 그림을 보고 이해가 되었다면 좋겠다. 정말 간단하게
A[0] ~ A[5]의 총 합을 S[] 배열에 저장하고 A[0], A[1]을 빼주면 되지 않을까 ? 과정을 한번 적어보자.

🔽 A[2] ~ A[5] 구간 합을 합 배열로 구하는 과정
S[5] = A[0] + A[1] + A[2] + A[3] + A[4] + A[5]
S[1] = A[0] + A[1]
S[5] - S[1] == A[2] + A[3] + A[4] + A[5]

🔽 코드로 구현해보자.

public class PrefixSum_example {
    public static void main(String[] args){
        int[] A =  {7, 2, 9 ,5, 4, 1}; // 배열 A
        int[] S = new int[A.length]; // 합 배열 S

       S[0] = A[0]; //첫 번째 요소는 그대로 복사

        // 합 배열 S를 만드는 공식 적용 → S[i] = S[i-1] + A[i]
        for(int i = 1; i<A.length; i++){
            S[i] = S[i-1] + A[i];
        }

        // 합 배열 S 출력
        for (int i = 0; i < S.length; i++) {
            System.out.println("S[" + i + "] = " + S[i]);
        }

        // 구간 합 구하는 공식 적용 → S[5] - S[2-1]
        System.out.println(S[5] - S[2-1]);
    }
}