합 배열 - 나머지 합 구하기

🔎 문제

N개의 수 A₁, A₂, ..., Aₙ이 주어졌을 때 연속된 부분의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램

즉, Aᵢ + ... + Aⱼ(i ≤ j)의 합이 M으로 나누어 떨어지는 (i, j)의 쌍의 개수를 구하기

입력 :
1번째 줄에 N과 M(1 ≤ N ≤ 10⁶ ≤ 2 ≤ M ≤ 10³),
2번째 줄에 N개의 수 A₁, A₂, ..., Aₙ이 주어진다.
(0 ≤ Aᵢ ≤ 10⁹)

출력 : 1번째 줄에 연속된 부분의 합이 M으로 나누어 떨어지는 구간의 개수 출력

예제 입력 1	예제 출력 1
5 3 1 2 3 1 2	7

🔍 문제 분석

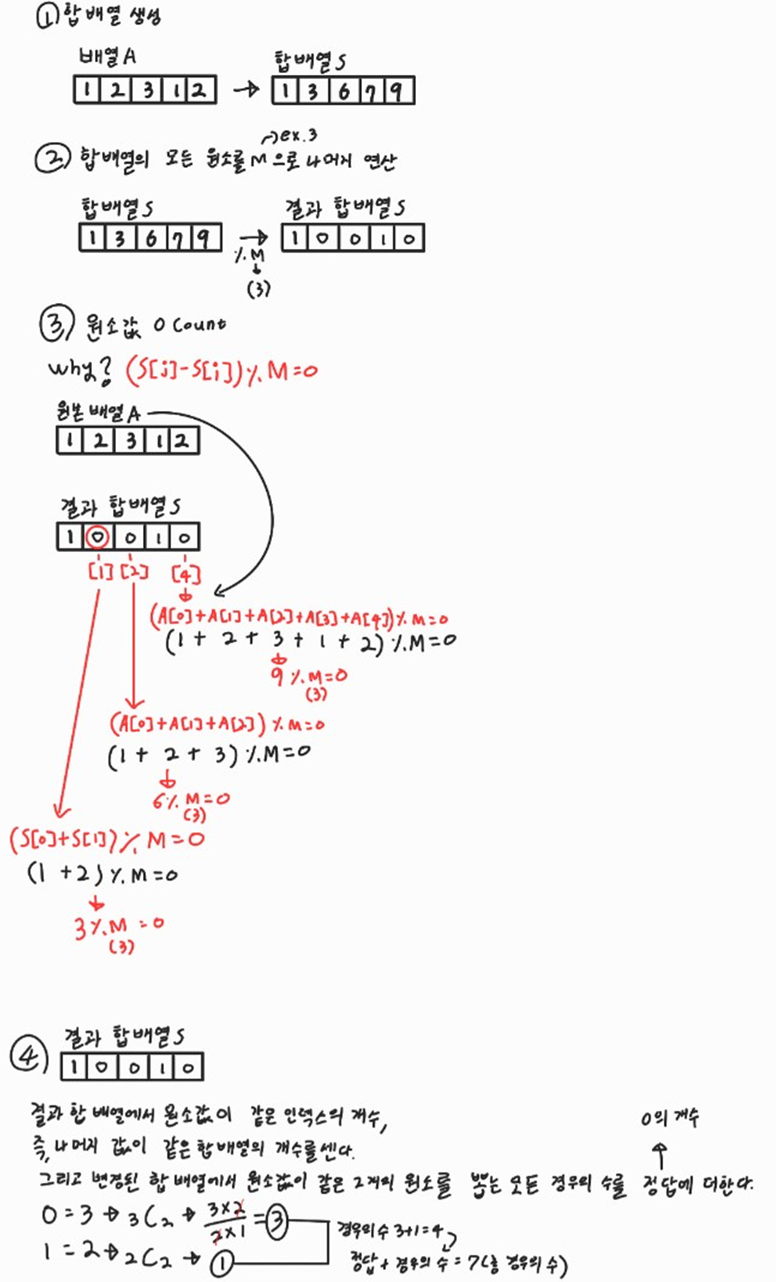
(1) 연속된 부분의 합 → 구간 합 배열을 사용

(2) Aᵢ + ... + Aⱼ(i ≤ j)의 합이 M으로 나누어 떨어지는 (i, j)의 쌍의 개수 → A 배열의 각 원소 중 M으로 떨어지는 원소들의 총 합을 구하기

(3) (A + B) % C == ((A % C) + (B % C)) % C,
❗ 특정 구간 수들의 나머지 연산을 더해 나머지 연산을 한 값과 구간 합의 나머지 연산을 한 값은 동일하다.

(4) S[j] % M의 값과 S[i] % M의 값이 같다면 (S[j]- S[i]) % M은 0이다.

합 배열 S를 만드는 공식 : S[i] = S[i-1] + A[i]

👀 코드

// TODO : 나머지 합 구하기

import java.io.IOException;
import java.util.Scanner;

public class BackJoon_10986 {
    public static void main(String[] args) throws IOException{
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int M = sc.nextInt();
        long[] S = new long[N];
        long[] C = new long[M];
        long answer = 0;

        // 합 배열 S 생성
        S[0] = sc.nextInt();
        for(int i = 1; i < N; i++) {
            S[i] = S[i-1] + sc.nextInt();
        }

        // 합 배열의 모든 값에 % 연산 수행
        for(int i = 0; i < N; i++) {
            int remainder = (int)(S[i] % M);
            // 0 ~ i 까지의 구간 합 자체가 0일 때 정답(asnwer)에 더하기
            if(remainder == 0)
                answer ++;
            // 나머지가 같은 인덱스의 개수 카운팅하기
            C[remainder]++;
        }

        for(int i = 0; i < M; i ++) {
            if (C[i] > 1) {
                // 경우의 수 구하기
                answer = answer + (C[i] * (C[i] -1) / 2);
            }
        }
        System.out.println(answer);
    }
}