3️⃣ 점근식 표기법

---

• 주어진 함수가 있을때, 보다 간단한 함수로 만들어 표시하는 방법
• 입력 데이터의 크기에 따라, 수행시간 혹은 사용공간이 얼마나 되는지를 객관적으로 비교할 수 있는 기준을 제시
• O(빅오), Ω(오메가), Θ(세타)
  
  
  
  

✅ Big-O : 상한표기법

---

• 정의

  $f(n) ≤ c*g(n)$

  • 모든 n (n≥k) 에 대해 f(n) ≤ c*g(n) 인 조건을 만족하는 c와 k가 존재하기만 하면 f(n) = O(g(n))이다
  • g(n)이 f(n)의 upper bound다
  • f(n)은 항상 g(n)보다 작다
  • f(n) 함수의 결과치가 g(n) 함수의 것보다 클 수 없다

• 예시

  $3n + 2 = O(n)$

  c > 0 이고 n ≥ 1 일때 (전제 조건) n ≥k 에 대해서 3n+2 ≤ c*n인 c, k가 존재하는가?

  ⇒ c = 5 , k=1 일때 true (존재)
  

• 연산 시간의 크기 순서 $O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(3^2) < O(2^n) < O(n!)$
  

✅ Big-Omega : 하한표기법

---

• 정의 $c*g(n) ≤ f(n)$
  • 모든 n (n≥k) 에 대해 c*g(n) ≤ f(n) 인 조건을 만족하는 c와 k가 존재하기만 하면 f(n) = Ω(g(n))이다
  • g(n)이 f(n)의 lower bound다
  • f(n)이 아무리 작아도, g(n)보다는 크다

✅ Big-Theta

---

• 정의 $c*g(n) ≤ f(n) ≤c*g(n)$
  • 모든 n (n≥k) 에 대해 c1g(n) ≤ f(n) ≤ c2g(n) 인 조건을 만족하는 c1, c2와 k가 존재하기만 하면 f(n) = Θ(g(n))이다

✅ 접근식 표기법 증명 예시

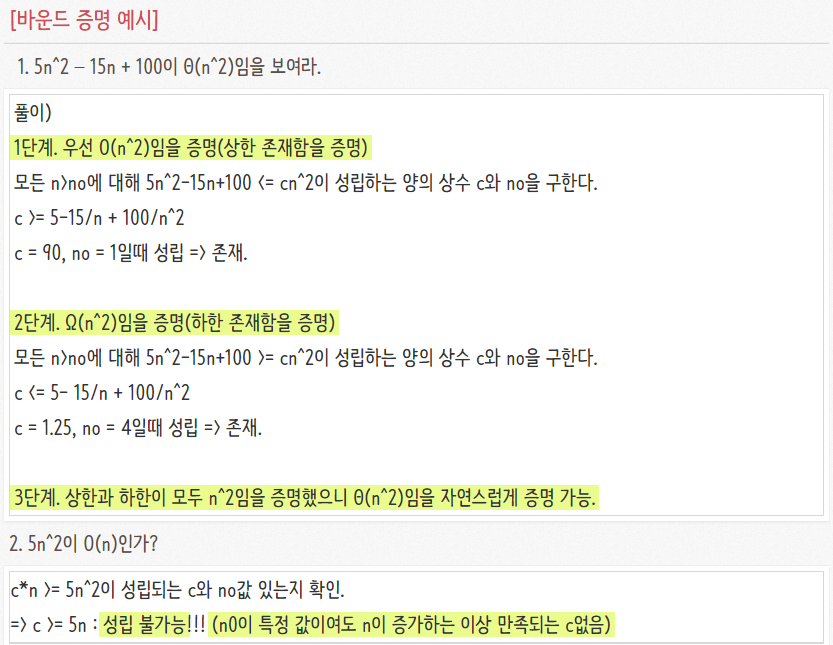
• 참고

알고리즘 이론 2강. 점근적 표기법(Asymptotic notation)