백준2775 문제 보러가기

문제

평소 반상회에 참석하는 것을 좋아하는 주희는 이번 기회에 부녀회장이 되고 싶어 각 층의 사람들을 불러 모아 반상회를 주최하려고 한다.

이 아파트에 거주를 하려면 조건이 있는데, “a층의 b호에 살려면 자신의 아래(a-1)층의 1호부터 b호까지 사람들의 수의 합만큼 사람들을 데려와 살아야 한다” 는 계약 조항을 꼭 지키고 들어와야 한다.

아파트에 비어있는 집은 없고 모든 거주민들이 이 계약 조건을 지키고 왔다고 가정했을 때, 주어지는 양의 정수 k와 n에 대해 k층에 n호에는 몇 명이 살고 있는지 출력하라. 단, 아파트에는 0층부터 있고 각층에는 1호부터 있으며, 0층의 i호에는 i명이 산다.

입력

첫 번째 줄에 Test case의 수 T가 주어진다. 그리고 각각의 케이스마다 입력으로 첫 번째 줄에 정수 k, 두 번째 줄에 정수 n이 주어진다

출력

각각의 Test case에 대해서 해당 집에 거주민 수를 출력하라.

제한

1 ≤ k, n ≤ 14

예제 입력 1

2
1
3
2
3

예제 출력 1

6
10

문제 해결

규칙 찾기

사실 지금 보면 간단한 문젠데, 6개월 전에 시도했을 때 모두 시간 초과로 어려움을 겪다가 포기한 문제다.

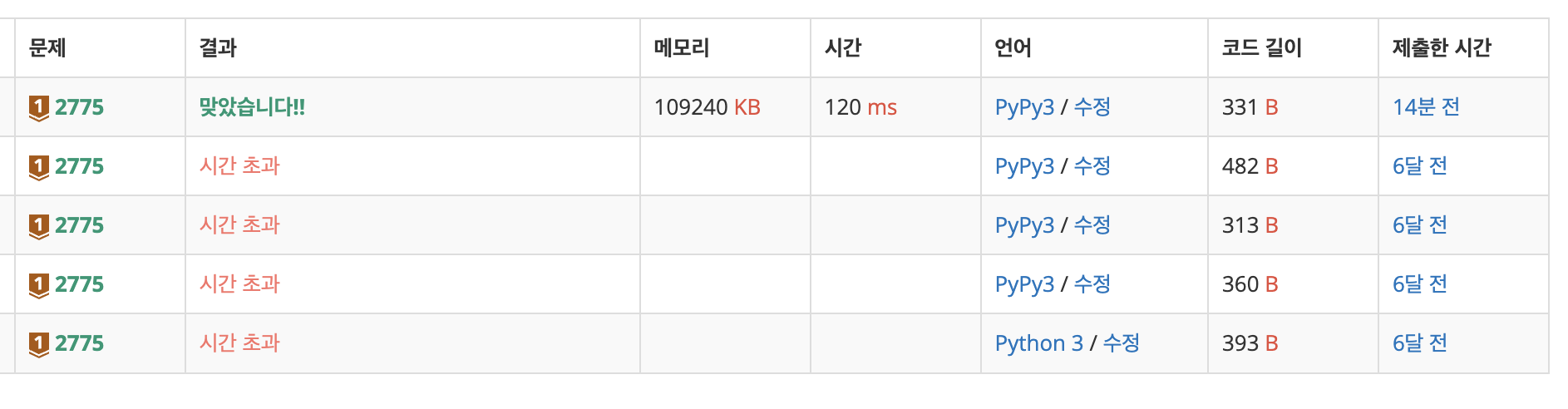
문제를 해석하면 다음과 같다.
예를 들어 3층의 6호를 알고 싶으면 다음과 같이 짜면 된다.

층/호	1호	2호	3호	4호	5호	6호
1층	1	2	3	4	5	6
2층	1	1+2 = 3	1+2+3 = 6	1+2+3+4 = 10	1+2+3+4+5 = 15	1+2+...+6 = 21
3층	1	1+3=4	1+3+6=10	1+3+6+10=20	1+3+6+10+15=35	1+3+6+10+15+21 = 46

규칙을 보면, 3층 6호를 계산하기 위해서 2층의 1호부터 6호까지 모두 더한 값이어야 한다.
그런데 보면 3층 5호가 이미 2층의 1호에서 5호까지 더한 값이기 때문에 3층의 5호에 2층의 6호를 더하면 된다.
그러면 코드는 다음과 같다.

T = int(input())

for _ in range(T) :
    k = int(input())
    n = int(input())
    
    dp = []
    for i in range(n) :
        dp.append(i+1) #0층 i호 명수 설정
    
    for i in range(1, k+1) :
        for j in range(n) :
            if j>0 :
                dp[j] += dp[j-1] # 현재 층 j호수 = 현재 층 j-1호수 + 전 층 j호수
            else :
                pass # 각 층의 1호는 무조건 1이기 때문에
            
    print(dp[n-1])