Routing protocols

Routing Prococols은 네트워크의 라우터를 통해 전송자로부터 수신자까지 아동하는 적절한 경로를 결정하는 프로토콜이다.

적절한 경로라는 말은 기준에 따라 다를 수 있다.
비용이 가장 적거나, 가장 빠르거나, congestion이 가장 적은 것일 수도 있다.
어떻게 적절한 경로를 결정할 것인가는 곧 전체 네트워크의 성능을 정하므로 매우 중요하다.

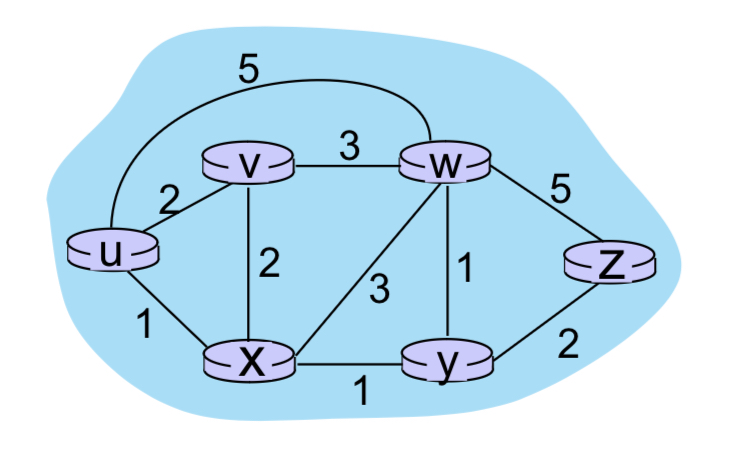
위와 같이 각각의 라우터를 노드로, 라우터를 연결하는 link들을 간선으로 추상화할 수 있다.

라우팅을 수행하는 라우팅 알고리즘을 두 가지로 분류할 수 있다.

• global
  모든 라우터가 전체 네트워크의 topology와 link cost에 대한 정보를 모두 가지고 있는 형태를 의미한다.
  -> link state 알고리즘 사용

• decentralized
  각각의 라우터가 자신과 이웃한 라우터까지의 link cost 정보만을 가지고 있고, 라우터들 간의 정보 교환을 통해 점차 link cost 정보를 확장, 갱신해 나가는 형태를 의미한다.
  -> distance vector 알고리즘 사용

Link State Algorithm

모든 라우터들의 network topology와 link cost를 알고 있다.
그래프 탐색 알고리즘 중 다익스트라 알고리즘을 이용한다.

다익스트라 알고리즘은 그래프에서 특정 노드부터 다른 모든 노드들까지의 최단거리를 구할 수 있는 알고리즘이다.

다익스트라 알고리즘은 n번의 iteration마다 추가한 노드의 이웃 간선 정보를 추가하는 과정을 거치기 때문에 O(n^2)의 시간 복잡도로 알려져 있고, 개선을 통해 O(nlogn) 만에 수행 가능하다.

Distance Vector Algorithm

각 노드는 자신에게 연결된 이웃의 링크의 비용만 알고 있기 때문에 이웃 노드들끼리 반복적으로 정보를 교환해 최적의 경로를 갱신한다.
벨만-포드 알고리즘을 주로 이용한다.

각 노드가 인접한 노드들의 routing table을 보고 자신이 가진 routing table을 갱신하는 과정을 가진다.
다익스트라 알고리즘이 이웃들 간의 '간선 정보'만을 참조한다면 벨만 포드 알고리즘은 routing table 전체를 교환한다고 볼 수 있다.

만약에 자신이 갖고 있는 노드 간의 경로보다, 나의 이웃으로부터 새롭게 받은 정보의 경로가 더 좋은 경로라면 이를 수정한다. 그리고 수정 사항이 생겼으면 나의 이웃들이 내가 알고 있는 경로를 참조하고 있을 수 있으므로, 나의 이웃들에게 또 다시 수정본 routing table 정보를 보내준다. 만약 수정사항이 생기지 않았으면 정보를 보내지 않는다.

위와 같은 작업을 가지기 때문에, Distance Vector 알고리즘은 반복적이고 비동기적이다.

Count-to-infinity problem

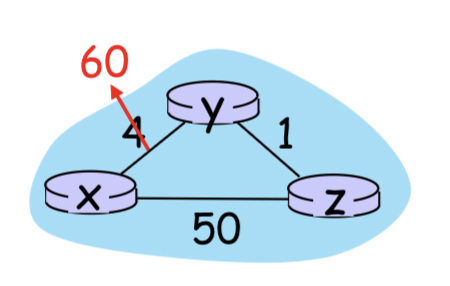
count to infinity 란, distance vector 알고리즘에서 나타날 수 있는 문제점이다.

위 사진과 같은 구조로 간선 정보가 존재하고, 각 노드들은 자신의 distance vector를 완성하여 가지고 있다고 가정할 때, 간선 (x,y)의 비용이 4에서 60까지 증가했다고 가정한다.

• y는 z의 distance vector를 이용하여 x까지의 비용을 수정한다. (z의 DV에는 간선 비용 변경 전의 z->y->x 경로, 즉 비용 5짜리의 경로가 존재)
• y->z 까지의 거리가 1이고, z의 DV에 따르면 z->x 까지의 거리가 5이므로 y는 x까지의 비용을 6으로 수정한다. (y->x->x 경로)
• 변경사항이 발생했으므로 y는 자신의 DV를 x와 z에게 전달한다.
• 이를 받은 z는 거리르 재연산한다. z에서 x까지 직접 가는 z->x 경로보다 y를 경유하여 z->y->x 가 더 비용이 적다. y의 DV에 따르면 y->z 경로 비용은 6이므로, 여기에다가 z->y 경로를 더하여 7을 x까지의 경로로 수정한다. (z->y->x)

위의 작업이 계속 반복되어 y->x 정보가 8로, z->x 정보가 9로 변한다. 불필요한 연산이 많이 수행되고 나면 y에서 x로 가는 비용이 51임을 알 수 있다. 그리고 이 단계를 거치면 z에서 y를 거쳐서 x로 가는 것보다 x로 바로 가는 것이 더 비용이 적다.

이는, 어떤 간선의 정보가 이웃 간의 DV가 아닌 외부에 의해 변경 되었을 때, 노드들끼리 갖고 있는 예전 정보를 반복적으로 참조하면서 발생한다.

LS vs DV algorithm

• message complexity
  LS : n개의 라우터가 있다고 하면, O(n^2) 메시지 교환
  DV : 이웃 간의 교환으로 수렴 시간이 항상 동적

• speed of convergence
  LS : O(n^2)
  DV : 무한대가 될 수도 있음(count-to-infinity problem으로 인해)

• 정보
  LS : 모든 정보를 인식하고 있음
  DV : 이웃한 라우터의 정보만을 인식

• 사용 알고리즘
  LS : 다익스트라 알고리즘
  DV : 벨만-포드 알고리즘

• 교환 방식
  LS : 링크 정보만을 교환
  DV : 전체 라우팅 테이블을 교환

• 라우팅 테이블
  LS : 내 라우팅 테이블을 다른 노드가 참조하지 않음
  DV : 내 라우팅 테이블을 다른 노드가 참조함