백준2225 문제 보러가기

문제

0부터 N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 구하는 프로그램을 작성하시오.

덧셈의 순서가 바뀐 경우는 다른 경우로 센다(1+2와 2+1은 서로 다른 경우). 또한 한 개의 수를 여러 번 쓸 수도 있다.

입력

첫째 줄에 두 정수 N(1 ≤ N ≤ 200), K(1 ≤ K ≤ 200)가 주어진다.

출력

첫째 줄에 답을 1,000,000,000으로 나눈 나머지를 출력한다.

예제 입력 1

20 2

예제 출력 1

21

예제 입력 2

6 4

예제 출력 2

84

문제 해결

규칙 찾기

다른 dp 문제와 비슷하게 현재 상황에 영향을 주는 이전 상황과 관련된 규칙을 찾는 것이 나의 목표였다.
예를 들어, N이 6이고, K가 3이라고 생각해보자. 경우는 다음과 같다.

0 0 6 0 1 5 0 2 4 0 3 3 0 4 2 0 5 1 0 6 0 / 1 0 5 1 1 4 1 2 3 1 4 1 1 5 0 / ... / 6 0 0

규칙이 보이는가?
6,3 일 경우에는 6 2 6 1 6 0 일 때의 경우를 모두 합한 것이다. 왜냐하면 각 경우에서 맨 앞자리를 뺸다고 생각하면 다음과 같다.

(0) 0 6 (0) 1 5 (0) 2 4 (0) 3 3 (0) 4 2 (0) 5 1 (0) 6 0 / (1) 0 5 (1) 1 4 (1) 2 3 (1) 4 1 (1) 5 0 / ... / (6) 0 0

이렇게 되면 6,2 / 6,1 / 6,0 일 경우와 같다. (K=0이 될 수 없지만 점화식을 위해서 설정했다.)
표를 작성하면 다음과 같다.

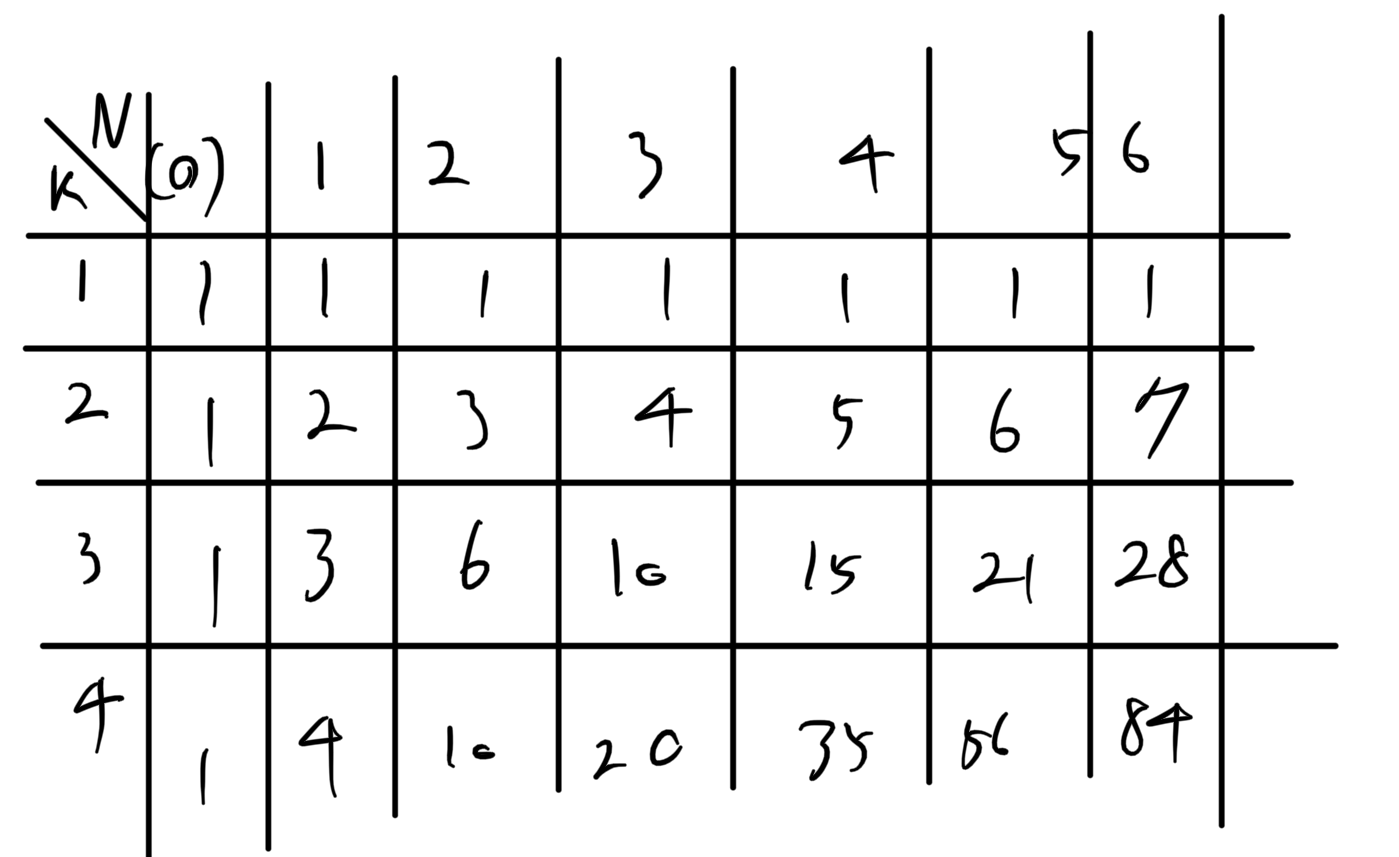
다음과 같이 표현할 수 있다.
점화식은 dp[i] = dp[i-1] + dp[i] 와 같이 된다.

코드는 다음과 같다.

N, K = map(int, input().split())

dp = [1]*(N+1)

for i in range(K-1) :
    for j in range(N+1) :
        if j == 0 :
            dp[j] = 1
        else :
            dp[j] = dp[j-1] + dp[j]
            
print(dp[N]%1000000000)```