실행시간 T(N) = running times(수행 횟수)
- 함수나 알고리즘 수행에 필요한 스탭의 수로 계산한다.
- 임의의 함수가 N이 무한대일 때, 어떤 함수 형태에 근접해지는지 분석을 점근적 분석으로 실행 시간을 계산한다.
N이 무한대라면 → 상수(b), 최고차항 계수(a) 의미가 없고 최고차항(N)만 의미가 있다. - input N의 크기에 영향을 받는다.
점근적 표기법
- 최단 시간 실행 - Ω(1)
최장 시간 실행 - O(N)
** 일반적으로 빅오 표기법을 가장 많이 사용한다. - tight bound - θ(N) : 하한선과 상한선의 값이 동일할 때
예제 ) 이진 탐색 시간 복잡도 구하기
N * (1/2)^k = 1
N = 2^k
logN = log2^k
logN = klog2
logN = k
θ(logN)
O(1)
입력값(N)이 증가해도 실행시간은 동일
시간 복잡도 → 기본 연산 수라고 생각
ex) stack의 push, popn = [0] if n[0] == 1: print(true) else: print(false)
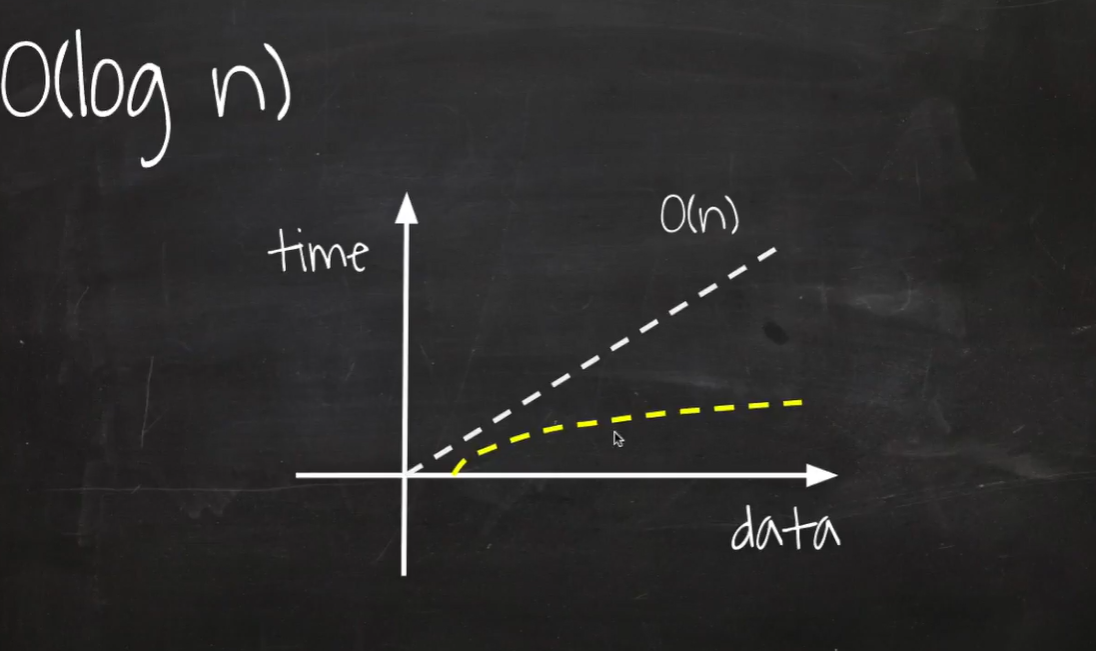
O(logN) - binary search
연산이 한 번 실행될 때 마다 데이터의 크기가 절반 감소하는 알고리즘 (log의 지수는 항상 2)
ex) binary search 알고리즘, tree 형태 자료구조 탐색
O(n)
입력값(N)이 증가함에 따라 실행시간도 선형적으로 증가
ex) 1중 for문for i in range(n): print(i)
O(NlogN)
O(N)의 알고리즘과 O(log N)의 알고리즘이 중첩된 형태
ex) 퀵 / 병합 / 힙 정렬
O(n^2)
ex) 2중 For 문, 삽입/거품/선택 정렬
for i in range(n): for j in range(n): print(i+j)
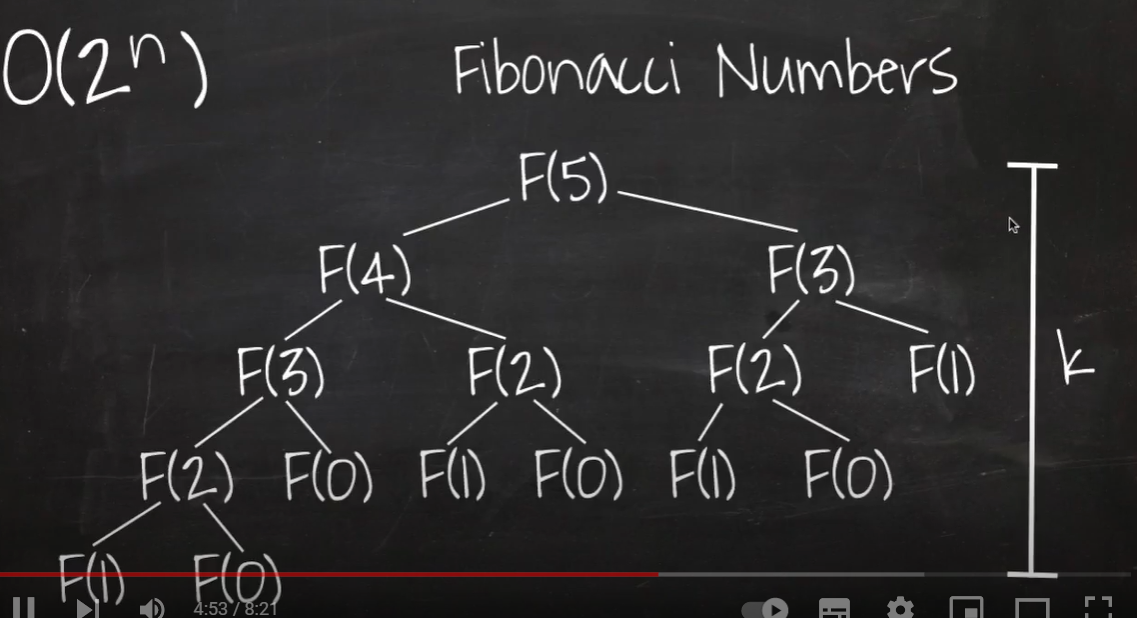
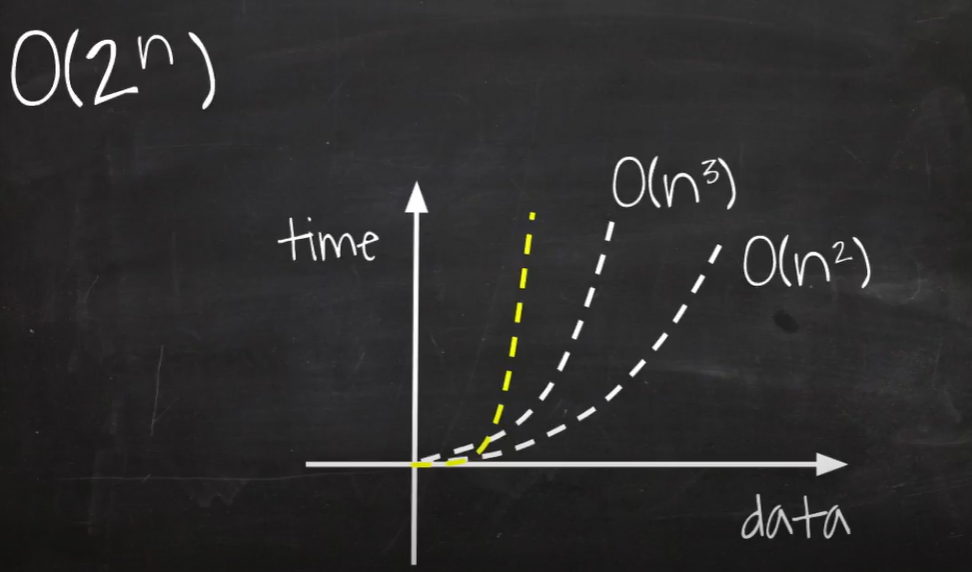
O(2^n)
빅오 표기법 중 가장 느린 시간 복잡도로 주로 재귀적으로 수행하는 알고리즘이 이에 해당
ex) fibonacci 수열def fibonacci(n,r): if n <= 0: return 0 else: if n == 1: return r[n] = 1 f(n-1, r) + f(n-2, r)
💡알고리즘 문제 풀 때 Tip
입력 데이터의 범위와 실행 시간 범위를 고려하면 문제에 대한 감을 잡을 수 있다. 보통 코드 1억 번 수행시간은 1초이다. 이를 기준으로 전체 수행시간을 어림잡아 문제에 사용되는 알고리즘에 대한 힌트를 얻으면 알고리즘 사용 가능 여부를 판단하여 접근할 수 있다.
위 근사치를 이용하면 간단하게 입력의 크기와 제한시간으로 정답 알고리즘의 복잡도를 대략적으로나마 예측해 볼 수 있습니다.
문제에서 가장 먼저 확인해야하는 내용은 시간제한(수행시간 요구사항)입니다.
시간제한이 1초인 문제를 만났을 때, 일반적인 기준은 다음과 같습니다.
- 입력이 10,000,000 개의 경우: O(N) 알고리즘
- 입력이 50,000 개인 경우: O(N * log N) 알고리즘
- 입력이 10,000 개인 경우: O(N * N) 알고리즘
- 입력이 400개: O(N N N) 알고리즘
거꾸로 이야기하면 입력이 100개 이하라면 대체로 어떤 알고리즘을 써도 풀릴 가능성이 높고, 입력이 매우 작은 경우는 완전탐색으로도 문제를 풀 수 있을 가능성이 높다는 이야기겠죠.
정렬 알고리즘 비교
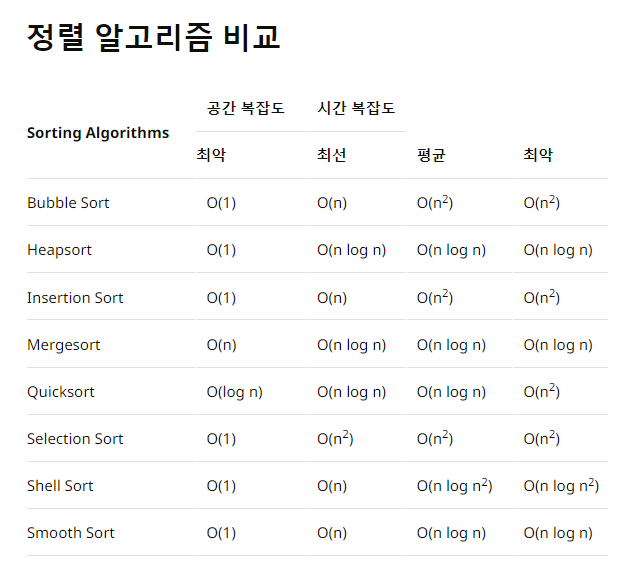
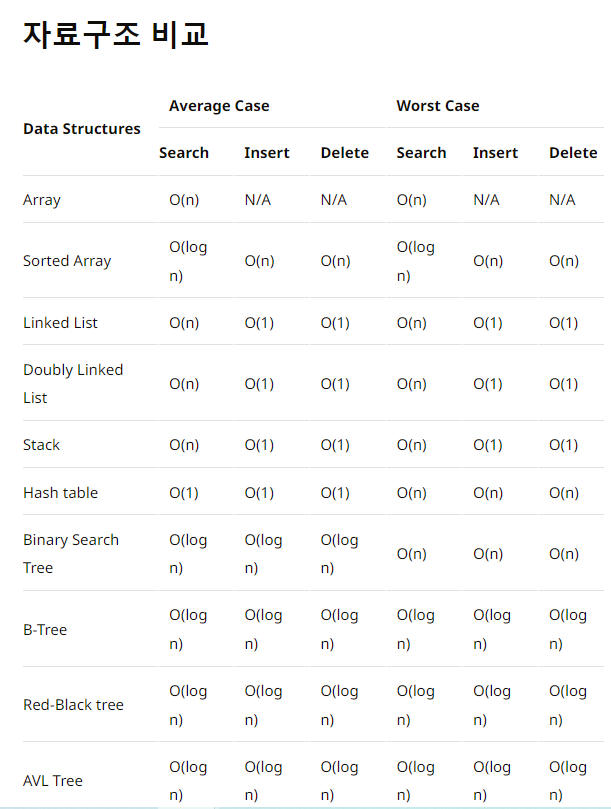
자료구조 비교